Table of Contents |
Up until now, we only integrated functions that were above the x-axis on 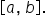 We’ll use this example to see what happens when that is not the case.
We’ll use this example to see what happens when that is not the case.
Consider the function 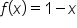 on the interval
on the interval 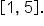
The graph on the left is  on the interval
on the interval 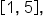 and the graph on the right shows the rectangles that could be used in a Riemann sum. Remember, the rectangles have a base on the x-axis and extend out to the graph of
and the graph on the right shows the rectangles that could be used in a Riemann sum. Remember, the rectangles have a base on the x-axis and extend out to the graph of  .
.
|

|
Now consider a Riemann sum, 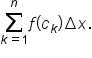
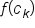 is positive, we know the quantity
is positive, we know the quantity 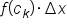 is the area of one rectangle.
is the area of one rectangle. 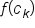 is negative, the quantity
is negative, the quantity 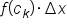 is the negative of the area of that one rectangle.
is the negative of the area of that one rectangle. Now, consider the definite integral of this function on the interval 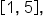 written
written 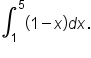
We know the value of this integral is the limit of the Riemann sums as the number of rectangles gets larger and larger 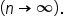
Note that the area of the region between  and the x-axis is
and the x-axis is 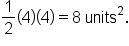
Then, 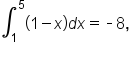 the negative of the area of the region.
the negative of the area of the region.
 is below the x-axis on
is below the x-axis on 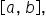 then
then 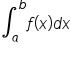 is the negative of the area of the region between
is the negative of the area of the region between  and the x-axis on
and the x-axis on 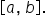
EXAMPLE
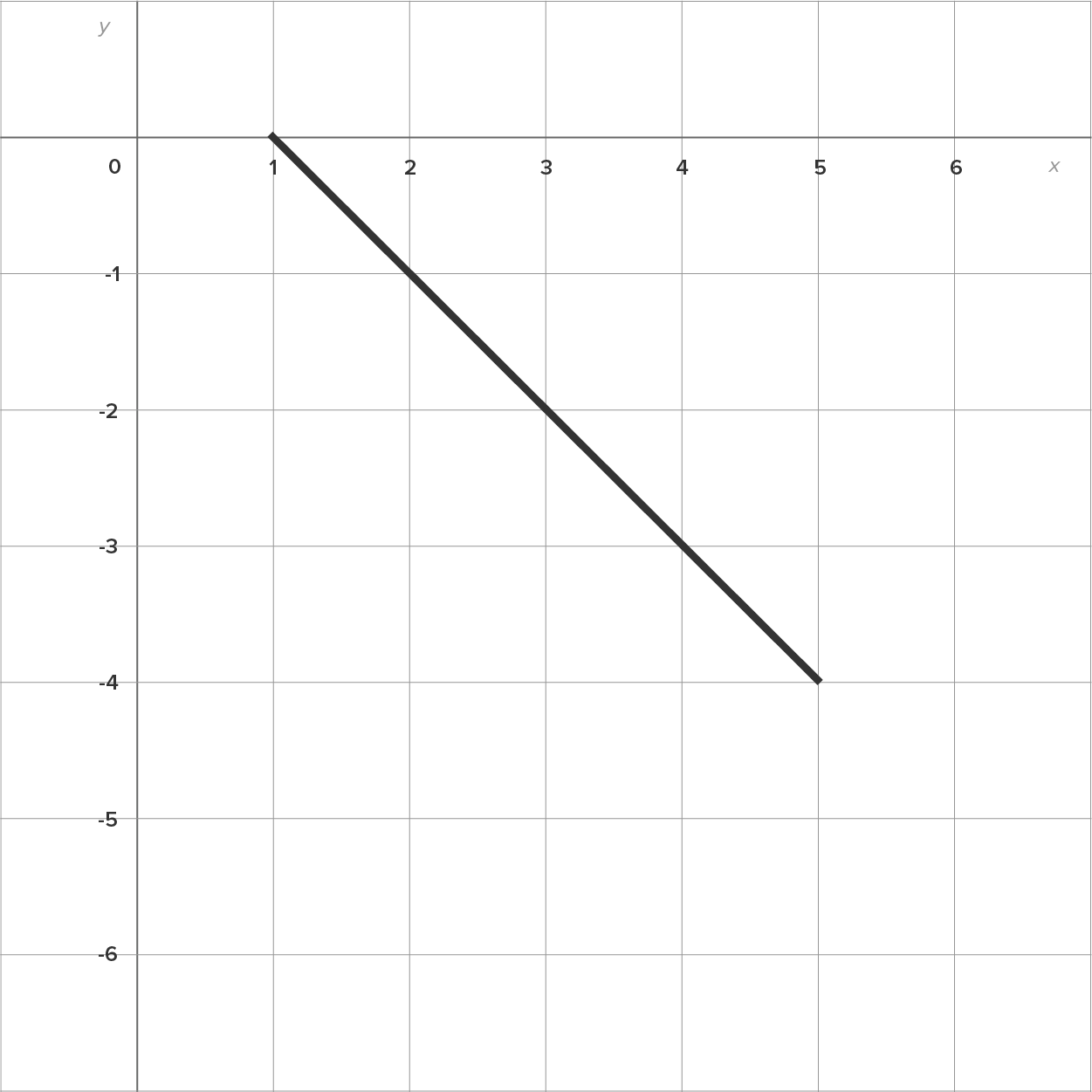
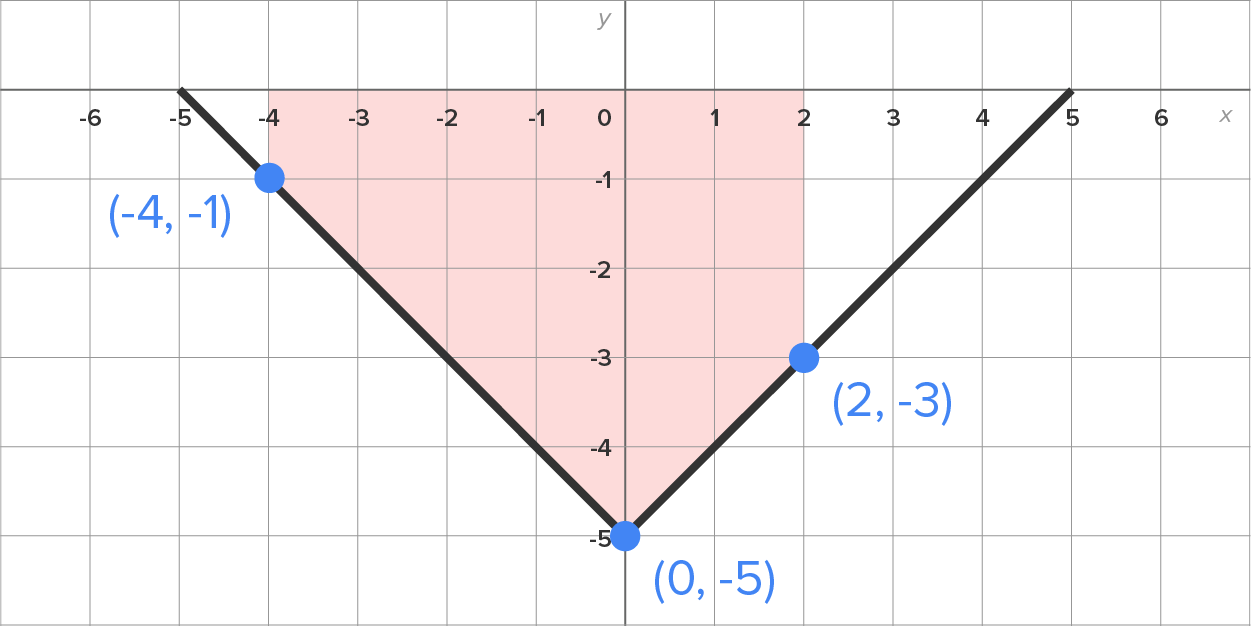
Evaluate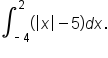
 is shown on the left and the region is shown on the right.
is shown on the left and the region is shown on the right.
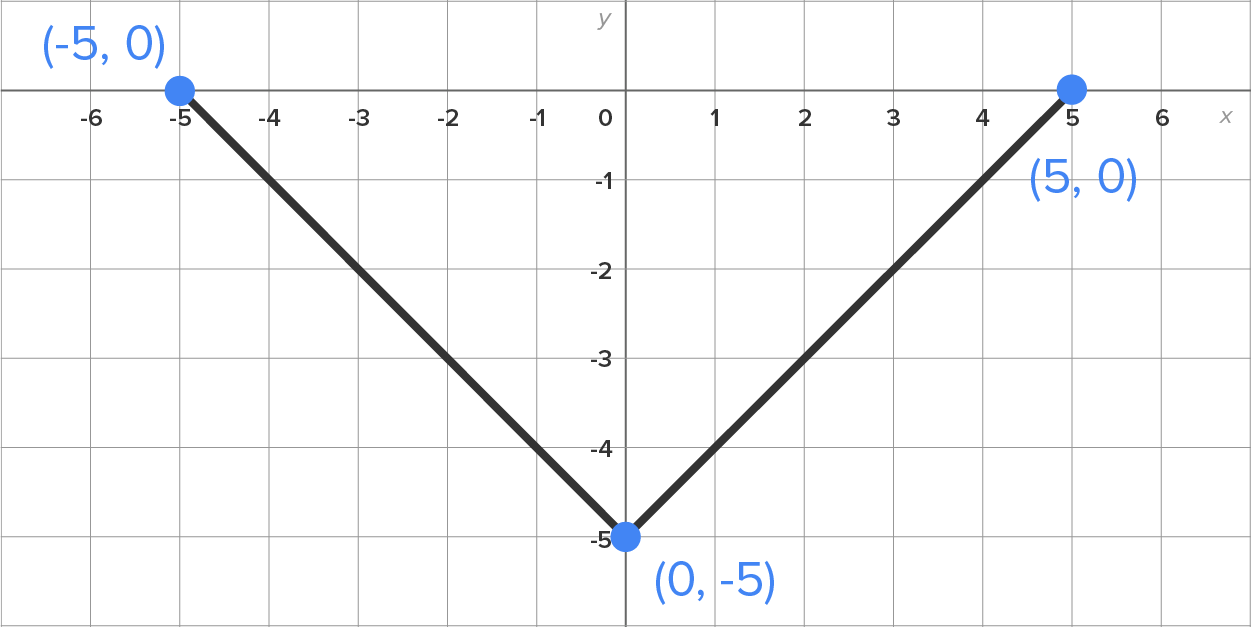
|
|
 is below the x-axis on the interval
is below the x-axis on the interval 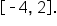 The region itself is not a standard shape, so let’s split the region at
The region itself is not a standard shape, so let’s split the region at 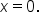
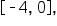 the region is a trapezoid with parallel (vertical) bases 1 and 5, and (horizontal) height 4. The area is
the region is a trapezoid with parallel (vertical) bases 1 and 5, and (horizontal) height 4. The area is 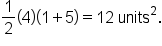
 the region is a trapezoid with parallel (vertical) bases 5 and 3, and (horizontal) height 2. The area is
the region is a trapezoid with parallel (vertical) bases 5 and 3, and (horizontal) height 2. The area is 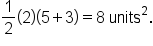
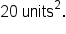
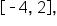
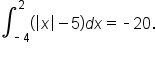
Suppose we wish to evaluate 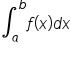 for the function whose graph is shown in the figure.
for the function whose graph is shown in the figure.
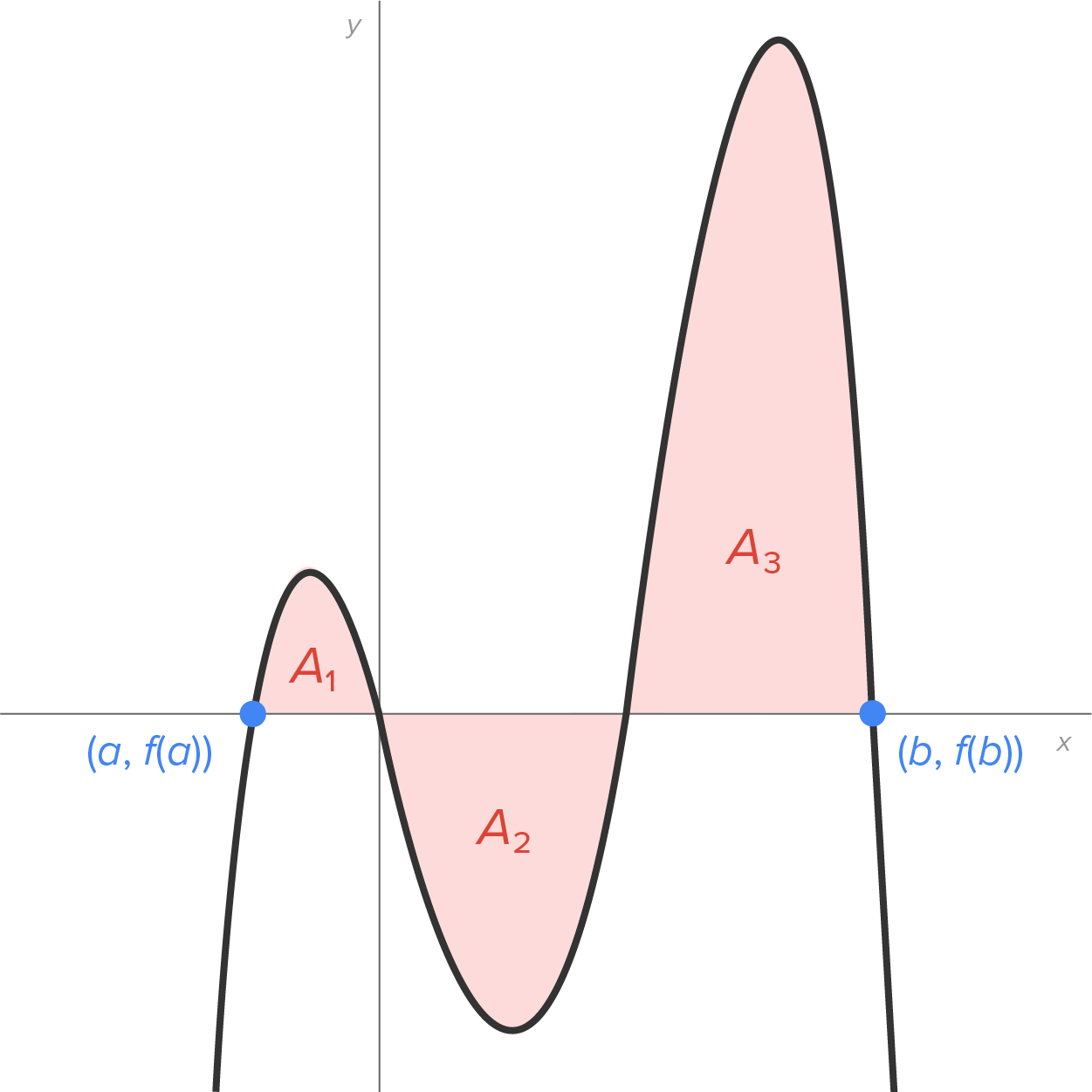
Notice how this region is broken into 3 smaller regions with areas 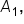
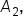 and
and 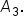
Now, consider the definite integral on 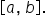
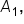 the definite integral is equal to
the definite integral is equal to 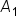 since the region is above the x-axis.
since the region is above the x-axis. 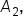 the definite integral is equal to
the definite integral is equal to 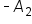 since the region is below the x-axis.
since the region is below the x-axis. 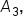 the definite integral is equal to
the definite integral is equal to 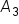 since the region is above the x-axis.
since the region is above the x-axis. 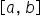 is equal to the sum of the three definite integrals, or
is equal to the sum of the three definite integrals, or 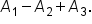 In general, we would add any area above the x-axis and subtract any area below the x-axis.
In general, we would add any area above the x-axis and subtract any area below the x-axis.
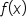 takes on both positive and negative values on
takes on both positive and negative values on 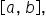 then:
then: 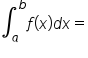 (sum of all areas above the x-axis) - (sum of all areas below the x-axis)
(sum of all areas above the x-axis) - (sum of all areas below the x-axis)Let’s look at an example.
EXAMPLE
Evaluate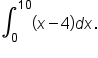
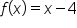 on the interval
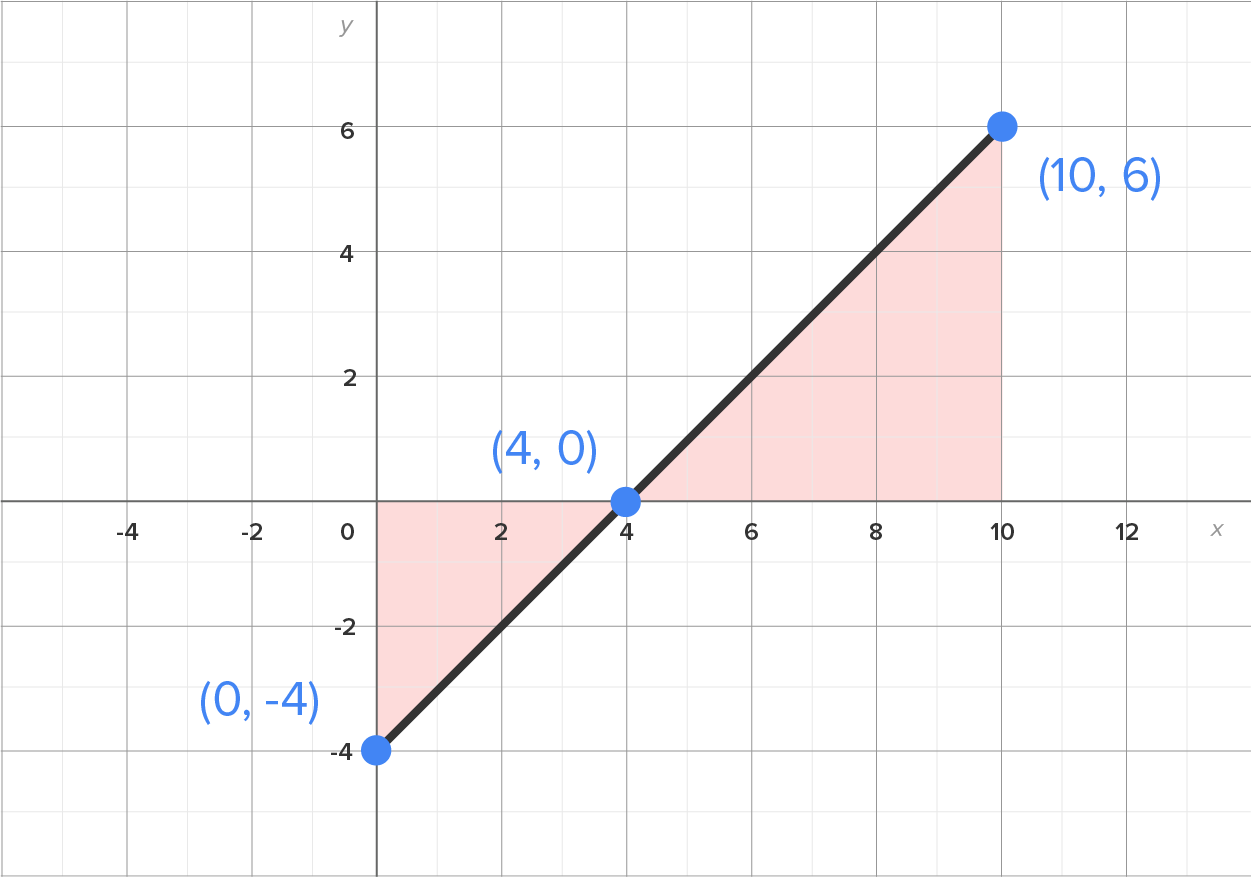
on the interval 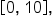 as shown in the figure on the left. The figure on the right shows the graph with the relevant regions.
as shown in the figure on the left. The figure on the right shows the graph with the relevant regions.

|
|
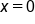 and
and  has area
has area 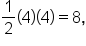 and is below the x-axis.
and is below the x-axis.
 and
and 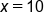 has area
has area 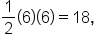 and is above the x-axis.
and is above the x-axis.
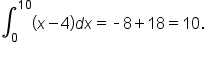
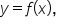 we’ll find
we’ll find 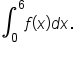
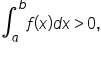 there is more area above the x-axis than below the x-axis on
there is more area above the x-axis than below the x-axis on 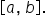
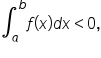 there is more area below the x-axis than above the x-axis on
there is more area below the x-axis than above the x-axis on 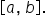
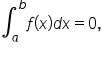 there is as much area above the x-axis as there is below the x-axis on
there is as much area above the x-axis as there is below the x-axis on 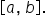
 as shown in the figure below that can be used to evaluate
as shown in the figure below that can be used to evaluate 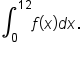

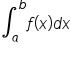 when the graph of f(x) is below the x-axis. You applied this knowledge in evaluating definite integrals when f (x) ≤ 0 on [a, b]. Lastly, you learned that when evaluating definite integrals when f (x) is both negative and positive on [a, b], you can interpret the value of the definite integral as “net area,” considering regions that are above and below the x-axis. This will be very useful when investigating applications in the next tutorial.
when the graph of f(x) is below the x-axis. You applied this knowledge in evaluating definite integrals when f (x) ≤ 0 on [a, b]. Lastly, you learned that when evaluating definite integrals when f (x) is both negative and positive on [a, b], you can interpret the value of the definite integral as “net area,” considering regions that are above and below the x-axis. This will be very useful when investigating applications in the next tutorial.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 4 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.