Table of Contents |
Variables can be classified into two data types: quantitative and categorical. A quantitative variable is one that measures/contains values about a numerical quantity or amount. A categorical variable, sometimes called a qualitative variable, classifies people, objects, or units into categories. The table below provides some rules of thumb for differentiating between quantitative and categorical variables.
| What Type of Variable Is It? | |
|---|---|
| Quantitative Variable | Categorical Variable |
|
Think “how much” or “how many.” The average makes sense. |
Think “who/what is being classified.” The average does not make sense. |
For quantitative variables, think “numbers.” A quantitative variable tells you how much or how many of some quantity you have, and the average will make sense. Imagine you added up all the values of a quantitative variable column and divided them by the total number of observations you have; would that result (average) make sense?
For a categorical variable, think “categories/levels.” Does the variable classify people, objects, and units into categories? It should not make any sense to take an average of a categorical variable.
EXAMPLE
The table below shows some transactional data for a retail company.
There are three measurement levels for quantitative data; continuous, ratio, and discrete. A measurement level describes the scale of the variable. The measurement level lets you know what type of mathematical operation is appropriate for the variable. For example, can an average value be computed, or is another measure more appropriate? A continuous measurement level means the variable's value can take on any value in an interval. Continuous measurement levels can contain decimals. A ratio measurement level contains all the characteristics of a continuous measurement level with the additional aspect of a true zero point. Meaning zero represents the absence of the value. For example, a salary of $0 represents no income. Zero inventory represents no items. A profit margin of 0% means no profit. Contrast the meaning of a zero value for a continuous measurement level. For example, temperature that is measured in Fahrenheit or Celsius degrees. Zero degrees Fahrenheit does not mean “no temperature;” it is just a reference point. A discrete measurement level means the variable’s value cannot take on a value in an interval. Discrete measurement levels are integers; they cannot take decimal values.
Returning to the retail data shown in the table below, Sales Revenue has a continuous measurement level because sales can take on a value in an interval. For example, the company could have earned $50,000.50. This is a viable value for Sales Revenue. The Number of Customers has a discrete measurement level because the company cannot have 300.5 customers. You cannot viably have half a person. The Number of Customers variable is measured in integers only and cannot take on a value in an interval.
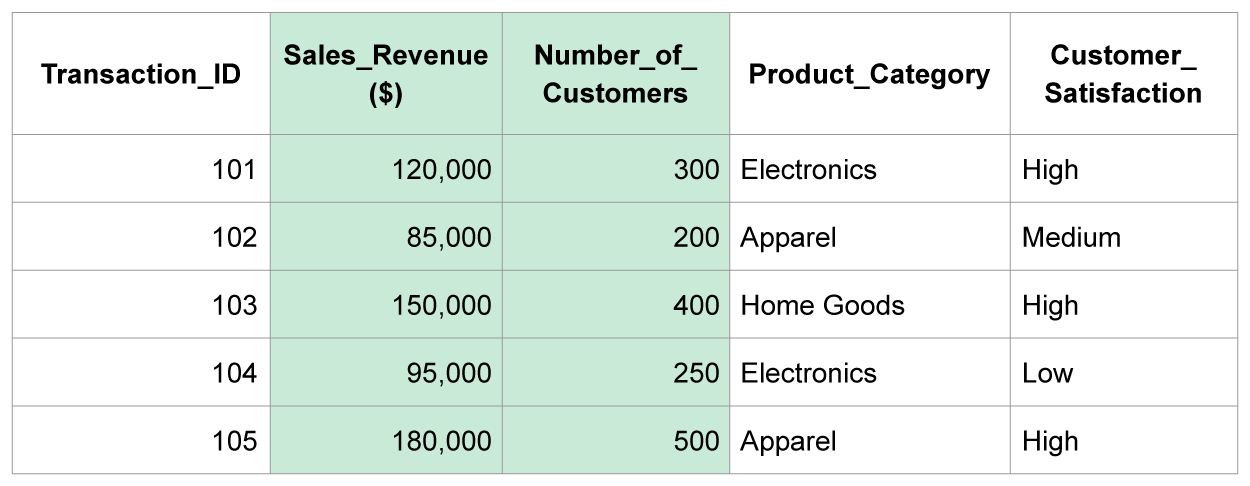
| Variables with Continuous Measurement Levels | Variables with Discrete Measurement Levels |
|---|---|
|
|
There are two measurement levels for categorical data; nominal and ordinal. A nominal measurement level means the categories have no natural order to them. Whereas, at an ordinal measurement level, the categories do have a natural order to them. Using the retail data again, you can see in the table below that the variable Product Category is nominal. The categories "Electronics," "Apparel," etc. are simply labels for the items sold, and there is not one category that is "naturally higher" than another. Electronics is not higher or better than Apparel.
Customer satisfaction is an ordinal variable. An ordinal variable refers to a type of data where the categories have a natural order or ranking, but the distances between the categories are not meaningful. In the case of Customer Satisfaction, this means that we can order responses (e.g., “very dissatisfied,” “neutral,” “very satisfied”) from lowest to highest. Ordinal measurement levels are common in surveys and rating scales, where the order matters.

| Variables by Measurement Level | |
|---|---|
| Nominal | Ordinal |
|
|
Knowing your data type and the associated measurement levels is important because it impacts the types and number of analytical methods you can apply. You can use more analytical methods with quantitative data than you can with categorical data.
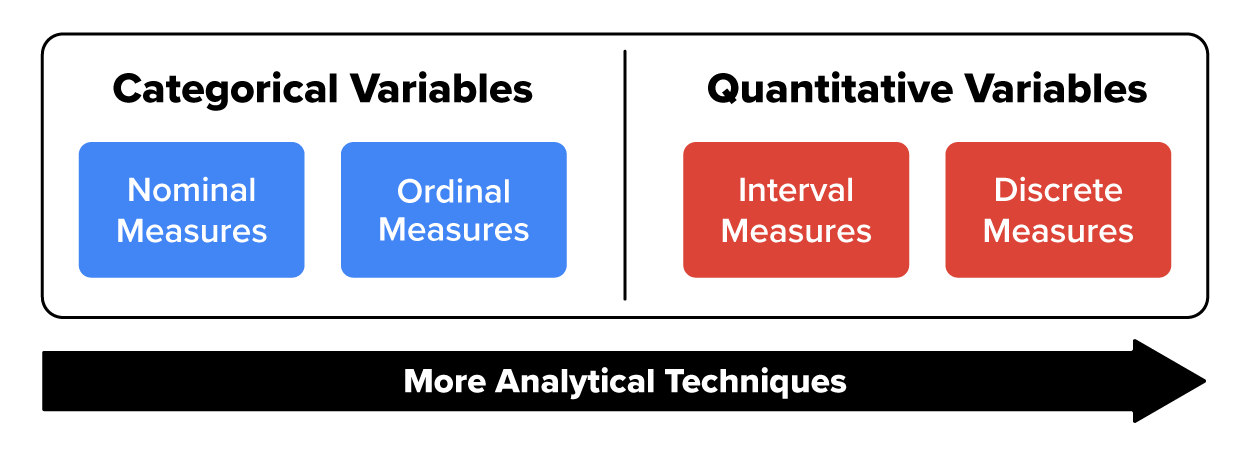
The table below shows the different types of analytical methods that can be used based on the measurement level of the variables. For interval and discrete measurement level data, you have more analytical methods at your disposal.
| Nominal | Ordinal | Interval | Discrete | |
|---|---|---|---|---|
| Mode | yes | yes | yes | yes |
| Median | no | yes | yes | yes |
| Mean | no | no | yes | yes |
| Standard Deviation | no | no | yes | yes |
By recognizing the data type and its measurement level, you can choose the appropriate statistical technique, create appropriate visualizations, and draw meaningful insights from your data. If you do not recognize the appropriate data type and measurement level, the results from your analysis will have unintended consequences. Consider the scenario below.
IN CONTEXT
You are working for an online retailer. The company wants to conduct a customer satisfaction survey about a new fast checkout process on their mobile app. The company collects feedback on a scale from 1 (very dissatisfied) to 5 (very satisfied). The customer feedback data is ordinal because the scale of the data (1 to 5) has an order to the values. Suppose you have 100 customer responses.
You treat the customer satisfaction scores as continuous data and take the average of the values as follows:
- 50 customers provide a rating of 5 (very satisfied).
- 50 customers provide a rating of 1 (very dissatisfied).
You report an average of 3 but realize this does not make sense because it implies a moderate satisfaction level, which contradicts the extreme ratings (1 and 5) given by customers. Managers might wrongly assume everything is fine based on the neutral sentiment. However, the average does not reflect the large number of customers who are very dissatisfied.
The average calculation provided is not correct because the average ignores the ordinal nature of the data. The difference between each rating level is not uniform. Going from “neutral” (3) to “satisfied” (4) may not represent the same change in satisfaction as going from “dissatisfied” (2) to “neutral” (3).
A better approach to understanding this data would be to construct a visualization like a column chart shown below that shows the distribution of the customer ratings.
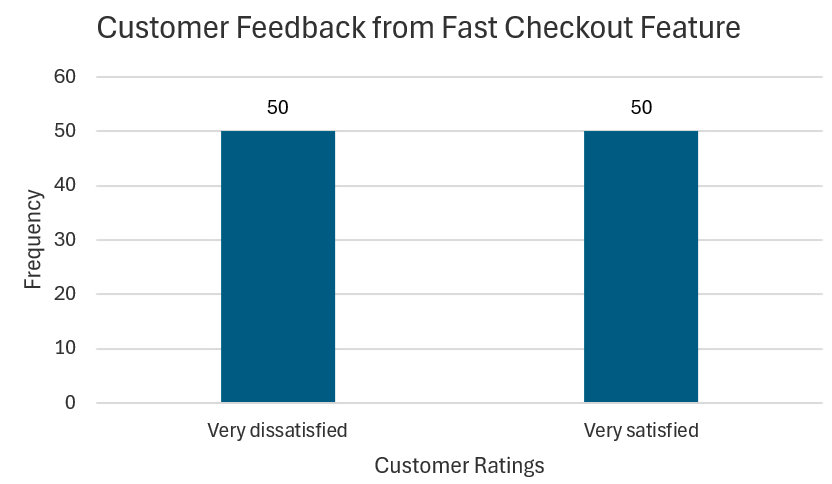
You will learn how to create a column chart like this one in the next tutorial. Understanding data type and measurement level ensures meaningful analysis and prevents misleading conclusions!
Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.