EXAMPLE
GizmoHub is a small e-commerce business that sells the latest tech gadgets, including smartphones, tablets, and accessories. The store has been operating for a year, and the management is keen to understand its revenue patterns better to make informed decisions about inventory, marketing, and financial planning.
The management at GizmoHub has noticed that their daily revenue varies significantly due to factors like promotions, holidays, and market trends. They want to estimate the average monthly revenue to plan their budget and set realistic sales targets for the upcoming year. However, the variability in daily revenue makes it challenging to predict monthly revenue accurately.
You are a business data analyst at GizmoHub. You decide to construct a full Monte Carlo simulation with 1,000 simulations to estimate the average monthly revenue. This approach provides a more thorough and reliable estimate of potential monthly revenues for GizmoHub.
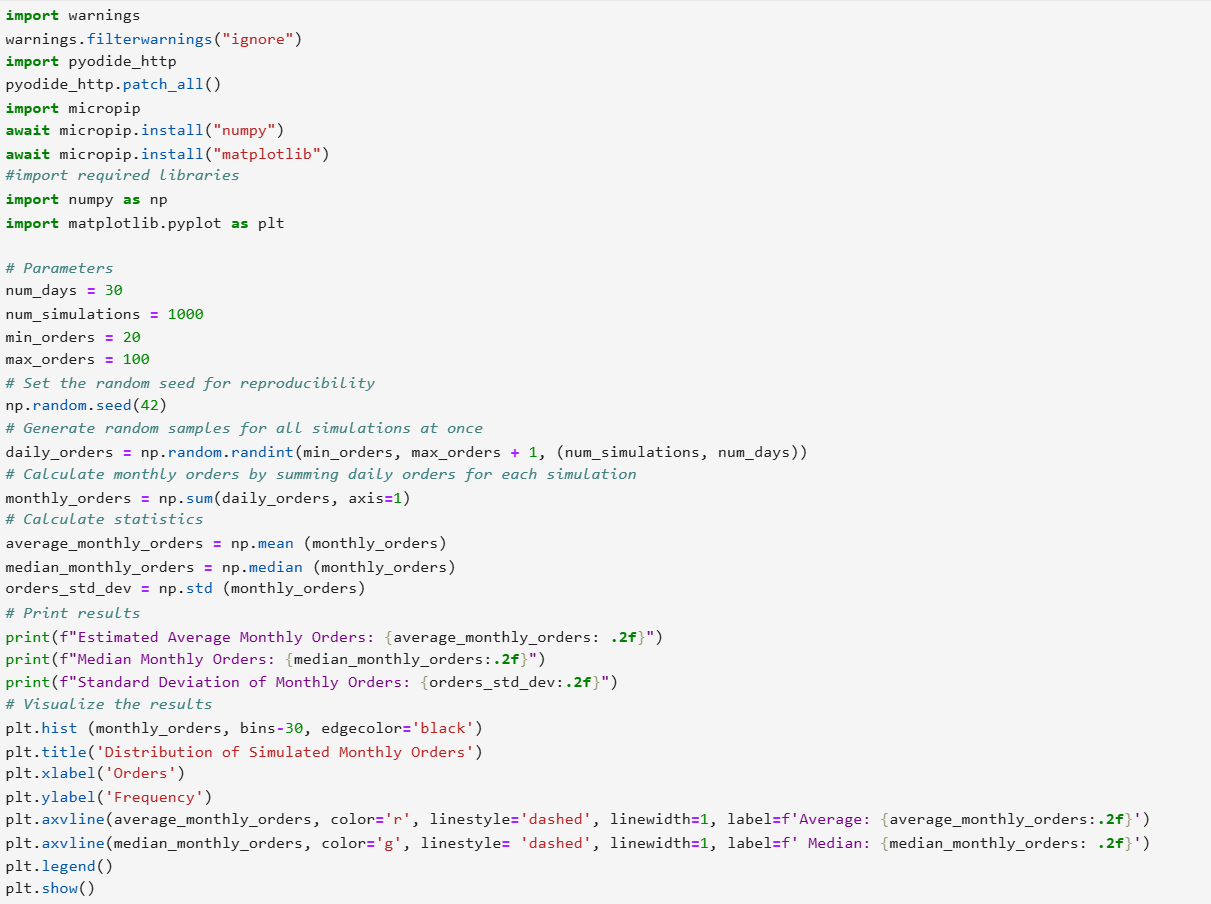
The code below installs and imports the necessary libraries and performs a full Monte Carlo simulation. This code runs the Monte Carlo simulation 1000 times, generating a range of possible monthly revenues. It then calculates and prints the average, median, and standard deviation of the simulated monthly revenues, and visualizes the distribution. The output from the Monte Carlo simulation is also provided.
It is important to note that the code that sets up the environment by importing pyodide_http for internet requests and installing essential packages (numpy and matplotlib) using micropip is missing from the screenshot below but is required before you run the code shown in the screenshot.

Let’s break down the code to understand how you can implement the Monte Carlo simulation.
Step 1: Define the Problem
GizmoHub, a small e-commerce business specializing in tech gadgets, wants to better understand their revenue patterns to make informed decisions about inventory, marketing, and financial planning. The management has observed significant variability in daily revenue due to factors such as promotions, holidays, and market trends. To plan their budget and set realistic sales targets for the upcoming year, they need to estimate the average monthly revenue.
In this context, the random variable is the daily revenue, which can vary between $200 and $1,000. The outcome of interest is the average monthly revenue, which will help GizmoHub account for the variability in daily revenue and provide a range of possible outcomes for better decision-making.
Steps 2 and 3: Determine the Probability Distribution and Generate Random Samples

np.random.seed(42)
- This line sets the random seed to 42, ensuring that the random numbers generated are the same each time the code is run.
num_days = 30
num_simulations = 1000
min_revenue = 200
max_revenue = 1000
- The lines above define the parameters of the Monte Carlo simulation. They help set up the environment in which the simulation runs and determine the range of the random variables involved.
daily_revenues = np.random.randint(min_revenue, max_revenue + 1, (num_simulations, num_days))
- This line generates random daily revenues for all simulations at once. It creates a 2D array where each row represents a simulation, and each column represents a day. The values are randomly chosen between $200 and $1,000.
Step 4: Perform the Simulations

monthly_revenues = np.sum(daily_revenues, axis=1)
- This line calculates the monthly revenue for each simulation by summing the daily revenues. The axis=1 argument ensures that the sum is calculated across the columns (days) for each row (simulation).
average_monthly_revenue = np.mean(monthly_revenues)
median_monthly_revenue = np.median(monthly_revenues)
revenue_std_dev = np.std(monthly_revenues)
-
average_monthly_revenue: Calculates the average monthly revenue across all simulations.
-
median_monthly_revenue: Calculates the median monthly revenue across all simulations.
-
revenue_std_dev: Calculates the standard deviation of the monthly revenues, indicating the variability.
print(f"Estimated Average Monthly Revenue: ${average_monthly_revenue:.2f}")
print(f"Median Monthly Revenue: ${median_monthly_revenue:.2f}")
print(f"Standard Deviation of Monthly Revenue: ${revenue_std_dev:.2f}")
- These lines print the calculated statistics, providing an estimate of the average, median, and standard deviation of the monthly revenues.
Step 5: Analyze the Results

plt.hist(monthly_revenues, bins=30, edgecolor='black')
plt.title('Distribution of Simulated Monthly Revenue')
plt.xlabel('Revenue ($)')
plt.ylabel('Frequency')
plt.axvline(average_monthly_revenue, color='r', linestyle='dashed', linewidth=1, label=f'Average: ${average_monthly_revenue:.2f}')
plt.axvline(median_monthly_revenue, color='g', linestyle='dashed', linewidth=1, label=f'Median: ${median_monthly_revenue:.2f}')
plt.legend()
plt.show()
-
plt.hist: Creates a histogram to visualize the distribution of the simulated monthly revenues.
-
plt.title: Sets the title of the histogram.
-
plt.xlabel: Labels the x-axis as "Revenue ($)."
-
plt.ylabel: Labels the y-axis as "Frequency."
-
plt.axvline: Adds vertical dashed lines to indicate the average and median monthly revenues on the histogram.
-
plt.legend: Adds a legend to the histogram.
-
plt.show: Displays the histogram.
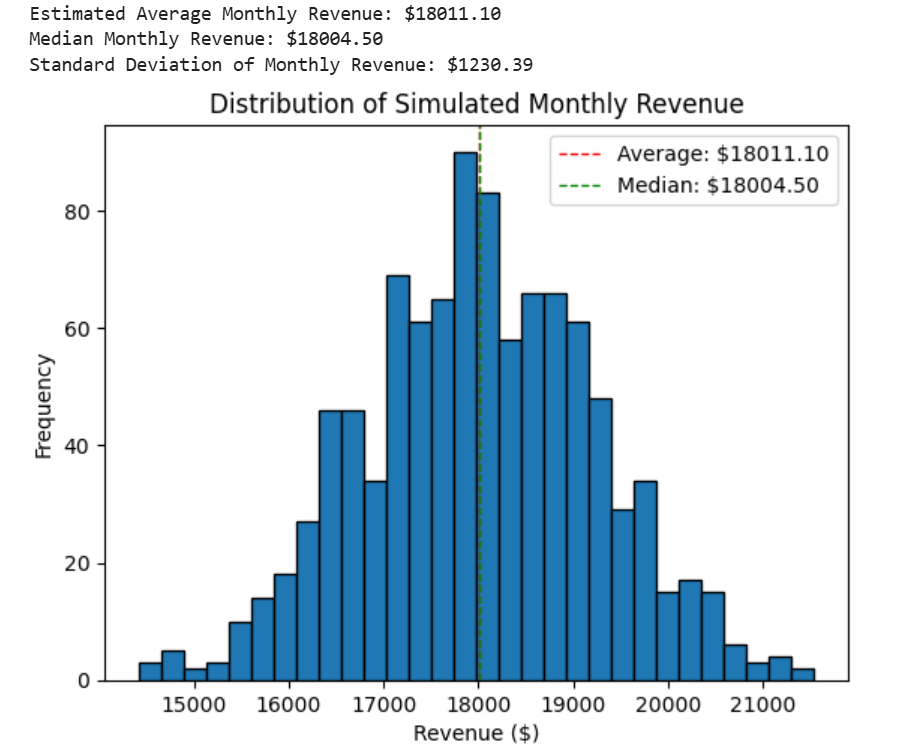
The histogram visualizes the distribution of the simulated monthly revenues from the full Monte Carlo simulation using 1,000 simulated daily revenue values. Here’s what it shows:
-
Frequency Distribution: The x-axis represents the range of monthly revenues, while the y-axis represents the frequency (how often each revenue range occurs across the simulations).
-
Average Monthly Revenue: A red dashed line indicates the average monthly revenue across all simulations.
-
Median Monthly Revenue: A green dashed line indicates the median monthly revenue across all simulations.
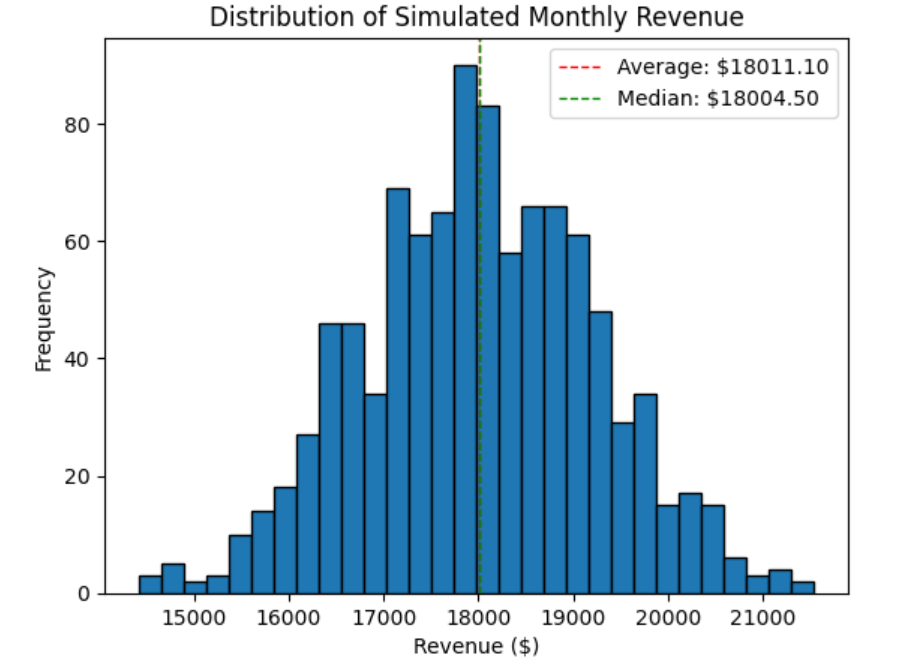 Step 6: Interpret the Results
Interpretation of the Average and Median Revenue Values from the Full Monte Carlo Simulation
Step 6: Interpret the Results
Interpretation of the Average and Median Revenue Values from the Full Monte Carlo Simulation:
Average Monthly Revenue
The average monthly revenue (mean) is calculated by summing all the simulated monthly revenues and dividing by the number of simulations. In the context of GizmoHub, the average monthly revenue provides an estimate of what the typical monthly revenue might be, considering the variability in daily revenues due to factors like promotions, holidays, and market trends.
-
Context: For GizmoHub, the average monthly revenue helps the management understand the expected revenue over a month, considering the range of possible daily revenues. This figure is useful for budgeting, financial planning, and setting sales targets.
Median Monthly Revenue
The median monthly revenue is the middle value of the simulated monthly revenues when they are sorted in ascending order. It represents the point at which half of the simulated monthly revenues are below and half are above.
-
Context: For GizmoHub, the median monthly revenue provides an estimate that is less affected by extreme values (outliers) compared to the average. This is particularly useful if there are occasional very high or very low daily revenues that could skew the average. The median gives a more robust measure of the central tendency of the monthly revenues.
Practical Implications
-
Budgeting and Financial Planning: Both the average and median monthly revenues help GizmoHub set realistic budgets and financial plans. The average gives a general expectation, while the median provides a more stable estimate.
-
Sales Targets: Understanding both metrics allows GizmoHub to set achievable sales targets. The average helps in setting optimistic targets, while the median ensures that targets are realistic and not overly influenced by outliers.
-
Risk Management: By considering both the average and median, GizmoHub can better manage financial risks. The average helps in understanding the overall expected revenue, while the median provides a safeguard against extreme variations.
In summary, the average monthly revenue gives a general expectation of monthly revenue, while the median monthly revenue provides a more stable estimate that is less influenced by outliers. Both metrics are crucial for making informed decisions about inventory, marketing, and financial planning at GizmoHub.
Interpretation of the Standard Deviation from the Full Monte Carlo Simulation:
The standard deviation of $1,230.39 in the context of GizmoHub's Monte Carlo simulation represents the variability or dispersion in the simulated monthly revenues. This value provides insight into how much the monthly revenues are expected to fluctuate around the average monthly revenue.
Practical Implications
-
Revenue Fluctuations: The standard deviation indicates that the monthly revenues can vary by approximately $1,230.39 from the average monthly revenue. This helps GizmoHub understand the extent of revenue fluctuations they might experience, due to factors like promotions, holidays, and market trends.
-
Risk Management: By knowing the standard deviation, GizmoHub can better prepare for months with lower-than-average revenues. This information is crucial for managing financial risks and ensuring that the business can sustain operations even during less profitable months.
-
Inventory and Staffing Decisions: The variability in monthly revenues can impact inventory and staffing needs. For example, during months with higher revenues, GizmoHub might need more inventory and staff to handle increased demand. Conversely, during months with lower revenues, they might need to adjust inventory orders and staffing levels to avoid excess costs.
In summary, the standard deviation of $1,230.39 provides GizmoHub with valuable insights into the variability of their monthly revenues. This information is essential for making informed decisions about inventory, staffing, and risk management, ultimately helping the business operate more efficiently and sustainably.