Table of Contents |
Total cost is one factor used to determine the profitability of a firm. A firm’s total cost depends on the production decision. This decision involves determining the quantities of inputs the firm uses to produce its output and the cost of those inputs to the firm. The production function tells the firm what combinations of inputs are needed to produce a specific quantity of output, and it establishes the total cost of production.
EXAMPLE
Duangjan is opening a pop-up shop to sell her Japanese street fashion inspired clothing and accessories for children. She received her first shipment of clothing today. The cost of production was a bit more than Duangjan had estimated. She is now worried about making a success of her business. Will she make enough to cover her costs?When determining total costs, every input used in production must be counted. Explicit costs include payments to the owners of the factors of production that a firm purchases for use in production of its good or service. These are easy to track, as there will be sales receipts. Owners of resources are paid compensation: land receives rent, labor receives wages, capital receives interest, and entrepreneurship receives profit.
As you learned in the lesson on economic profit, every resource used by a business has a cost. If a business uses but does not compensate the owner of the resource with payment, then a value must be assigned. Uncompensated inputs have an implicit cost. Implicit cost represents the nonmonetary opportunity cost of using a resource for business purposes. The opportunity cost of working for yourself is what you would have earned if you had pursued your next best option instead self-employment.
EXAMPLE
Jon works as a grocery delivery driver using his own vehicle. While the grocery delivery company compensates Jon for his time, it is unlikely the wear and tear on the car is fully compensated. The depreciation of the vehicle is an implicit cost.Recall that production costs are categorized by whether the input is fixed or variable in the short run. Recall that inputs that cannot be easily increased or decreased in the short run are fixed costs, and inputs that can be easily increased or decreased in the short run are variable costs.
In our example of C&C Family Farm, a small business firm producing strawberries, we determined that the firm has fixed inputs: the 10 year lease on the 20 acres of land, which costs $5,000 to rent, and its capital equipment, the tractor and wagon. Fixed costs are spent, and cannot change due to contracts and leasing agreements. We will assume that the firm does not purchase additional capital equipment during the short run. C&C Family Farm’s variable input is the number of workers the firm hires on a daily basis. Labor has a variable cost, because labor can be easily increased or decreased in the short run.
To determine production costs for C&C Family Farm, we collect information on the fixed and variable costs. In the following table, notice that the fixed cost (FC) is $100 per day. The fixed cost stays the same for all levels of output. Even when no output is produced, the firm still has fixed costs. Review column 4 in the table to confirm. The variable cost (VC) will change, depending on how many workers are hired to produce a specific amount of output. We will assume that each worker is paid $100 per day.
The variable cost in column 3 is calculated by multiplying the number of workers in the row by the $100 daily wage. When no workers are hired, the variable cost is zero dollars. The first worker is paid $100 for the day. The variable cost is $100 ($100 * 1 worker). Notice in column 3 that the variable cost rises as more workers are hired.
|
Total Output (Pounds) (1) |
Labor (Workers) (2) |
Variable Cost (VC = $100 per day per worker) (3) |
Fixed Cost ($100) (4) |
|---|---|---|---|
| 0 | 0 | $100 * 0 = $0 | $100 |
| 100 | 1 | $100 * 1 = $100 | $100 |
| 230 | 2 | $100 * 2 = $200 | $100 |
| 290 | 3 | $100 * 3 = $300 | $100 |
| 350 | 4 | $100 * 4 = $400 | $100 |
| 380 | 5 | $100 * 5 = $500 | $100 |
| 400 | 6 | $100 * 6 = $600 | $100 |
| 390 | 7 | $100 * 7 = $700 | $100 |
If we sum the fixed and variable input costs, we can determine the total cost for producing the various levels of output. Notice in the table below that when we produce no output, the total cost (column 3) is $100 ($0 for variable cost + $100 for fixed cost). Even when C&C Family Farm is not picking strawberries, fixed costs are present. The lease must be paid, and the interest on capital equipment loan must be paid. As the level of output increases, the total cost rises as a result of increasing variable cost.
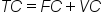
|
Fixed Cost (FC = $100) (1) |
Variable Cost (VC = $100 per day per Worker) (2) |
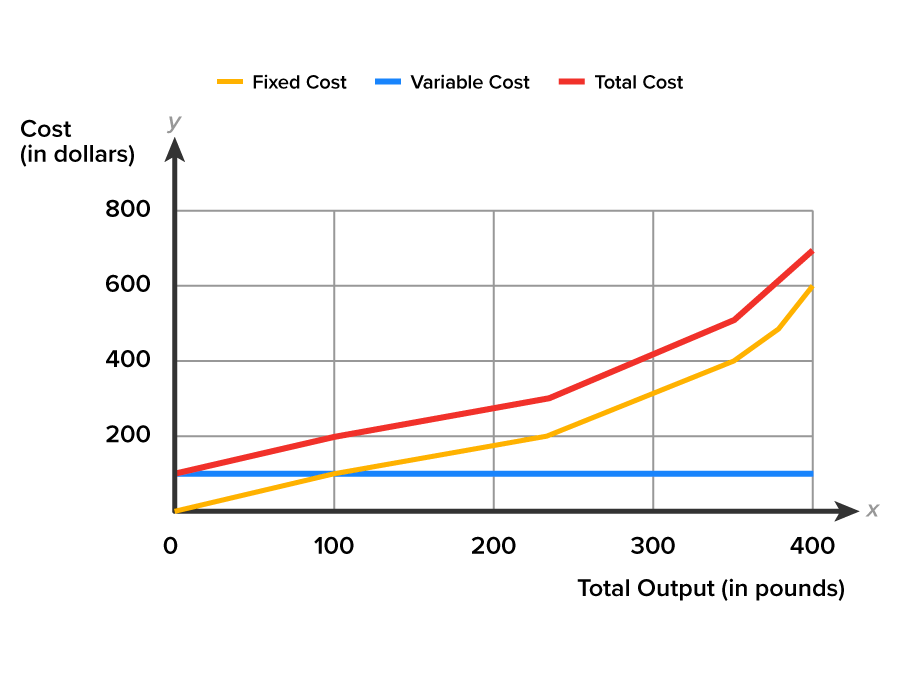
Total Cost (TC = FC + VC) (3) |
|---|---|---|
| $100 | 0 | $100 |
| $100 | 100 | $200 |
| $100 | 200 | $300 |
| $100 | 300 | $400 |
| $100 | 400 | $500 |
| $100 | 500 | $600 |
| $100 | 600 | $700 |
| $100 | 700 | $800 |
The following graph plots the production cost information against total output for C&C Family Farm. This graph will make it easier to confirm our observations about fixed costs, variable costs, and total cost.
In the graph below, notice that the fixed cost curve (blue) is horizontal. Fixed cost remains the same, whether the firm produces zero units of output or 400 units. For this reason, the blue line representing fixed cost is horizontal at $100 dollars. Also, notice that the yellow line representing variable costs begins at zero (because no workers have been hired), and rises as the level of output increases and more workers are hired. The red line representing total cost (the sum of fixed and variable costs) lies above both the fixed and variable cost lines, beginning at $100 and running parallel to the variable cost line–as expected.
Costs can be measured in several ways, including total, fixed, variable, and marginal. Each provides the firm with insights into its operations. Sometimes firms need to look at their cost per unit of output, and not just their total cost. There are two ways to measure per unit cost. Per unit cost can be measured as an average or a margin. We will review marginal cost in the next tutorial. In this tutorial we will explore three types of average costs.
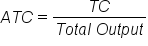
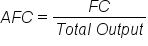
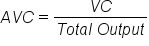
Consider the information on the costs of production in the table below. The table includes the formulas for TC, AVC, AFC, and ATC, along with data and the results of the calculations. Notice that ATC has no entry in the first row, where zero total output is produced. Why? Because we do not divide by zero. In row two of the table, the average total cost of producing 100 pounds of strawberries is $2.00 per pound ($200 / 100 pound). Producing 230 pounds results in a decrease in the per unit cost to $1.30, after which per unit cost increases. Notice that in column 6 of the table, the AFC decreases as the level of output increases. This is to be expected. The $100 of fixed cost is being spread over more and more units of output as production increases. Column 5 of the table reports the average variable cost. Notice that AVC begins at $1.00 per unit, falls, then begins to rise again. This is a pattern similar to what happens with average total cost (column 7).
|
Total Output (Pounds) (1) |
Variable Cost (VC=$100 per Day per Worker) (2) |
Fixed Cost (FC=$100) (3) |
Total Cost (TC=FC+VC) (4) |
Average Variable Cost (AVC=VC/Total Output) (5) |
Average Fixed Cost (AFC=FC/Total Output) (6) |
Average Total Cost (ATC=TC/Total Output) (7) |
|---|---|---|---|---|---|---|
| 0 | 0 | $100 | $100 | - | - | - |
| 100 | $100 | $100 | $200 | 100 / 100 | 100 / 100 | $200/100=$2.00 per unit |
| 230 | $200 | $100 | $300 | $0.87 | $0.43 | $300/230=$1.30 per unit |
| 290 | $300 | $100 | $400 | $1.03 | $0.34 | $400/290=$1.38 per unit |
| 350 | $400 | $100 | $500 | $1.14 | $0.29 | $500/350=$1.43 per unit |
| 380 | $500 | $100 | $600 | $1.32 | $0.26 | $600 / 380=$1.58 per unit |
| 400 | $600 | $100 | $700 | $1.50 | $0.25 | $700/400=$1.75 per unit |
| 390 | $700 | $100 | $800 | $1.79 | $0.26 | $800/390=$2.05 per unit |
Now that we now know how to calculate the various averages, or per unit costs, let’s plot these three averages against the levels of output, so that we can visualize the shape of the lines. In the graph below notice that the AFC (blue) curve is diving toward the horizontal axis. Do you think that if C&C Family Farm increases the level of output to 100 million pounds that the fixed cost of $100 will actually become zero? In truth, the AFC will always be some tiny but positive cost value.
EXAMPLE
Are you wondering what “tiny but positive cost value” means? Suppose you produce a product at the cost of $100 per unit. If you make 100 units, then AFC is $0.10 (1/100). If you produced 1,000,000, then AFC is $0.000001 (1/1,000,000)—a tiny but positive cost value.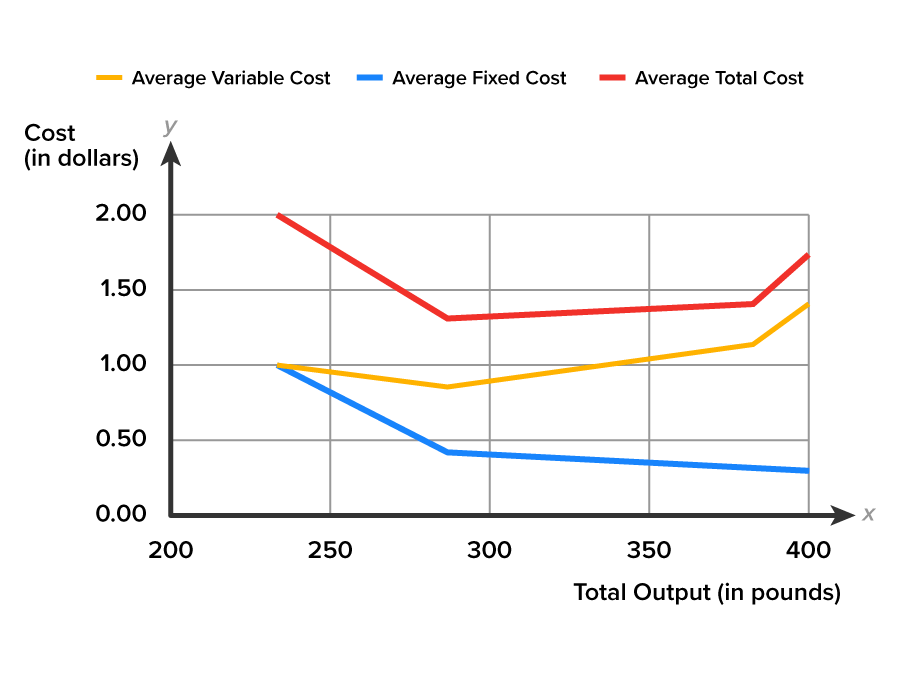
The AVC (yellow) curve in the graph above has a general “U” shape. In the data table above, it is noted that C&C Family Farm’s average variable cost began at $1 per unit. The AVC decreases, before starting to increase. The “U” shape of the AVC curve confirms this trend.
The ATC (red) curve is higher than either the AFC or AVC, as we would expect. Why? Because ATC is the sum of AFC and AVC. This is a second way to calculate ATC.
Does the shape of the ATC curve look like the shape of the AVC curve? It should. The difference between the ATC and AVC curves is the AFC curve. So if you pick any level of output on the horizontal axis, say 350 units, and estimate the cost difference between ATC and AVC, you should get the value for AFC at that level of production.
To explore this concept, consider the following example. At the output level of 350 units, the ATC is $14.3 per unit, AVC is $1.14 per unit, and AFC is $0.29 per unit. If we subtract AVC from ATC, we will get the AFC. $1.43 (ATC) - $1.14 (AVC) = $0.29 (AFC). The distance between the ATC and AVC curves in the graph is equal to $0.29, where the AFC at 350 units of output. Look back to the costs of production table for 350 units of total output. Can you confirm that our calculation is correct?
Notice that the ATC curve has a “U” shape similar to the AVC. The ATC curve starts off relatively high, because at low levels of output total costs are dominated by the fixed cost. Mathematically, the denominator (units of output) is so small in the beginning of production that the average total cost is large. ATC then declines, as the fixed costs are spread over an increasing quantity of output. But as output expands still further, the ATC begins to rise, as AVC increases with larger quantities of production. The right side of the ATC curve will begin rising more rapidly, as the production process experiences diminishing marginal productivity. The additional output per additional worker diminishes. Production and costs have an inverse relationship.
We now know how to calculate average, or per unit costs. And we’ve become acquainted with the shape of the ATC, AFC, and AVC curves.
Suppose you are the owner of a business, what could you possibly do with this information? Might you use average cost information as one method for pricing your products? The average measures cost on a per unit (rather than a total) basis. It could prove useful!
EXAMPLE
Duangjan was worried that the cost of production was higher than expected for her Japanese street fashion inspired clothing and accessories for children. Can Duangjan use the cost information to help set the price of the clothing items to make sure her business is successful? Yes, Duangjan can use the cost information to calculate the average cost per unit of her items. Average cost information is easy to calculate for a business, and can help Duangjan understand how to price her clothing items.Source: THIS TUTORIAL HAS BEEN ADAPTED FROM LUMEN LEARNING’S “Microeconomics”. ACCESS FOR FREE AT https://courses.lumenlearning.com/wm-microeconomics/. LICENSE: CC ATTRIBUTION 4.0 INTERNATIONAL.