Converting Units

1. Introduction to Converting Units

Unit conversion is a simple process to overlook, but doing so can have dramatic effects on the results of any project we may be working on. For example, suppose someone told us that a machine needs to be able to handle a 50,000 N load. If we were in a country that uses the metric system, that may make perfect sense to us. If we are in the United States, where English units are used, that may not make any sense at all. The need then arises to convert 50,000 N into pounds (lbs), so that we can more easily understand the quantities we are working with. Unit conversion allows us to express 50,000 N as roughly 11,240 lbs, or 5.62 tons. While the numbers and units are different, the actual quantity they represent is the same.

big idea

Notice that each of these values has different units, but they represent the same amount of force. That is why unit conversion is important. It allows us to represent quantities in terms of measurements we understand or need to work with.

learn more

Knowing how to convert between the two systems allows for better comprehension of instructions, weights, recipes, and distances, among other everyday information.

Today, conversion calculators are widely available on the internet and as mobile apps and will perform conversions between units quicky and easily. This Conversion Calculator www.calculator.net/conversion-calculator.html is one such resource.

To further understand how to perform these conversions yourself, check out this conversion resource conversion resource.

Let’s next look at how to do some unit conversion.

2. Simple Unit Conversion

To convert units, we first need to understand something called a conversion factor, which is basically a fraction equal to 1 that relates two different units.

step by step

1. List the value you are given.
2. Determine the conversion factor.
3. Multiply the conversion factor by the given value, making sure that the units we start with cancel, and the unit we are looking for will be left.
4. Simplify as needed.

EXAMPLE

Suppose we have 160 cups of water, and we want to determine how many gallons of water this is. Before we make any calculations, we might recall that there are 16 cups in one gallon of water. This knowledge will help us determine what our conversion factor will be.

So, how do we begin converting?

For the problem involving cups to water, here is what this would look like:

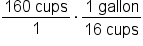
	Conversion factor: 1 gallon = 16 cups Place 16 cups in the denominator so that the “cups” cancel.
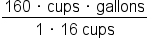
	Multiply across numerators and denominators.
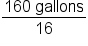
	The units of cups cancel.
	Our solution

try it

Try doing the following calculations on your own and then check the solutions.

Convert 7200 seconds into hours, using the fact that 1 hour = 3600 seconds.

	Conversion factor: 1 hour = 3600 seconds
	Multiply across numerators and denominators.
	The units of seconds cancel.
	Our solution

Convert 2 miles into feet, using the fact that 1 mile = 5280 feet.

	Conversion factor: 5280 feet = 1 mile
	Multiply the numerators and denominators.
	Our solution

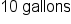
3. Multi-Step Unit Conversion

In the above example of converting seconds to hours, suppose we did not know a conversion factor between hours and seconds. Do you think we can make the conversion?

Of course! In cases such as this, we may wish to use multiple conversion factors to help us make a conversion. For example, we may know that there are 60 seconds in 1 minute, and 60 minutes in 1 hour.

Therefore, we can do the following:

EXAMPLE

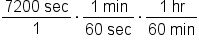
	Conversion factors: 1 min = 60 sec; 1 hr = 60 min
	Multiply the numerators and denominators.
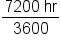
	The units of seconds and minutes cancel, leaving hours.
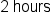
	Our solution

try it

Try your hand at converting 3 meters into inches. Note that there are 2.54 centimeters in 1 inch, and 100 centimeters in 1 meter.

Convert 3 meters into inches.

To solve this problem, we can implement the conversion factors 2.54 centimeter = 1 inch and 100 centimeter = 1 meter, and string the conversion factors together.

	Conversion factors: 1 m = 100 cm; 1 in = 2.54 cm
	Multiply the numerators and denominators.
	The units of meters and centimeters cancel, leaving inches.
	Our solution