In this lesson, you will deepen your understanding of decimals and fractions by converting between the two. You will also examine how these conversions strengthen your results driven skill. Specifically, this lesson will cover:
1. Converting a Fraction Into a Decimal
As you’ve seen so far, many of the numbers used in mathematics can be written as both a fraction and a decimal. If you remember, these numbers are called rational numbers. Rational numbers have a fraction and a decimal form, which are equivalent. Converting between decimals and fractions is very useful when working with measurements, as well as everyday situations such as percentages. These conversions can help you meet goals such as finding correct measurements on home renovations or evenly dividing food between several people.
-
EXAMPLE
If you look at this ruler, which is measuring in centimeters, you can see 3.5 centimeters marked on it. You can also think of 3.5 centimeters as a fraction. The tick mark is halfway between the 3 and the 4, which is 3 ½ centimeters.
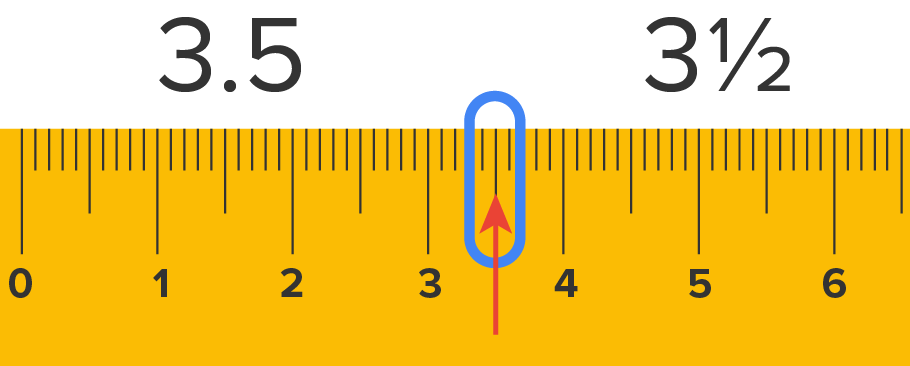
So, ½ or 0.5 may be one that you already know. For example, 50 cents is ½ of a dollar. But how do you do this mathematically with less familiar numbers? Division! You divide the denominator into the numerator.
-
EXAMPLE
Write
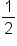
as a decimal.
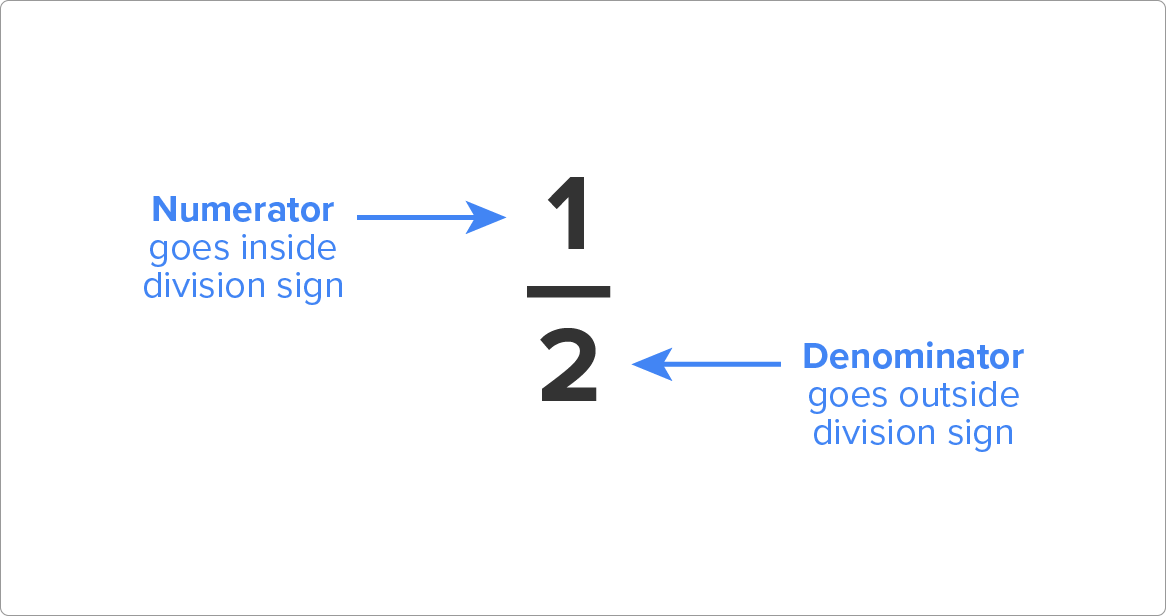
- Place the numerator, 1, inside the division sign and the denominator, 2, outside the division sign.
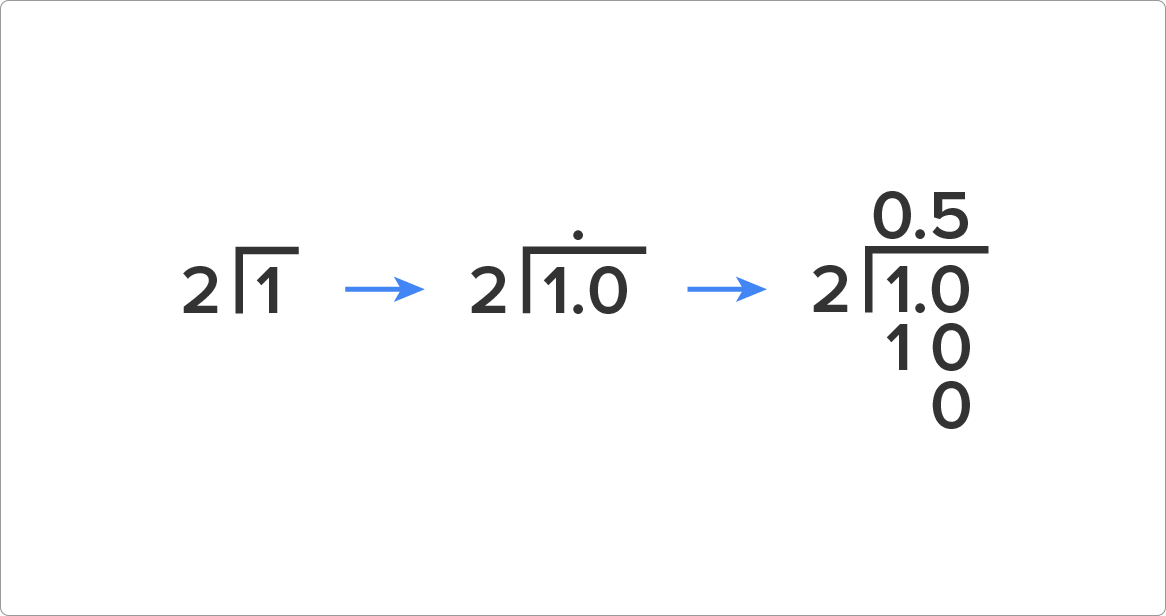
- Because 2 cannot divide into 1, add a decimal point and a zero. Remember, $1 is the same as $1.00. Move the decimal point directly above (like we covered when dividing decimals).
- Divide 2 into 10. Two divides evenly into 10, 5 times. We place a 5 over the 10. With the placement of the decimal, we get 0.5.
- Because there is no remainder, you are done. ½ is equal to 0.5.
-
EXAMPLE
Write
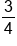
as a decimal.

- Place the numerator, 3, inside the division sign and the denominator, 4, outside the division sign.
- You cannot divide 4 into 3, so add a decimal and a zero. Then move the decimal up into your answer.
- You can now divide 4 into 30, 7 times with a remainder of 2. Because we’ve committed to a decimal, we cannot have a remainder so add another zero and bring it down to make it 20.
- Divide 4 into 20 to get 5. You have no remainder so you are done.
-
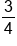 is equal to 0.75.
is equal to 0.75.
-
EXAMPLE
Write
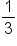
as a decimal.
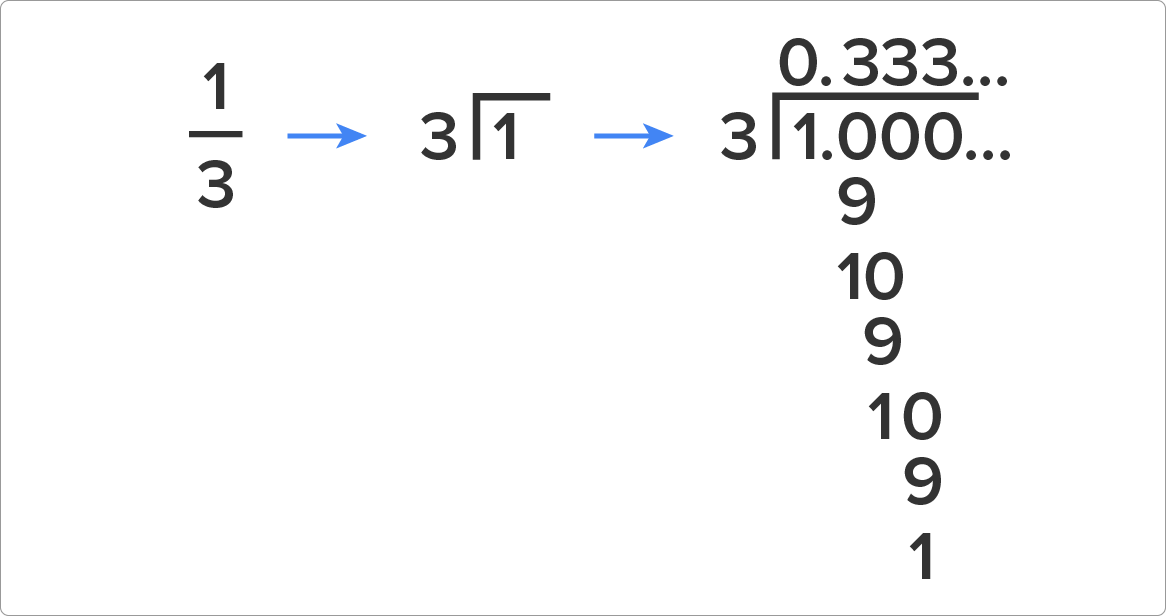
- Divide the denominator into the numerator.
- You cannot divide 3 into 1, so add a decimal and a zero. Then move the decimal up into your answer before you forget.
- You can now divide 3 into 10, 3 times with a remainder of 1. Again, you cannot have a remainder so add another zero and bring it down.
- Divide 3 into 10 to get 3 with a remainder of 1. Again, you cannot have a remainder, so add another zero and bring it down.
- Stop—are you noticing something about your answer? The 3 keeps repeating and will always repeat. When you have a repeating decimal, you can stop and add a line over the top called a “bar” to show everyone that that value repeats forever.
- Our solution is
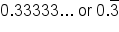 .
.
-
Consider the fraction
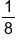
.
How would you write this fraction as a decimal?
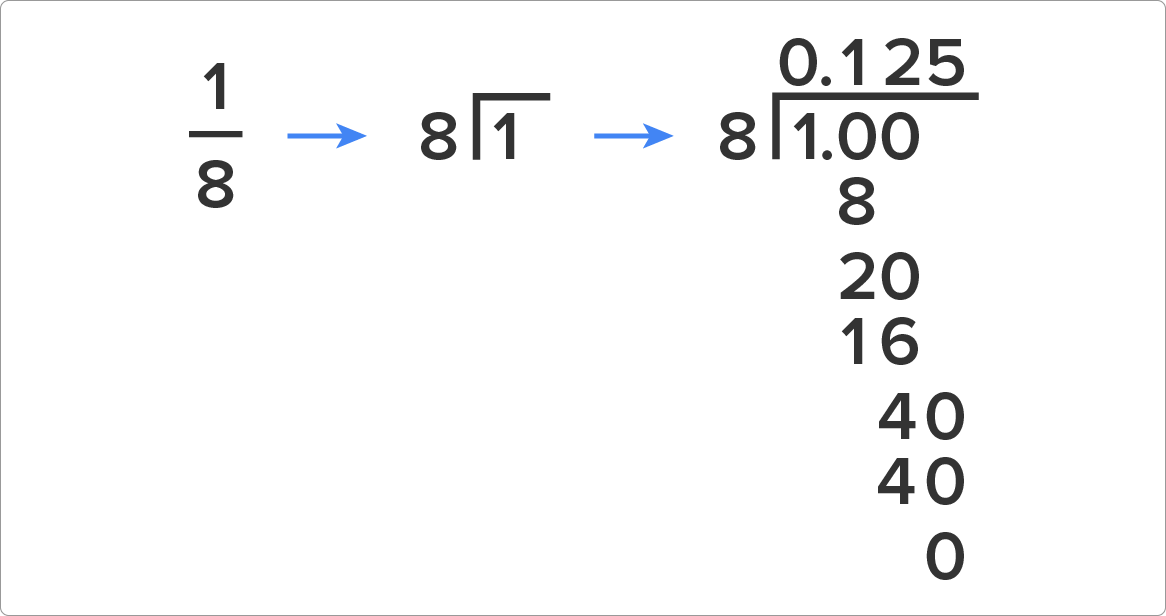
- Divide the denominator into the numerator.
- You cannot divide 8 into 1, so add a decimal and a zero. Then move the decimal up into your answer before you forget.
- You can now divide 8 into 10, 1 time with a remainder of 2. Again, you cannot have a remainder so add another zero and bring it down.
- Divide 8 into 20 to get 2 with a remainder of 4. Again, you cannot have a remainder, so add another zero and bring it down.
- Divide 8 into 40 to get 5. You have no remainder now so you are done.
- Our solution is 0.125.
2. Converting a Mixed Number into a Decimal
So far, we have only converted a fraction into a decimal, but what if you have a mixed fraction (a fraction and a whole number)? There are two ways you can convert these into a decimal.
-
EXAMPLE
Write
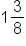
as a decimal
Method #1: Convert to an Improper Fraction
Convert the mixed fraction into an improper fraction to get rid of the whole number. Remember, we do this by multiplying the denominator (8) times the whole number (1), and then adding the numerator (3). This will give us 11/8. Now you can divide as we have earlier.
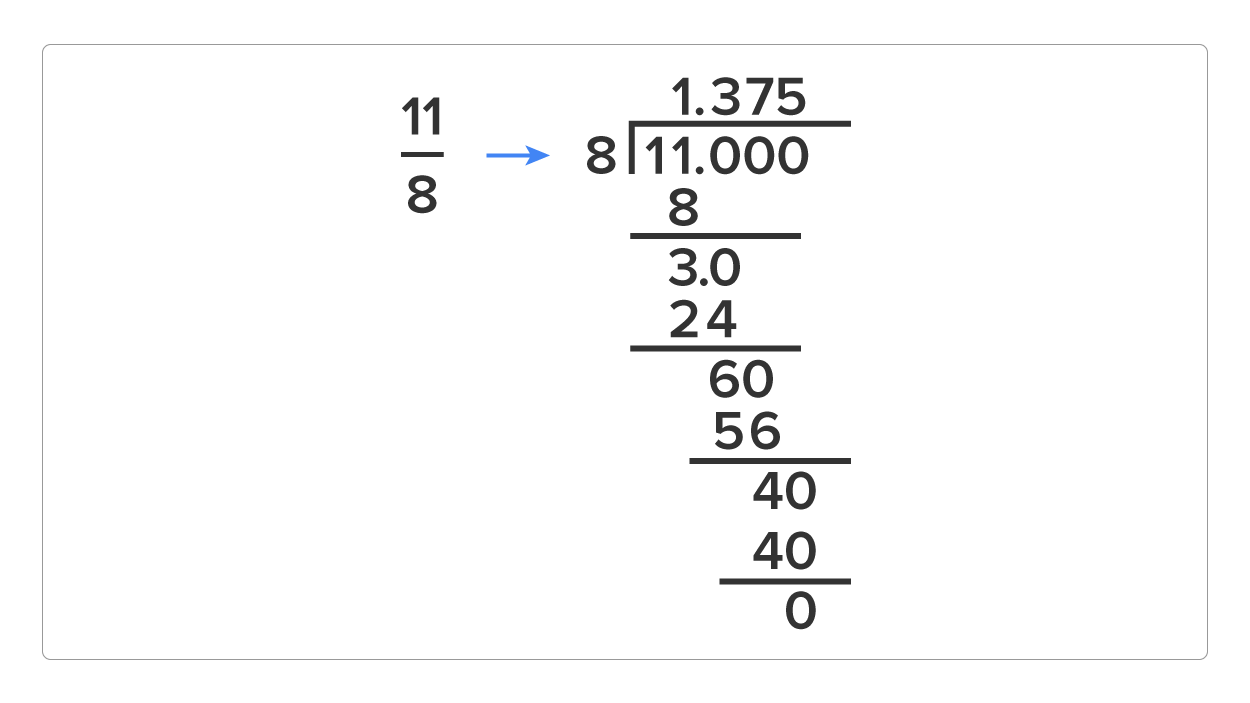
- Divide the denominator into the numerator.
- Move the decimal point up into your answer before you forget and then start dividing.
- Divide 8 into 11, 1 time with a remainder of 3. Because you cannot have a remainder, add a zero after your decimal point and bring it down.
- Now you can divide 8 into 30, 3 times with a remainder of 6. Again, you cannot have a remainder so add a zero and divide 8 into 60, 7 times with a remainder of 4.
- Add another zero and divide 8 into 40, 5 times. There is no remainder, so you’re done.
- Our solution is 1.375.
Method #2: Converting the Fraction Only
Ignore the whole number for now and just convert the fraction.
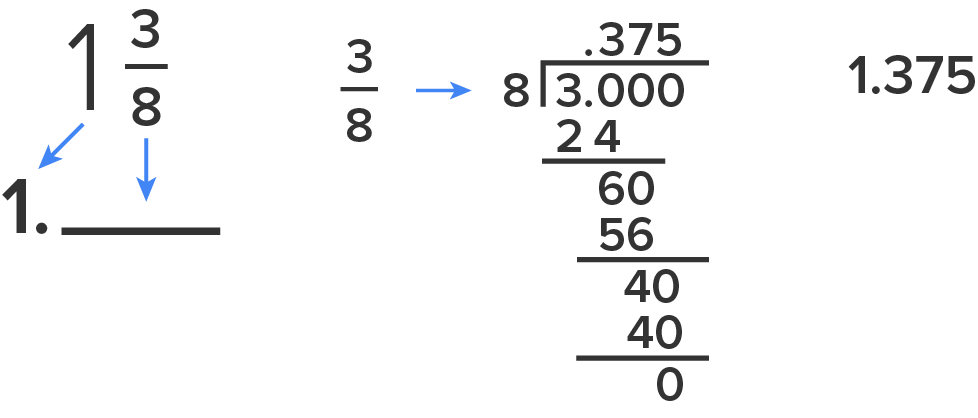
- Divide the denominator into the numerator.
- You cannot divide 8 into 3 so add a decimal point and a zero. Move the decimal point up into your answer before you forget.
- Divide 8 into 30, 3 times with a remainder of 6. Again, you cannot have a remainder so add a zero and bring it down.
- Divide 8 into 60, 7 times with a remainder of 4.
- Add another zero and divide 8 into 40, 5 times. There is no remainder, so you’re done with the fraction conversion.
- Add the whole number back in to get your solution.
- Our solution is 1.375.
-
Consider
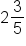
.
Write this fraction as a decimal.
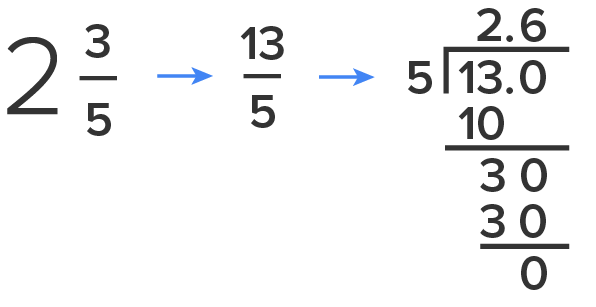 Method #1: Convert to an Improper Fraction
Method #1: Convert to an Improper Fraction
- Convert the mixed number into an improper fraction by multiplying the denominator with the whole number and then adding the numerator.
- Divide 13 by 5. 5 can go into 13 twice, but there is a remainder so add a decimal and a zero. 5 can go into 3, 6 times. There is no remainder at this point so you are done.
- Our solution is 2.6.
Method #2: Converting the Fraction Only
- Divide the denominator into the numerator.
- You cannot divide 5 into 3 so add a decimal and a zero. Move the decimal up into your answer.
- Now you can divide 5 into 30 to get 6. There is no remainder so you are done.
- Our solution is 0.6.
- Add the 2 back into the decimal for 2.6.
3. Converting a Decimal Into a Fraction
Now that you know how to convert a fraction to a decimal by dividing, how do you convert a decimal back into a fraction? To convert a decimal to a fraction, you can use the concept of decimal place value. Place value refers to where a number is located in relation to the decimal point. In the diagram below, the number 0.1234 shows the 1 in the tenths place, the 2 in the hundredths place, the 3 in the thousandths place, and the 4 in the ten-thousandths place.
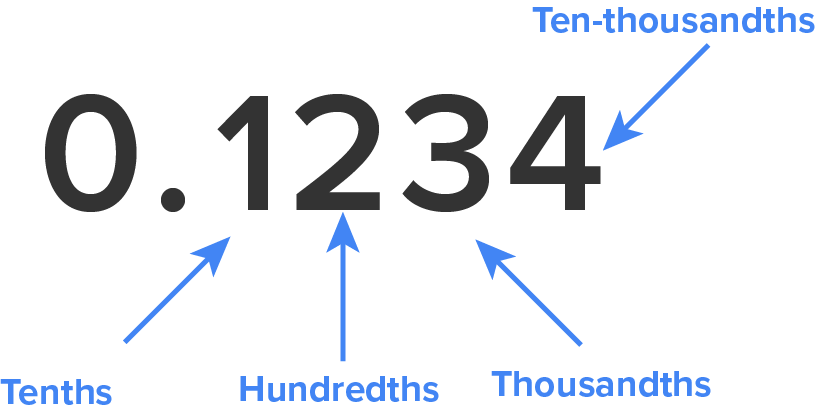
The fraction equivalent of a decimal is determined by the digits and their decimal place value.
-
Do you struggle with knowing which place the last decimal is in is called? When converting decimals to fractions using decimal place value, your denominators are always a power of 10, which is a 1 followed by a number of zeros. Just count the amount of numbers after the decimal place; that is the amount of zeros in your denominator.
|
Decimal
|
Fraction
|
Explanation
|
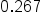
|
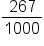
|
0.267 is equivalent to the fraction 267/1000, because the last digit, 7, is in the thousandths place. So, we would place a 1000 in the denominator. Using our hint, we also know that 0.267 has 3 digits after the decimal place, so the number in the denominator is a 1 followed by 3 zeros (1000).
|
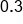
|
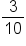
|
In the decimal 0.3, 3 is in the tenths spot, so the fraction equivalent is 3/10. There is 1 digit after the decimal 0.3, so the denominator is 1 followed by 1 zero (10).
|
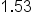
|
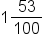
|
1.53 has 3 in the hundredths spot, so the fraction equivalent is 53/100. But, note that there is a whole number in front of the decimal. We would convert the decimal portion of the number (.53) to a fraction, and then place the whole number (1) in front of the fraction to make a mixed fraction.
|
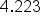
|
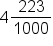
|
For 4.223, the 3 following the decimal is in the thousandths place, so the fraction equivalent is 223/1000. We then place the whole number (4) in front of the fraction.
|
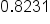
|
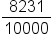
|
In the final example, for the decimal 0.8231, the 1 is in the ten-thousandths place, so the fraction equivalent is 8231/10000. Note that there are 4 digits after the decimal in 0.8231, so there will be 4 zeros in the denominator.
|
-
EXAMPLE
Suppose you want to convert the decimal 0.34 into a fraction. To determine the denominator of your fraction, look at the nonzero digit of the decimal that is farthest to the right. In this case, the 4 is in the hundredths place. Therefore, 0.34 as a fraction is 34/100.
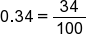
Unlike the fractions we’ve done so far in this lesson, this fraction can be simplified. Remember, you can simplify the fraction by finding the greatest common factor of the numerator and the denominator. The factors of 34 are 1, 2, 17, and 34. The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100. The common factors are 1 and 2, so the greatest, or largest, common factor is 2. The shared factors can be canceled out by dividing both the numerator and denominator by the greatest common factor. Therefore, when you simplify 34/100, you divide 34 by 2 and 100 by 2:
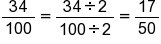
-
Any common factor can be used to reduce a fraction, but further simplification will be necessary. However, using the greatest common factor will always produce a fraction in simplest form. You will know that your fraction is in its simplest form because the greatest common factor of the numerator and denominator is 1.
-
Suppose you have the decimal 1.205.
Convert this decimal to a fraction and simplify.The last digit, 5, is in the thousandths spot, so the fraction equivalent is 205/1000. We then add the whole number in front of the fraction to create a mixed number, 1 205/1000. The greatest common factor of 205 and 1000 is 5. Therefore, you can simplify the fraction portion by dividing both the numerator and denominator by 5. Therefore, 1 205/1000 becomes 1 41/200.
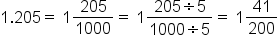
-
-
What if you had been trying to convert the decimal
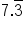
to a fraction? That would have been challenging to determine the fraction, so let’s make this easy. Below are the most common fractions and decimal equivalents. They are worth remembering since they will save you a lot of time in the future.
So in the example above,
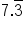
could be written as
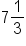
.
Imagine that you have created a budget and you want to put 1/10 of your earnings into a savings account. On your paycheck, you receive $528.50. In order to determine how much of this paycheck you save, it’s easiest to convert one-tenth into a decimal because the amount of the paycheck is provided as decimal, rather than a fraction. By using the steps in this unit, you find that 1/10 is 0.10. You can then multiply 0.10 by 528.50 and determine that you should put $52.85 into your savings account.
Today we reviewed decimal and fraction real numbers. We then learned how to convert a fraction to a decimal by dividing the denominator into the numerator. Converting mixed numbers to a decimal is a special case and can be solved using two different methods. Decimals can also be converted into fractions by determining the digits and their decimal place value and placing that value over the appropriate denominator. By converting fractions and decimals, you are strengthening your ability to get results efficiently and meet your goals.
Best of luck in your learning!

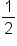 as a decimal.
as a decimal.


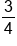 as a decimal.
as a decimal.

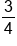 is equal to 0.75.
is equal to 0.75.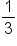 as a decimal.
as a decimal.

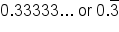 .
.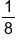 .
.
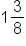 as a decimal
as a decimal

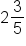 .
.

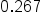
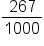
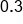
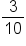
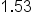
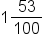
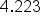
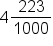
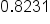
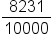
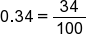
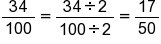
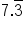 to a fraction? That would have been challenging to determine the fraction, so let’s make this easy. Below are the most common fractions and decimal equivalents. They are worth remembering since they will save you a lot of time in the future.
to a fraction? That would have been challenging to determine the fraction, so let’s make this easy. Below are the most common fractions and decimal equivalents. They are worth remembering since they will save you a lot of time in the future.
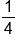
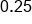
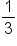
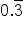
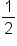
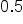
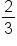
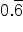
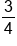
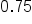
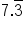 could be written as
could be written as 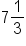 .
.