Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Converting Between Forms of Linear Equations

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to convert a linear equation from standard or point-slope form to slope-intercept form. Specifically, this lesson will cover:

Table of Contents

1. Review of Slope-Intercept Form

Linear equations can be written in several forms: (a) Slope-Intercept Form, (b) Point-Slope Form and (c) Standard Form. Each form has its pros and cons as to why we would want to express the equation in such a format. This is because certain information about the line and the linear relationship it represents can be easily identified just by looking at its equation. We have reviewed the first form, slope-intercept form.

The equation of a line written in slope-intercept form is: 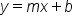y equals m x plus b.

We refer to this form as slope-intercept form because the equation readily gives us information about the line's slope and its y-intercept. The variable m represents slope, and the variable b represents the y-coordinate of the y-intercept. The variable b in the equation represents the y-intercept of the line. The coordinate point of the y-intercept is 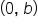left parenthesis 0 comma space b right parenthesis and the y-intercept is the location on a graph where a line or a curve intersects the y-axis.

2. Point-Slope Form

Linear equations can also come written in point-slope form. Point-slope form, as the name suggests, provides information about the line's slope, and a point on the line. The equation has the y variable on one side of the equation and the slope, m, and x variable on the other side of the equation.

formula to know
Point-Slope Form of a Line
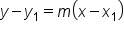
y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses

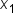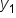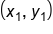Once again, we can easily identify the line's slope by the variable m. We also have x subscript 1 and y subscript 1 or open parentheses x subscript 1 comma space y subscript 1 close parentheses. These represent the x-coordinate and y-coordinate of a point on a line. Here is an example of an equation written in point-slope form:

EXAMPLE

Identify the slope and a point from the point-slope equation: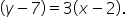 open parentheses y minus 7 close parentheses equals 3 open parentheses x minus 2 close parentheses.

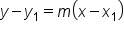
y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses Point-slope form of a line
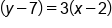
open parentheses y minus 7 close parentheses equals 3 open parentheses x minus 2 close parentheses The equation
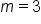
m equals 3 The line has a slope of 3.
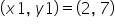
left parenthesis x 1 comma space y 1 right parenthesis equals left parenthesis 2 comma space 7 right parenthesis A given point on the line is (2, 7).

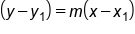Notice the equation open parentheses y minus y subscript 1 close parentheses equals m open parentheses x minus x subscript 1 close parentheses again. There is a 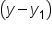open parentheses y minus y subscript 1 close parentheses, or minus sign in front of 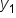y subscript 1. 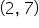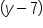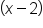So, plugging the point left parenthesis 2 comma space 7 right parenthesis into the equation becomes left parenthesis y minus 7 right parenthesis and left parenthesis x minus 2 right parenthesis.

EXAMPLE

A line has a slope of 2 and passes through the point (4, -3). Write the equation in point-slope form.

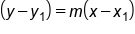
open parentheses y minus y subscript 1 close parentheses equals m open parentheses x minus x subscript 1 close parentheses Point-slope form
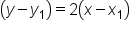
open parentheses y minus y subscript 1 close parentheses equals 2 open parentheses x minus x subscript 1 close parentheses Plug in the slope of the equation as m.
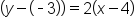
open parentheses y minus open parentheses short dash 3 close parentheses close parentheses equals 2 open parentheses x minus 4 close parentheses Plug in the point (4, -3).
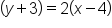
open parentheses y plus 3 close parentheses equals 2 open parentheses x minus 4 close parentheses Keep track of the negative signs within the equation. Notice the y-value of -3 becomes a +3 within the equation.

3. Standard Form

The final form we will discuss in this lesson is called standard form. Unlike slope-intercept form, or point-slope form, we cannot readily identify the slope, y-intercept, or point on a line simply by looking at the equation in standard form. However, the benefit of standard form is that any linear equation can be written in standard form, whereas not every line can be written in slope-intercept or point-slope forms. Think about a vertical line. It has an undefined slope. Both slope-intercept and point-slope forms rely on a defined slope to generate their respective equations. A vertical line, however, can be written in standard form, because a slope is not needed to write its equation.

formula to know
Standard Form of a Line
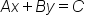
A x plus B y equals C

Notice that in standard form, the x and y variables are on the same side of the equation. In slope-intercept and point-slope forms, the y and x variables are on opposite sides of the equations.

A couple of notes about generally accepted rules for equations written in standard form:

  • A, B, and C should be integers. If any of them are not, the entire equation should be multiplied so that they are, if possible.
  • The integer A should be a positive integer. B and C are allowed to be negative, but if A is negative, the equation should be multiplied by -1 so as to make A positive.
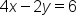  • Wherever possible, A, B, and C should be relatively prime. This means that they should have no common factors other than 1, if possible. For example, mathematicians prefer 4 x minus 2 y equals 6 to be written as 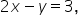2 x minus y equals 3 comma canceling out the common factor of 2 in Ax, By and C.

4. Why and When to Convert

Now we are familiar with the three forms of linear equations. Sometimes it is beneficial to have the equation of a line written in a different form, so that you can more readily ascertain certain information about the line just by looking at its equation. For example, having an equation written in standard form doesn't make it easy to identify the line's slope, or at least not as easy as the same line written in slope-intercept form or point-slope form. Likewise, if an equation is written in point-slope form, and you wish to easily identify the line's y-intercept, converting the equation into slope-intercept form will be helpful.

5. Convert from Standard Form to Slope-Intercept Form

Let’s start with converting from standard form to slope-intercept form. Again, in standard form, the x and y variables are on the same side of the equation. To convert to slope-intercept form, the equation should be solved in terms of y and simplified.

EXAMPLE

Consider the equation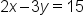 2 x – 3 y equals 15. Write the equation in slope-intercept form.

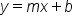If we wish to identify the line's slope and intercept, it would be wise for us to convert this equation into slope-intercept form, y equals m x plus b, so we can simply look at m and b for that information. As you read the steps below, keep in mind that the overall goal is to get the y variable by itself on one side of the equation, and then cancel the coefficient in front of y.

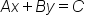
A x plus B y equals C Standard form of a line
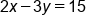
2 x minus 3 y equals 15 The equation.
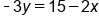
short dash 3 y equals 15 minus 2 x Subtract 2x from both sides.
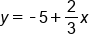
y equals short dash 5 plus 2 over 3 x Divide all parts by -3 (note the x-term coefficient is now positive).
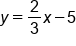
y equals 2 over 3 x minus 5 Rearrange to be in slope-intercept form y equals m x plus b.

Now it is clear that the line has a slope of two-thirds and a y-intercept at (0, -5).

big idea
When converting from standard form to slope-intercept form, isolate the y-term to one side of the equation, and then divide by its coefficient. This will leave y alone on one side of the equation. Then, just rearrange the terms so that mx is first, and b follows.

6. Convert from Point-Slope Form to Slope-Intercept Form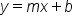

Both point-slope form and slope-intercept form provide information about a line's slope. Point-slope form can give the location to any point on the line, whereas slope-intercept form gives only the y-coordinate to the y-intercept.

EXAMPLE

You may be given that a line has a slope of 4 and passes through the point (-3, 7). How can you draw information about the line's y-intercept?

We'll need to convert from point-slope form to slope-intercept form.

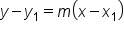
y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses Point-slope form of a line
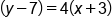
open parentheses y minus 7 close parentheses equals 4 open parentheses x plus 3 close parentheses Substitute the information we know: slope of 4 and passes through (-3, 7). Note the +3 in the equation corresponds to the -3 value of the point.
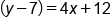
open parentheses y minus 7 close parentheses equals 4 x plus 12 Distribute 4 into (x + 3).
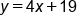
y equals 4 x plus 19 Add 7 to both sides.
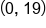
left parenthesis 0 comma space 19 right parenthesis This is the y-intercept.

big idea
To convert from point-slope form into slope-intercept form, distribute the slope, m, into the expression in parentheses. Then move the constant term attached to y to the other side of the equation. Finally, combine like terms to arrive at the equation in slope-intercept form.

summary
In this lesson, you began with a review of slope-intercept form and learned that in addition to slope-intercept form, linear equations can also be written in point-slope form and standard form. Each form has its pros and cons as to their use, because certain information about the line and the linear relationship it represents can be easily identified simply by looking at its equation. Point-slope form, for example, provides information about the line's slope, and a point on the line. In standard form equations, you cannot readily identify the slope, y-intercept, or point on a line simply by looking at the equation; however, any linear equation can be written in standard form. When understanding why and when to convert between forms, you learned that it is beneficial to have the equation to the same line written in different forms so that you can more readily draw certain information about the line just by looking at its equation. Lastly, you learned how to convert from standard form to slope-intercept form and convert from point-slope form to slope-intercept form.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Formulas to Know
Point-Slope Form of a Line

y minus y subscript 1 equals m open parentheses x minus x subscript 1 close parentheses

Standard Form of a Line

A x plus B y equals C

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.