Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Converting a Quadratic Equation into Vertex Form

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn how to write a quadratic equation in vertex form. Specifically, this lesson will cover:

Table of Contents

1. Vertex Form of a Quadratic Equation

Quadratic equations written in vertex form provide readily available information about the the parabola it represents on a graph. The variables h and k form a coordinate pair (h, k) and represent the vertex of the parabola.

formula to know
Vertex Form of a Quadratic Equation
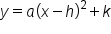
y equals a left parenthesis x minus h right parenthesis squared plus k

The vertex is the maximum or minimum point to the parabola (depending on if the graph opens upward or downward). Using the vertex form of quadratic equations can be ideal for graphing parabolas because we can easily identify the vertex, plot points on one side of the vertex, and then reflect them across the axis of symmetry on which the vertex lies.

2. Comparing Standard Form to Vertex Form

Recall that the standard form of quadratic equations expresses the quadratic in expanded terms, containing an x-squared term, an x-term, and a constant term.

formula to know
Standard Form of a Quadratic Equation
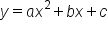
y equals a x squared plus b x plus c

On the other hand, equations in vertex form resemble the factored form of a quadratic, with a linear binomial 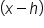open parentheses x minus h close parentheses raised to the second power.

We can use a process called completing the square to write an expanded quadratic as a factor squared. In order to do this, our expanded quadratic must be a perfect square trinomial. In other words, half of the x-term coefficient squared is equal to the constant term.

EXAMPLE

Rewrite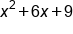 x squared plus 6 x plus 9 as a factor squared.

x squared plus 6 x plus 9 Half of 6 is 3. 3 squared is 9. This is a perfect square trinomial.
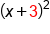
open parentheses x plus 3 close parentheses squared Perfect square trinomials can be written as a binomial squared.

hint
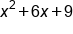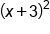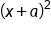We were able to rewrite x squared plus 6 x plus 9 as open parentheses x plus 3 close parentheses squared because we recognized that if we halved the x-term coefficient, and then squared it, the result would be the constant term. Half of the x-term coefficient then becomes the value that accompanies x in the binomial squared open parentheses x plus a close parentheses squared.

3. Converting a Quadratic from Standard Form into Vertex Form

In order to rewrite a quadratic equation from standard form to vertex form, we need be able to recognize the perfect square trinomial relationship. Often times, this isn't readily provided to us, and we need to do some algebraic manipulation, with a process known as completing the square. You may have had some practice completing the square when learning about solving or factoring quadratic equations. To complete the square within this context, we perform the following steps:

step by step
  1. Move the constant term to the other side of the equation.
  2. Factor out the x-squared coefficient on one side of the equation.
  3. Separately, divide the x-term coefficient and square it.
  4. Add this quantity to both sides of the equation.
  5. Recognize part of the expression as a perfect square trinomial and express it as a binomial squared.
  6. Isolate y by moving other terms to the other side of the equation.
  7. Simplify the expression, leading to the equation in vertex form.

There are quite a few steps involved in this process, so we are going to take a look at an example step-by step.

EXAMPLE

Rewrite the equation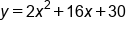 y equals 2 x squared plus 16 x plus 30 in vertex form.

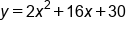
y equals 2 x squared plus 16 x plus 30 Move the constant term to the other side of the equation
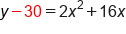
y minus 30 equals 2 x squared plus 16 x Factor out the x-squared coefficient
y minus 30 equals 2 open parentheses x squared plus 8 x close parentheses Separately, divide the x-term coefficient by 2, and square it.
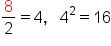
8 over 2 equals 4 comma space space space 4 squared equals 16 Add the quantity from the previous step to both sides of the equation. Don't forget to add the full value to the left side!
y minus 30 plus 32 equals 2 open parentheses x squared plus 8 x plus 16 close parentheses Recognize part of the expression as a perfect square trinomial and express it as a binomial squared
y plus 2 equals 2 open parentheses x plus 4 close parentheses squared Isolate y by moving other terms to the other side of the equation
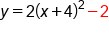
y equals 2 open parentheses x plus 4 close parentheses squared minus 2 Our solution

Notice how we added 16 in the 4th step. This quantity was found by dividing 8 by 2 and then squaring it. We added it within the parentheses, with a factor of 2 outside. Due to this outside factor of 2, we actually added 32 to that side of the equation, not 16. This is why we see + 32 on the left side of the equation. When performing this step, it is important to multiply this quantity by the outside factor when adding a quantity on the other side to keep the equation balanced.

Now we have an equation equivalent to the equation given to us in standard form. If we were to graph the two equations, we would get the same parabola. However, you may prefer to work with the equation in vertex form, as this form gives the coordinates of the vertex (h, k).

summary
The vertex of a parabola can be readily identified in the vertex form of a quadratic equation, because h and k form the x and y-coordinates of the vertex. The vertex of a parabola is the minimum point--in the case of an upward facing parabola--or the maximum point--in the case of a downward facing parabola, and also lies on the parabola's axis of symmetry. When comparing standard form to vertex form, standard form is the expanded form while the vertex resembles a factored form. Completing the square is used to write a quadratic expression in expanded form into a binomial squared. This is useful when converting an equation in standard form into vertex form.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License

Formulas to Know
Standard Form of a Quadratic Equation

y equals a x squared plus b x plus c

Vertex Form of a Quadratic Equation

y equals a left parenthesis x minus h right parenthesis squared plus k

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.