Table of Contents |
A function is called continuous at a point where there is no break in the graph at that point.
That is, 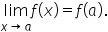
Consider the graph of  shown below. We will examine the continuity of
shown below. We will examine the continuity of  when x = 1, 2, 3, and 4.
when x = 1, 2, 3, and 4.
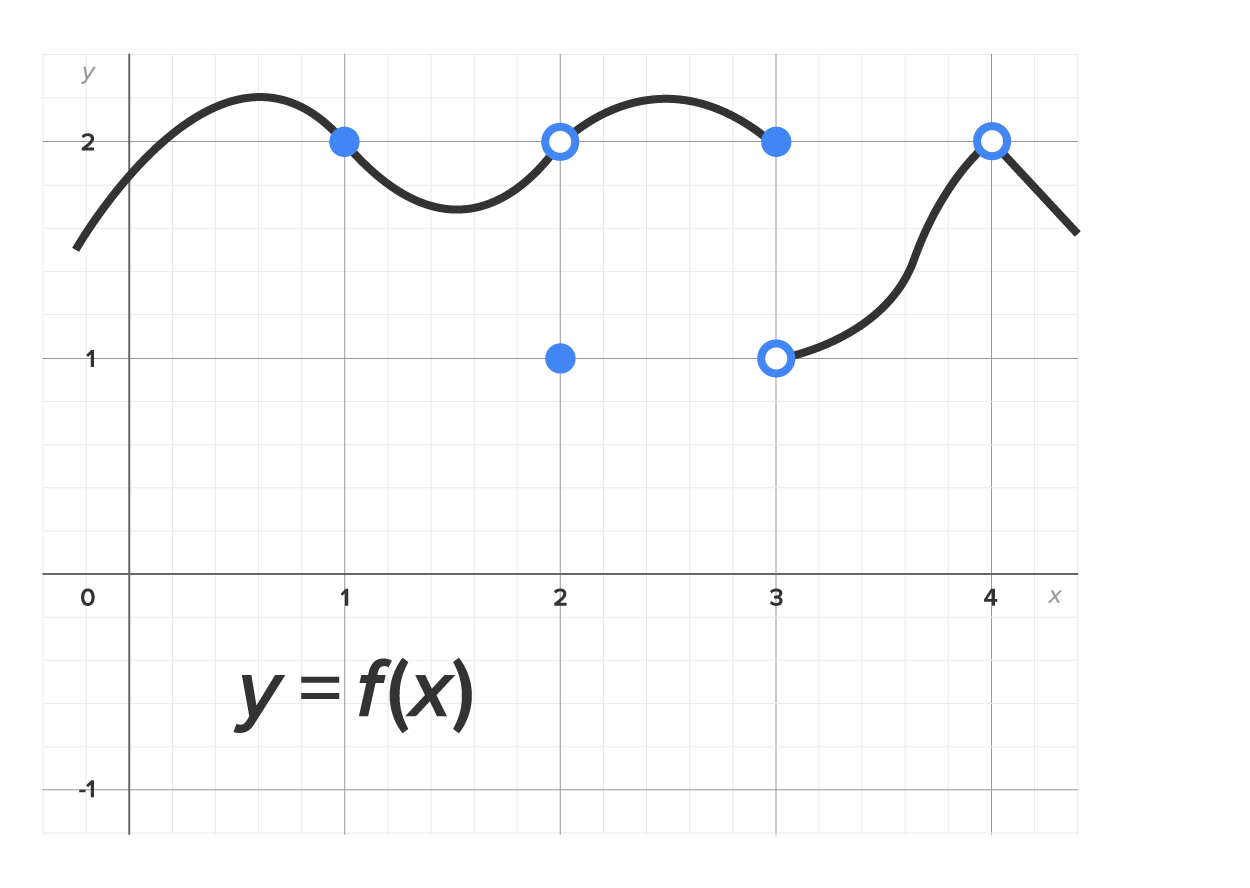
| Given Point |
Continuity of  at the Given Point at the Given Point
|
|---|---|
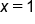
|
The graph of  is continuous when is continuous when 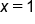 since there are no breaks in the graph at that point. Looking just before since there are no breaks in the graph at that point. Looking just before 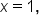 the graph passes through the point the graph passes through the point 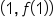 and continues to “flow” afterwards. and continues to “flow” afterwards.
|
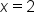
|
The graph of  is NOT continuous when is NOT continuous when 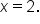 There is a hole in the graph when There is a hole in the graph when 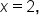 meaning there is a break in the graph. meaning there is a break in the graph.
|
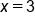
|
The graph is NOT continuous when 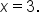 There is a break in the graph. There is a break in the graph.
|
|
The graph is NOT continuous when 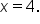 There is a hole in the graph. There is a hole in the graph.
|
Now, considering these 4 points, let’s examine the limits at these points and the values of  at these points as well as whether or not the function is continuous at these points:
at these points as well as whether or not the function is continuous at these points:
| x-value |
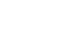
|

|
Continuous? |
|---|---|---|---|
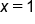
|
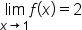
|
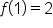
|
Yes |
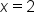
|
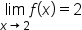
|
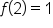
|
No |
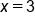
|
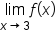 does not exist (the left-hand and right-hand limits are not equal). does not exist (the left-hand and right-hand limits are not equal).
|
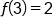
|
No |
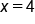
|
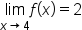
|
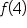 is not defined. is not defined.
|
No |
 is continuous at
is continuous at 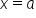 if
if 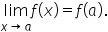 That is,
That is,  exists and is equal to the value of
exists and is equal to the value of 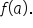
 is not continuous at
is not continuous at 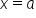 if any of the following occur:
if any of the following occur:  does not exist.
does not exist.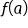 is undefined.
is undefined.  exists, but is not equal to
exists, but is not equal to 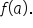
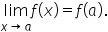
To determine if a function is continuous at 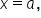 we need to compare the values of
we need to compare the values of  and
and 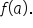 While computing
While computing 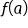 is straightforward, computing
is straightforward, computing  requires more care, and sometimes requires one-sided limits.
requires more care, and sometimes requires one-sided limits.
EXAMPLE
Consider the function . Determine if
. Determine if  is continuous at
is continuous at 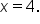
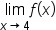 exists. Since
exists. Since  changes definition when
changes definition when 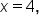 we need to consider the one-sided limits:
we need to consider the one-sided limits:
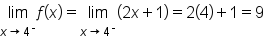
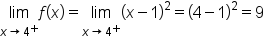
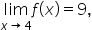 which means it exists and is equal to 9.
which means it exists and is equal to 9. 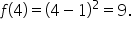 Thus, the limit and the function value are the same; therefore the function is continuous at
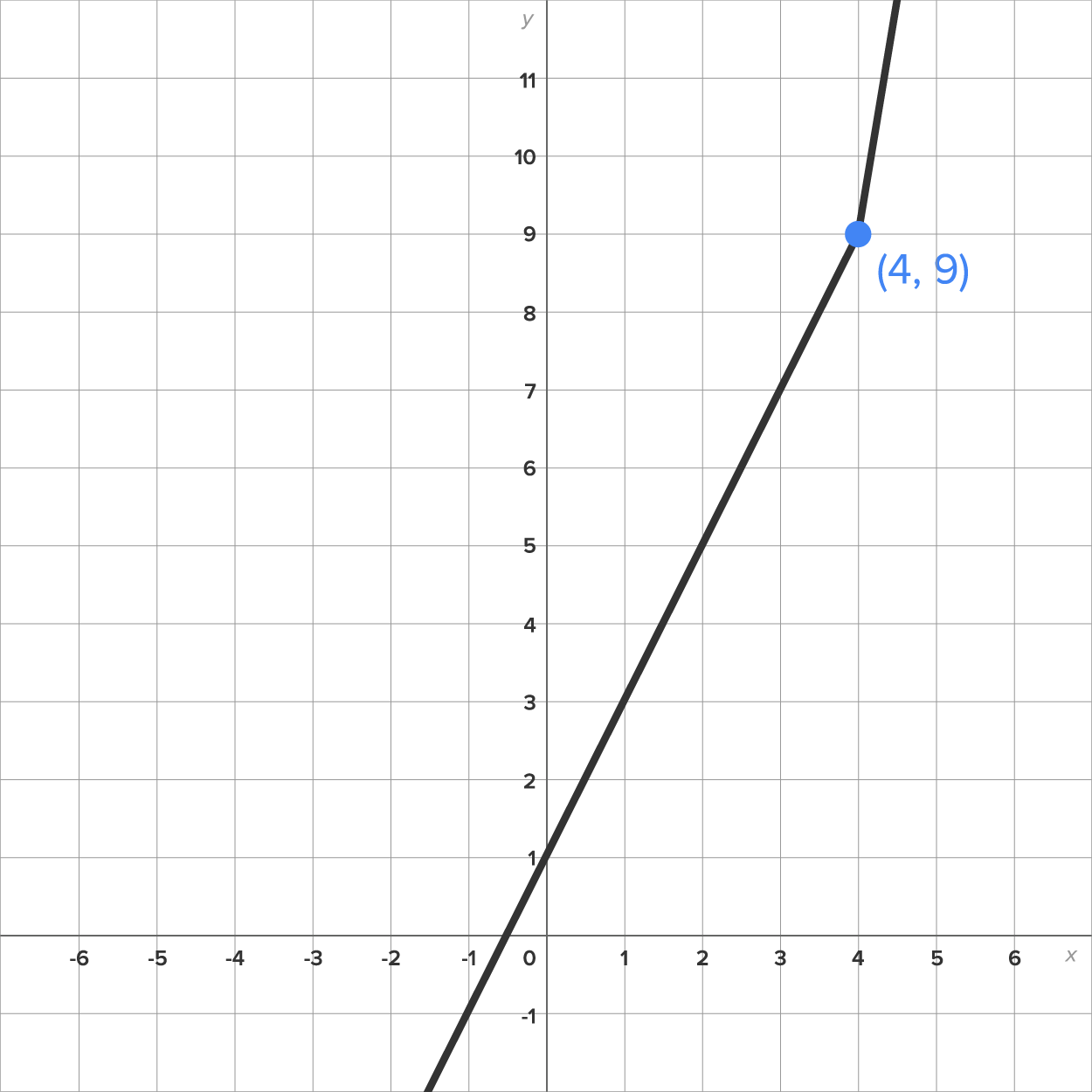
Thus, the limit and the function value are the same; therefore the function is continuous at 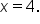 Here is the graph of
Here is the graph of  to help visualize this:
to help visualize this:
EXAMPLE
Consider the function . Determine if
. Determine if  is continuous at
is continuous at 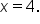
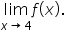 Since
Since  is defined on both sides of
is defined on both sides of 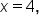 there is no need to compute one-sided limits.
there is no need to compute one-sided limits.
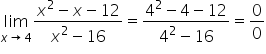
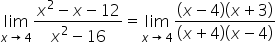
|
Factor the expression. |
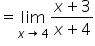
|
Remove the common factor of 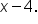
|
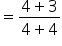
|
Direct substitution works since the denominator is not 0. |
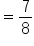
|
Simplify. |
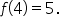 Since the limit and the function value are different, this function is not continuous at
Since the limit and the function value are different, this function is not continuous at 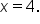 Here is a graph to help visualize this:
Here is a graph to help visualize this:
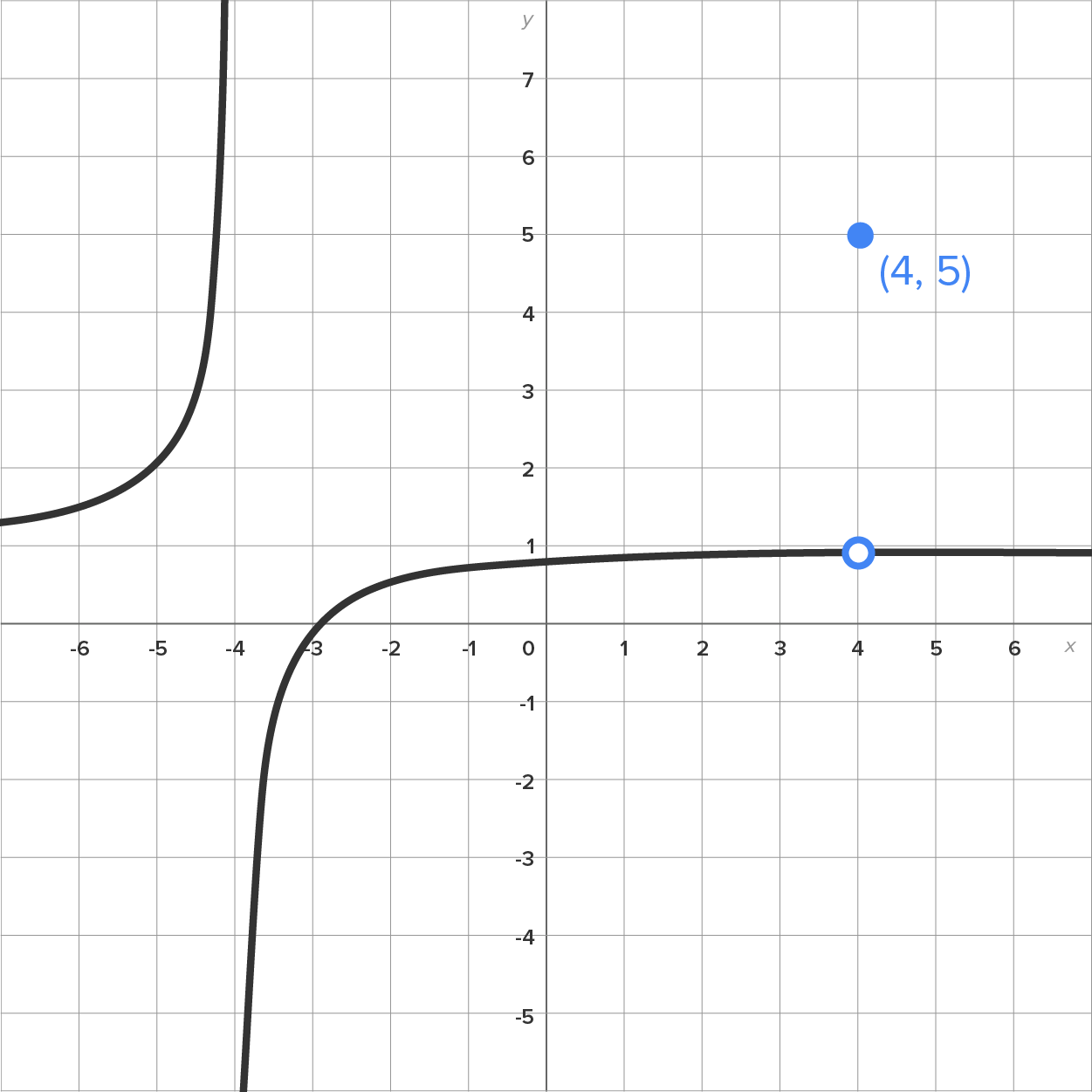
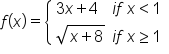
For a function to be continuous on an interval of values, it has to be continuous at every point contained in the interval.
EXAMPLE
 is continuous at every real number. Thus, we say that
is continuous at every real number. Thus, we say that  is continuous on the interval
is continuous on the interval 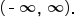
EXAMPLE
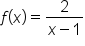 is continuous at every value except
is continuous at every value except 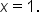 We can say that
We can say that  is continuous on the intervals
is continuous on the intervals 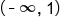 and
and 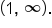 This can also be written as
This can also be written as 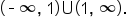
It is also possible to define continuity at an endpoint. For example, consider 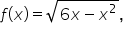 whose graph is shown below. Note that the domain of this function is
whose graph is shown below. Note that the domain of this function is 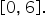
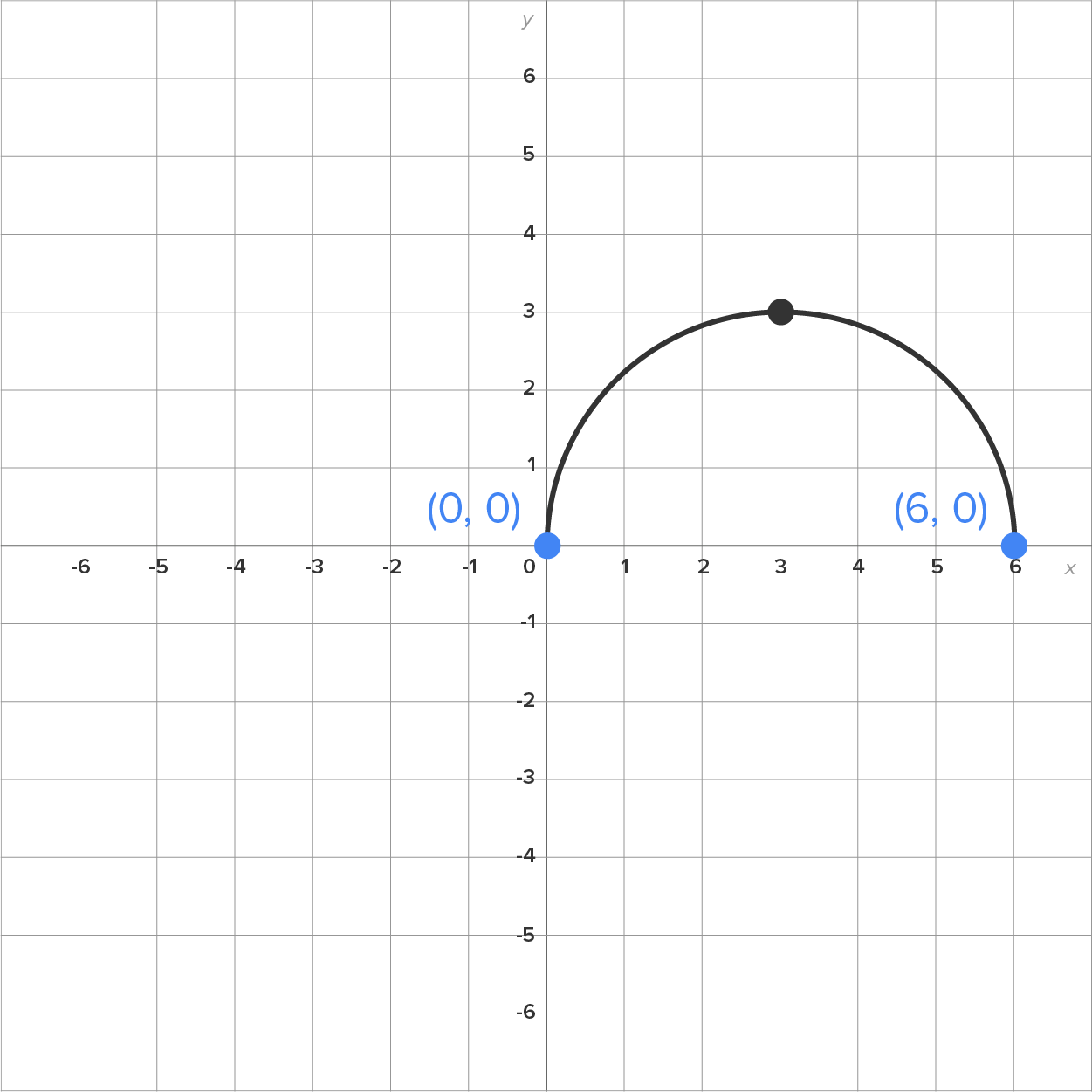
This means that defining continuity at 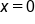 and
and 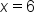 takes a bit more care.
takes a bit more care.
Consider the endpoint 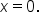 It can only be approached from the right. Looking at the graph, observe that
It can only be approached from the right. Looking at the graph, observe that 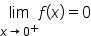 and
and 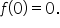
Consider the endpoint 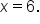 It can only be approached from the left. Looking at the graph, observe that
It can only be approached from the left. Looking at the graph, observe that 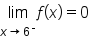 and
and 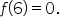
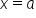 if
if 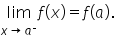
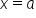 if
if 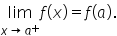
Thus, in the previous problem, we can say that  is continuous from the left at
is continuous from the left at 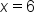 and continuous from the right at
and continuous from the right at 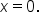 This enables us to say that
This enables us to say that  is continuous for all values on the interval
is continuous for all values on the interval 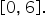
EXAMPLE
Determine the interval(s) over which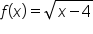 is continuous. The graph is shown below.
is continuous. The graph is shown below.
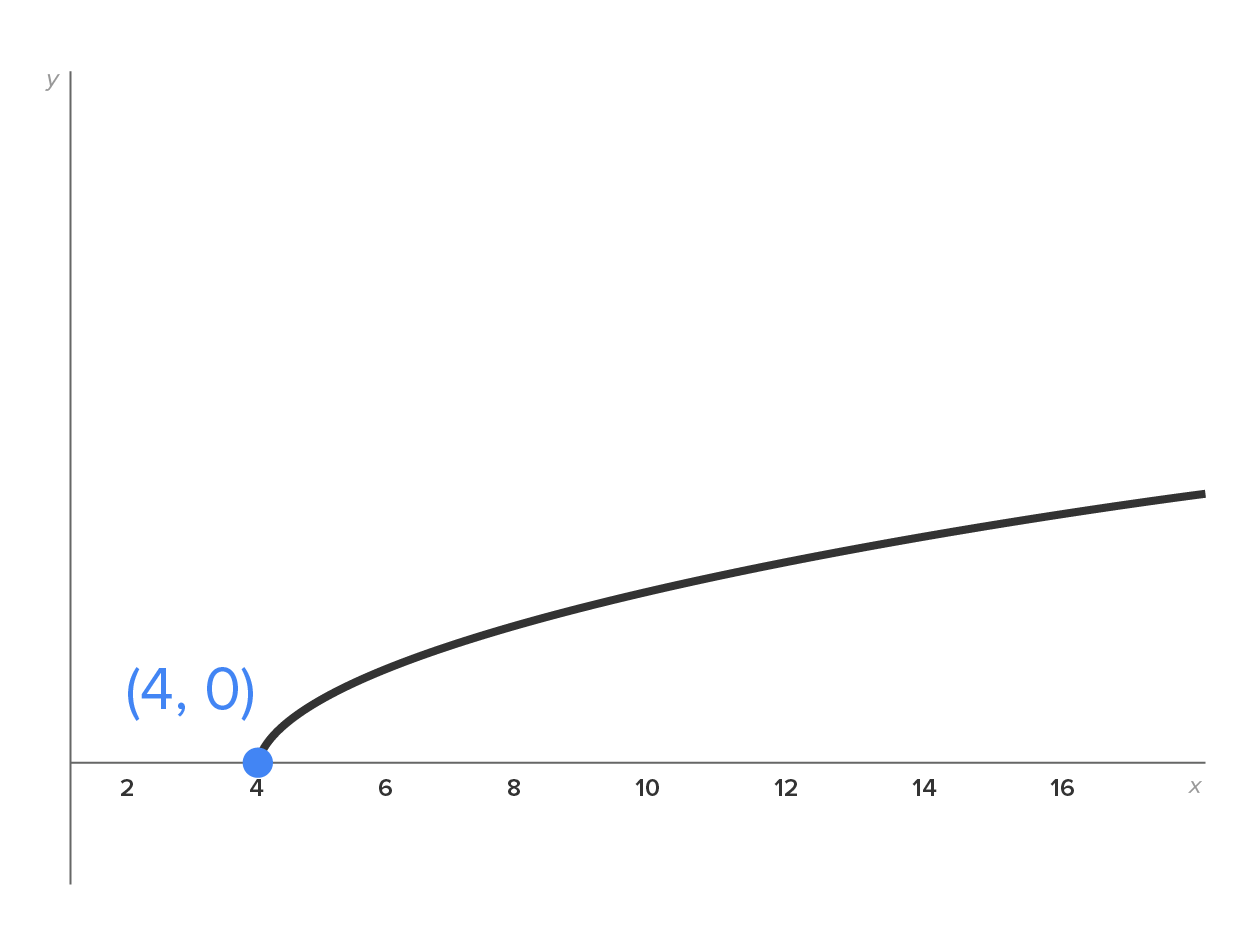
 is
is  It follows that
It follows that  is continuous on the interval
is continuous on the interval 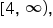 noting that it is continuous from the right at
noting that it is continuous from the right at 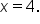
| Function | Continuous Interval |
|---|---|
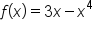
|
? |
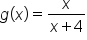
|
? |
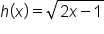
|
? |
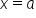 if
if 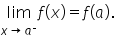
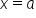 if
if 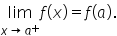
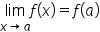 . You learned that you can use limits to determine if a function is continuous at
. You learned that you can use limits to determine if a function is continuous at 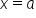 (a specific point) by comparing the values of
(a specific point) by comparing the values of  and
and 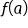 . It's important to note that while computing
. It's important to note that while computing 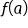 is straightforward, computing
is straightforward, computing  requires more care, and sometimes requires one-sided limits. Lastly, you learned that by examining the domain of a function, you can use it to determine the intervals over which a function is continuous, noting that the function has to be continuous at every point contained in the interval in order to say the function is continuous on the interval.
requires more care, and sometimes requires one-sided limits. Lastly, you learned that by examining the domain of a function, you can use it to determine the intervals over which a function is continuous, noting that the function has to be continuous at every point contained in the interval in order to say the function is continuous on the interval.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 1 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.