Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Conditional Probability with Venn Diagrams

Author: Sophia

what's covered
This tutorial will continue the discussion on the topic of conditional probability.

Table of Contents

1. Conditional Probability With Venn Diagrams

A Venn diagram is a useful tool to visualize conditional probability.

EXAMPLE

What is the probability of getting an even on a roulette wheel? Like the example above, this question is not a conditional probability yet because the question is simply about the probability that the number is even. To find the answer, count up all of the even sectors.
A roulette wheel divided into 38 numbered slots, alternating between black, red, and green colors. The black and red slots are numbered from 1 to 36. The numbers 0 and 00 are placed in green slots exactly opposite to each other. The wheel’s design radiates outward from the center, creating a circular pattern with evenly spaced divisions.

P left parenthesis E v e n right parenthesis equals 18 over 38

hint
Notice that zero and double zero don't count as even. The evens on the roulette wheel are in two categories: even numbers that are in black, and even numbers that are in red. Eighteen of the 38 numbers on the roulette wheel are even.

However, what if we want to know the probability that the sector is even, given that the sector is also black?

This is a conditional probability statement. We can create a Venn diagram to show the relationship between these two characteristics of even and black. Ignore any of the sectors that are neither black nor even, and the ones that are only even without being black. Some of the black numbers are also even.
A Venn diagram inside a rectangle contains two overlapping circles labeled 'E' and 'B.' The section inside circle 'E' only contains the numbers 12, 14, 16, 18, 30, 32, 34, and 36. The overlapping section between 'E' and 'B' contains the numbers 2, 4, 6, 8, 10, 20, 22, 24, 26, and 28. The section inside circle 'B' only contains the numbers 11, 13, 15, 17, 29, 31, 33, and 35. Outside both circles are the numbers 0, 1, 3, 5, 7, 9, 19, 21, 23, 25, 27, and 00.
Of the 18 numbers that are black on the roulette wheel, 10 selections are both even and black. So, the probability is 10 even black sectors out of 18 total black sectors.

We could also use the conditional probability formula, which states we need to find the probability of a sector being both even and black, which is 10 out of 38, and divide by the probability of a sector being black, which is 18 out of 38.
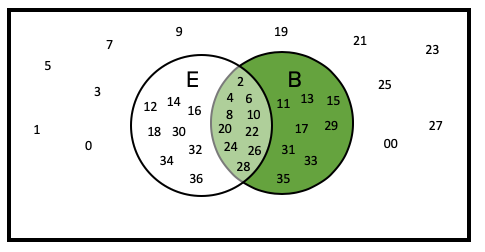
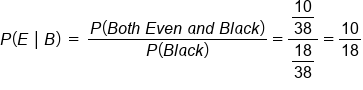
P left parenthesis E space vertical line space B right parenthesis space equals space fraction numerator P left parenthesis B o t h space E v e n space a n d space B l a c k right parenthesis over denominator P left parenthesis B l a c k right parenthesis end fraction equals fraction numerator begin display style 10 over 38 end style over denominator begin display style 18 over 38 end style end fraction equals 10 over 18


In the example above, we show all the individual members of each group, but usually Venn diagrams summarize this by only indicating the total number of individuals in that group, as in the example below.

try it
A Venn diagram with two overlapping circles. The left circle is labeled ‘Vanilla’ and contains the number 28. The right circle is labeled ‘Chocolate’ and contains the number 16. The overlapping section between the circles contains the number 22, representing those who like both vanilla and chocolate. The total number of people surveyed is indicated by the number 34 below the diagram.
The Venn diagram represents the protein powder flavor preferences of 100 bodybuilders.
What is the probability that a bodybuilder likes chocolate protein powder, given we know they like vanilla?
Apply the conditional probability formula. P left parenthesis C h o c o l a t e vertical line V a n i l l a right parenthesis space equals space fraction numerator P left parenthesis V a n i l l a space a n d space C h o c o l a t e right parenthesis over denominator P left parenthesis V a n i l l a right parenthesis end fraction
P left parenthesis C h o c o l a t e vertical line V a n i l l a right parenthesis space equals space fraction numerator 0.22 over denominator 0.50 end fraction space equals space 0.44 space o r space 44 percent sign space
hint
To calculate P(vanilla), be sure to count both the 28 who like vanilla only and the 22 who like both flavors.
(28/100 + 22/100 = 0.50)

summary
Conditional probability is the probability of some second event occurring, given that some first event has already occurred. It's calculated by dividing the joint probability of the two events by the probability of the existing event (the one that's already happening). This formula works for all events. This isn't a special formula that works only for independent events or only for mutually exclusive events. As you explored in this lesson, it is helpful to visualize conditional probability with Venn diagrams.

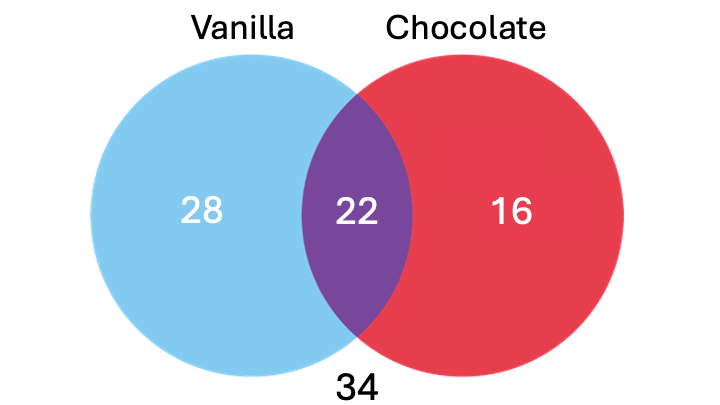
Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

© 2026 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.