Table of Contents |
Concavity refers to the direction in which a graph opens. A graph is concave up if it opens upward and concave down if it opens downward. A graph is concave up on an interval if it opens upward on that interval. A graph is concave down on an interval if it opens downward on that interval.
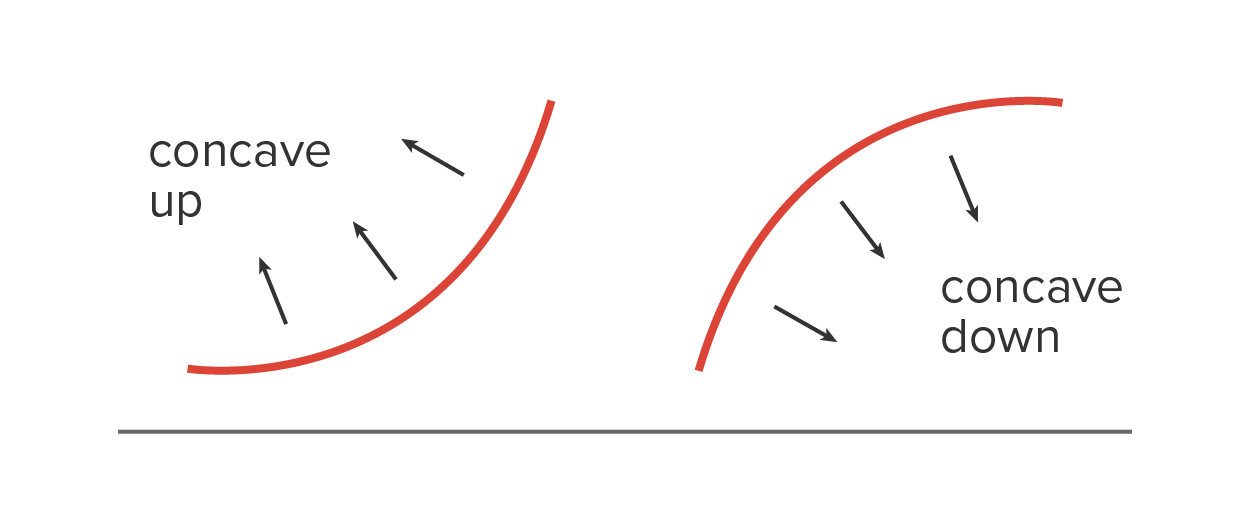
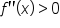 on an interval, then the graph of
on an interval, then the graph of  is concave up on the same interval.
is concave up on the same interval. 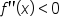 on an interval, then the graph of
on an interval, then the graph of  is concave down on the same interval.
is concave down on the same interval.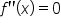 or
or  is undefined. Then, make a sign graph similar to what you did for the first derivative test.
is undefined. Then, make a sign graph similar to what you did for the first derivative test.
EXAMPLE
Determine the interval(s) over which the graph of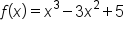 is concave up or concave down. Since concavity is determined from the second derivative, we start there.
is concave up or concave down. Since concavity is determined from the second derivative, we start there.
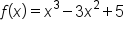
|
Start with the original function. |
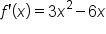
|
Take the first derivative. |
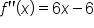
|
Take the second derivative. |
 is never undefined, we set it to 0 and solve:
is never undefined, we set it to 0 and solve:
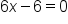
|
The second derivative is set to 0. |
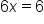
|
Add 6 to both sides. |
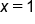
|
Divide both sides by 6. |
 could be changing concavity when
could be changing concavity when 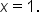 This means that at any x-value on the interval
This means that at any x-value on the interval 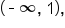 the concavity is the same. The same can be said for the interval
the concavity is the same. The same can be said for the interval 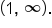
 on that interval:
on that interval:
| Interval |
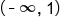
|
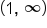
|
|---|---|---|
| Test Value | 0 | 2 |
Value of 
|
-6 | 6 |
Behavior of 
|
Concave down | Concave up |
 is concave down on the interval
is concave down on the interval 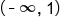 and concave up on the interval
and concave up on the interval 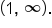
EXAMPLE
Determine the interval(s) over which the graph of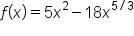 is concave up or concave down. Note that the domain of
is concave up or concave down. Note that the domain of  is all real numbers.
is all real numbers.
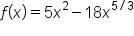
|
Start with the original function. |
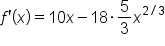 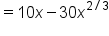
|
Take the first derivative. |
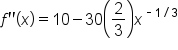 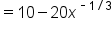 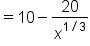
|
Take the second derivative. |
 is undefined when
is undefined when 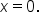
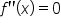 and solve:
and solve:
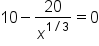
|
The second derivative is set to 0. |
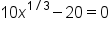
|
Multiply everything by 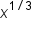 . .
|
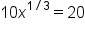
|
Add 20 to both sides. |
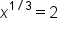
|
Divide both sides by 10. |
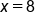
|
Cube both sides. |
 could be changing concavity when
could be changing concavity when 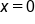 or
or 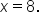 This means that at any x-value on the interval
This means that at any x-value on the interval 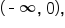 the concavity is the same. The same can be said for the intervals
the concavity is the same. The same can be said for the intervals 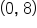 and
and 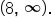
 on that interval:
on that interval:
| Interval |
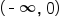
|
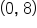
|
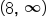
|
|---|---|---|---|
| Test Value | -1 | 1 | 27 |
Value of 
|
30 | -10 |
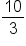
|
Behavior of 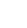
|
Concave up | Concave down | Concave up |
 is concave up on
is concave up on 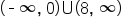 and concave down on the interval
and concave down on the interval 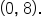
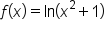 is concave up or concave down.
is concave up or concave down.
Here is a problem for you to try, step by step. This will also help you review some algebra skills.
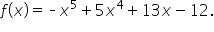
 .
.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.