Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Compound Interest

Author: Sophia
PDF Version

what's covered
In this lesson, we will continue to explore interest by looking at compound interest. You will continue strengthening your results driven skill as you solve problems involving compound interest. Specifically, we will discuss:

Table of Contents

1. Simple Interest vs. Compound Interest

As we discussed in our last lesson, there are two different types of interest: simple interest and compound interest. Simple interest is, well, simple to figure out with a simple formula of:

formula to know
Simple Interest
table attributes columnalign left end attributes row cell I equals P times r times t end cell row cell where colon end cell row cell I equals Interest end cell row cell P equals Principal end cell row cell r equals Rate space left parenthesis decimal right parenthesis end cell row cell t equals Time space left parenthesis years right parenthesis end cell end table

Simple interest assumes that the interest amount toward a loan or investment is not added back into the principal. Additionally, the time is calculated in years.

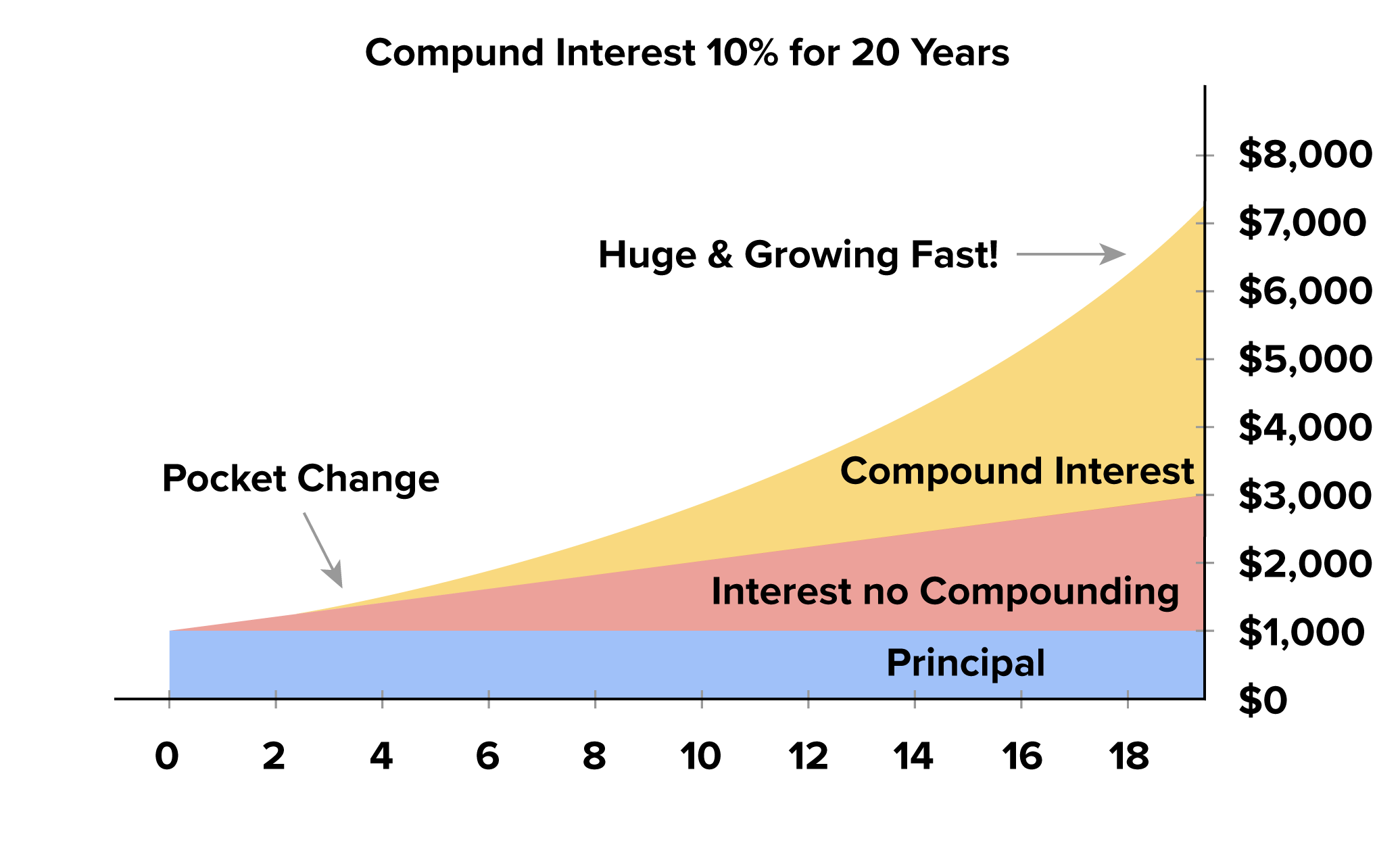
Unlike simple interest, compound interest assumes that the interest earned or incurred is added to the principal amount at set intervals like daily, weekly, monthly, or yearly. Of course, this means that the amount earned in interest becomes much higher.

Let’s look at the power of compound interest over simple interest.

  • If you keep $1,000 in a piggy bank, you’ll still have $1,000 at the end of 20 years.
  • If you invest $1,000 with 10% simple interest, you’ll have about $3,000 at the end of 20 years.
  • If you invest $1,000 with 10% compound interest, you’ll have over $7,000 at the end of 20 years.
A graph depicting the growth of compound interest over time. The x-axis represents time, ranging from 0 to 20 years. The y-axis represents the amount of money, ranging from $0 to $8,000. The graph is divided into three sections, with ‘Principle’ at $1,000, ‘Interest no Compounding’ at $3,000, and ‘Compound Interest’ at $7,000. The graph shows an exponential increase in the total amount because of compounding. An arrow pointing to the start of the compound interest section is labeled ‘Pocket Change’, and another arrow pointing to the peak of the compound interest section is labeled ‘Huge & Growing Fast!’.

Results Driven: Skill Reflect
Consider whether you currently have any accounts that use compound interest. Before this lesson, did you know whether the interest in that account was simple or compound? Consider how you can use this information to better plan how much money you save in the long run. By doing this, you will be strengthening your results driven skill.

term to know
Compound Interest
Interest calculated on the original amount and the interest earned or incurred.

2. Calculating Compound Interest

You will use the following equation for compound interest:

formula to know
Compound Interest
table attributes columnalign left end attributes row cell A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent end cell row cell where colon end cell row cell A equals Total space amount space earned end cell row cell P equals Principal end cell row cell r equals Rate space left parenthesis decimal right parenthesis end cell row cell n equals Number space of space times space interest space is space applied space per space year end cell row cell t equals Time space left parenthesis years right parenthesis end cell end table

In this formula, A is the total amount earned at a give time (t), P is the principal or starting amount, r is the interest rate (as a decimal), t is the time (in years), and n is the number of times interest is applied per year.

Note that the equation for compound interest will result in the total amount earned at the end of time, t. This will be the principal amount and the interest earned added together. The n in the equation represents the number of times interest is applied per year. This would be a whole number such as 1, 2, 4, etc. There are some commonly used words to describe the number of times interest is applied. Looking at the table below we see, for example, if interest is compounded quarterly, this means that interest is applied every 3 months or 4 times of the year. The n in the equation would be 4.

The following table shows commonly used wording to describe the number of time interest is applied within a year:

Wording n (# of times interest is applied)
Annually 1
Semiannually 2
Quarterly 4
Monthly 12
Weekly 52
Daily 365

If you see wording in the above table, you can quickly determine the number of times interest will be applied per year.

hint
Calculating compound interest uses mathematical computations we have already covered such as fractions, exponents, and order of operations.

EXAMPLE

Martin has a credit card which he has maxed out at $10,000. Unfortunately, he cannot make any payments. Assuming he pays a 15% interest rate, compounded daily, how much will Martin owe in one year?

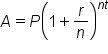
A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent Compound Interest Formula
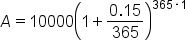
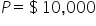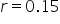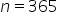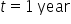
A equals 10000 open parentheses 1 plus fraction numerator 0.15 over denominator 365 end fraction close parentheses to the power of 365 times 1 end exponent Substitute the known values: P equals $ 10 comma 000, r equals 0.15 (15% as a decimal), n equals 365 (compounded daily), t equals 1 space year
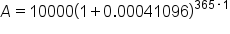
A equals 10000 open parentheses 1 plus 0.00041096 close parentheses to the power of 365 times 1 end exponent To solve this equation, we must use the order of operations. We will start with what is inside the parentheses. Division within the parenthesis comes first.
A equals 10000 left parenthesis 1.00041096 right parenthesis to the power of 365 times 1 end exponent Next, evaluate the addition inside the parentheses.
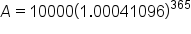
A equals 10000 left parenthesis 1.00041096 right parenthesis to the power of 365 Complete the multiplication in the exponent.
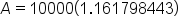
A equals 10000 left parenthesis 1.161798443 right parenthesis Apply the exponent.
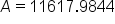
A equals 11617.9844 Multiply the remaining values.

Martin will owe a total of $11,617.98 after one year. Ouch!

EXAMPLE

Maryanne is going to invest $5,000 in a retirement account that compounds 10% monthly. If she invests when she’s 25 and retires at the age of 65, how much will she have in the account?

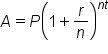
A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent Compound Interest Formula
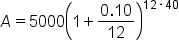
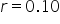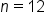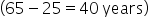
A equals 5000 open parentheses 1 plus fraction numerator 0.10 over denominator 12 end fraction close parentheses to the power of 12 times 40 end exponent Substitute the known values: P equals $ 5 comma 000, r equals 0.10 (10% as a decimal), n equals 12 (compounded monthly), t equals 40 open parentheses 65 minus 25 equals 40 space years close parentheses
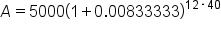
A equals 5000 open parentheses 1 plus 0.00833333 close parentheses to the power of 12 times 40 end exponent To solve this equation, we must use the order of operations. We will start with what is inside the parentheses. Division within the parenthesis comes first.
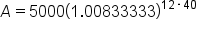
A equals 5000 open parentheses 1.00833333 close parentheses to the power of 12 times 40 end exponent Next, evaluate the addition inside the parentheses.
A equals 5000 open parentheses 1.00833333 close parentheses to the power of 480 Complete the multiplication in the exponent.
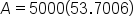
A equals 5000 left parenthesis 53.7006 right parenthesis Apply the exponent.
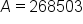
A equals 268503 Multiply the remaining values.

Maryann will have $268,503 after 40 years. Wow. Start investing early!

try it
Gianna has found her dream home for $250,000.
How much will she pay at the end of a 30-year loan if she can secure a 4.5% interest rate that compounds monthly?
A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent Compound Interest Formula
A equals $ 250 comma 000 open parentheses 1 plus fraction numerator 0.045 over denominator 12 end fraction close parentheses to the power of 12 cross times 30 end exponent Substitute the known values: P equals $ 250 comma 000, r equals 0.045 (4.5% as a decimal), n equals 12 (compounded monthly), t equals 30
$ 961 comma 924.51 Evaluate

Gianna will pay a total of $961,924.51 for her dream house by the time she has paid off her mortgage.

try it
Maurice wants to save up for a down payment on a new car. Suppose he invests $2,000 in a savings account at 6% interest compounded weekly for one year.
How much will he have earned after one year?
A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent Compound Interest Formula
A equals $ 2 comma 000 open parentheses 1 plus fraction numerator 0.06 over denominator 52 end fraction close parentheses to the power of 52 cross times 1 end exponent Substitute the known values: P equals $ 2 comma 000, r equals 0.06 (6% as a decimal), n equals 52 (compounded weekly), t equals 1 space year
$ 2 comma 123.60 Evaluate

Maurice will have a total of $2,123.60 after one year.

summary
In this lesson, we continued our exploration into interest. We learned the difference between simple interest versus compound interest is that compound interest grows the reinvested interest amount substantially more than simple interest rates. We also calculated compound interest using the compound interest formula. Finally, you discovered how calculating compound interest helps you meet your financial goals, strengthening your results driven skill.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Terms to Know
Compound Interest

Interest calculated on the original amount and the interest earned or incurred. 

Formulas to Know
Compound Interest

A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent where colon A equals Total space amount space earned P equals Principal r equals Rate space left parenthesis decimal right parenthesis n equals Number space of space times space interest space is space applied space per space year t equals Time space left parenthesis years right parenthesis

Simple Interest

I equals P times r times t where colon I equals Interest P equals Principal r equals Rate space left parenthesis decimal right parenthesis t equals Time space left parenthesis years right parenthesis

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.