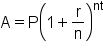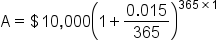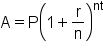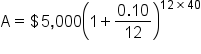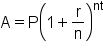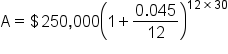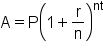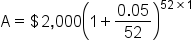In this lesson, we will continue to explore interest by looking at compound interest. You will continue strengthening your results driven skill as you solve problems involving compound interest. Specifically, we will discuss:
- Simple Interest Versus Compound Interest
- Calculating Compound Interest
1. Simple Interest Versus Compound Interest
As we discussed in our last lesson, there are two different types of interest: simple interest and compound interest. Simple interest is, well, simple to figure out with a simple formula of:
-
-
- Simple Interest
-
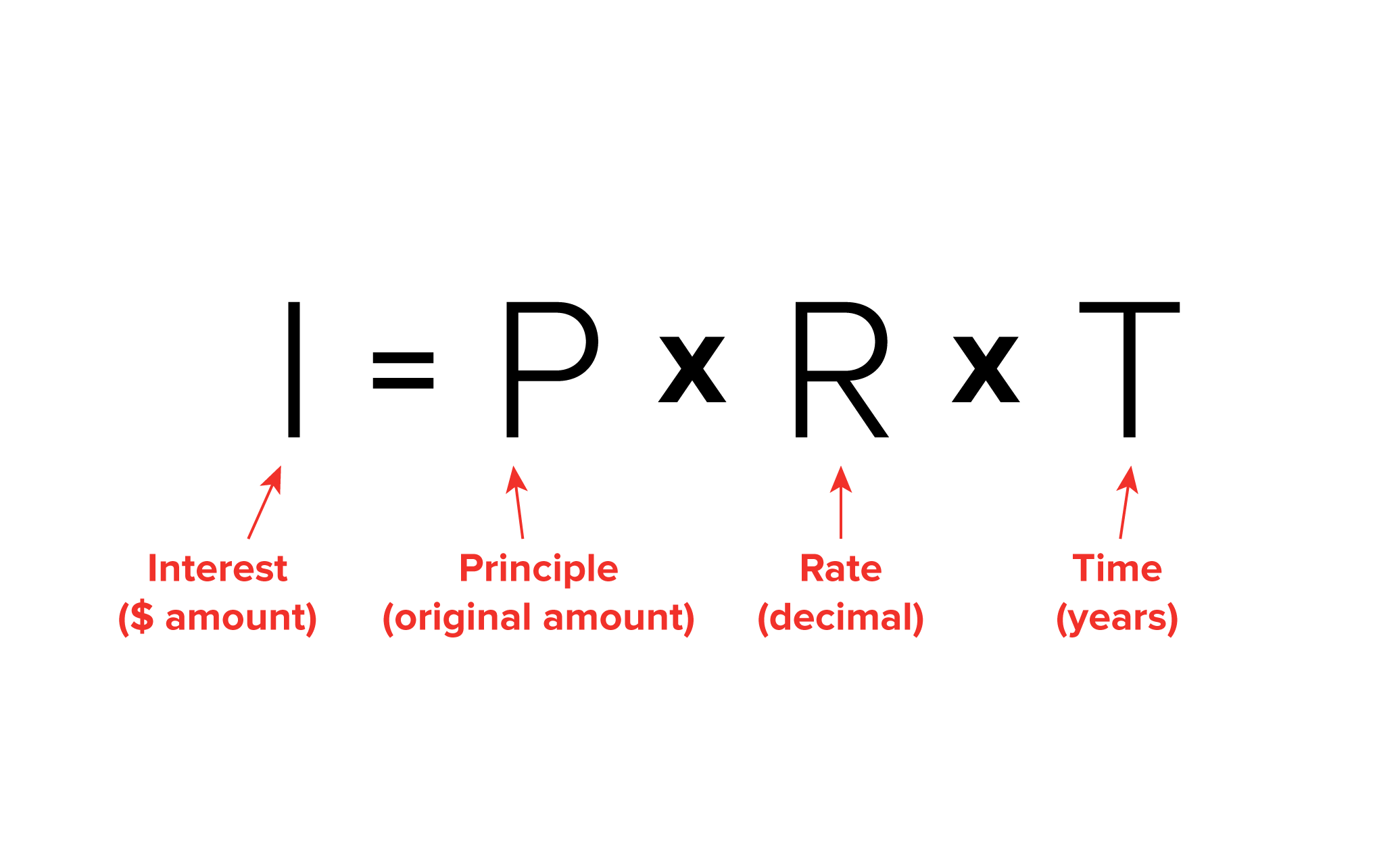
Simple interest assumes that the interest amount toward a loan or investment is not added back into the principle. Additionally, the time is calculated in years.
Unlike simple interest, compound interest assumes that the interest earned or incurred is added to the principle amount at set intervals like daily, weekly, monthly, or yearly. Of course, this means that the amount earned in interest becomes much higher.
-
-
- Compound Interest
-
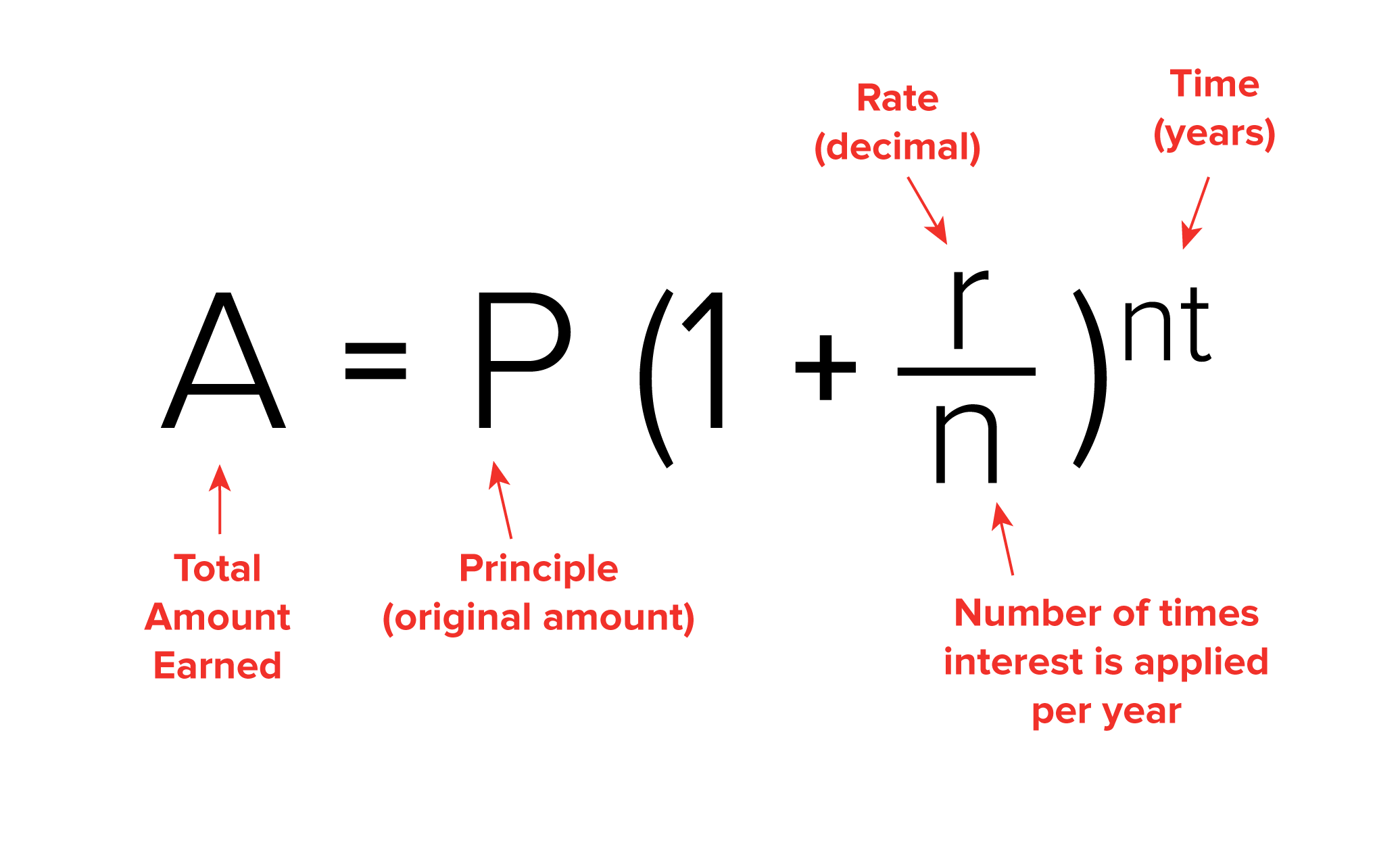
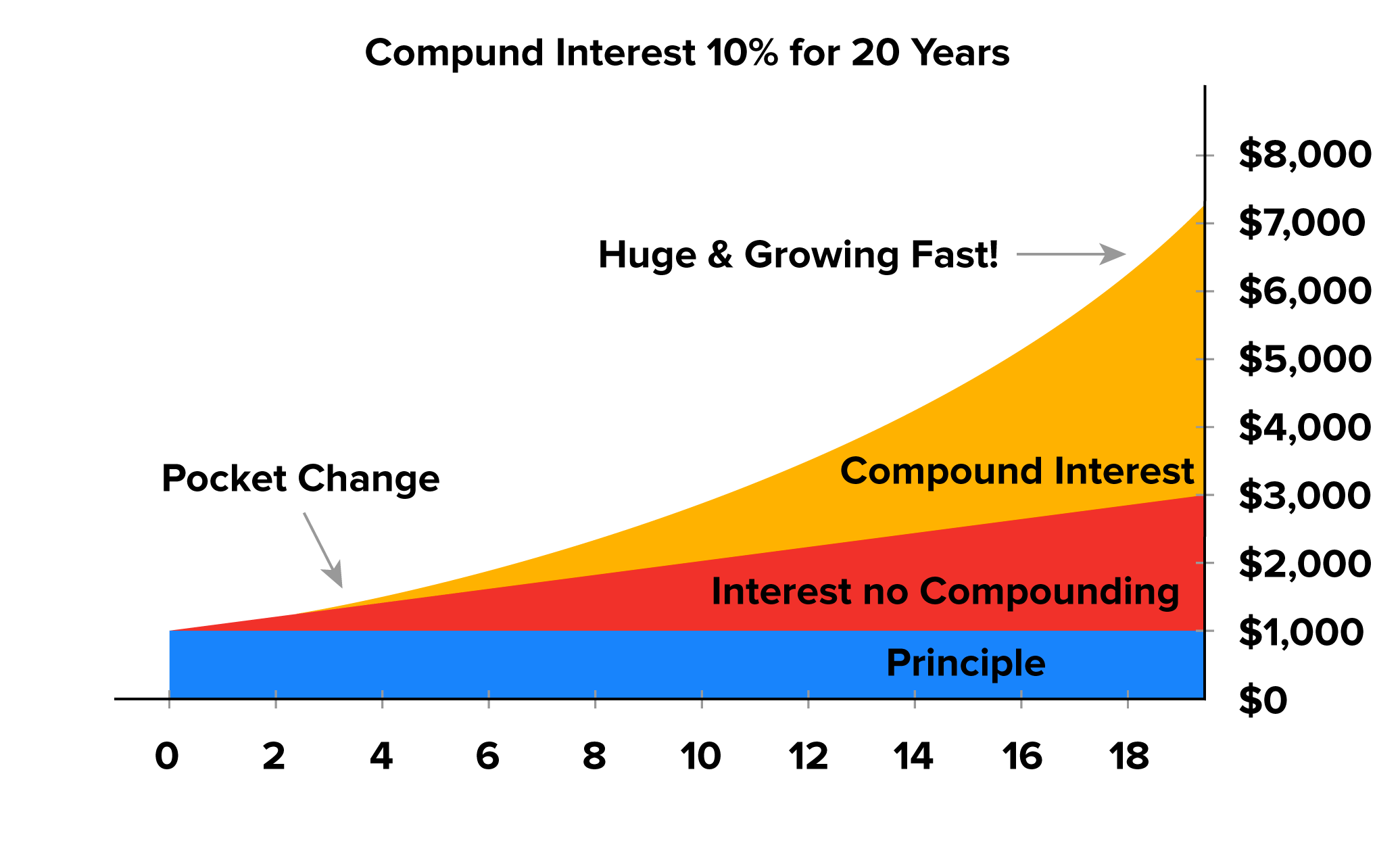
Let’s look at the power of compound interest over simple interest.
If you keep $1,000 in a piggy bank, you’ll still have $1,000 at the end of 20 years.
If you invest $1,000 with 10% simple interest, you’ll have about $3,000 at the end of 20 years.
If you invest $1,000 with 10% compound interest, you’ll have over $7,000 at the end of 20 years.
2. Calculating Compound Interest
Although calculating compound interest by hand uses mathematical computations we have already covered such as fractions, exponents, and order of operations, completing the arithmetic is a lengthy process.
The good news is that there are many compound interest calculators that can be found online. Do an internet search for “compound interest calculator” and choose your favorite site for the examples below. Make sure to carefully read the fields on your chosen calculator. For example, many ask for the percent as a percentage, not the decimal equivalent.
Consider whether you currently have any accounts that use compound interest. Before this lesson, did you know whether the interest in that account was simple or compound? Consider how you can use this information to better plan how much money you save in the long run. By doing this, you will be strengthening your results driven skill.
-
EXAMPLE
Martin has a credit card which he has maxed out at $10,000. Unfortunately, he cannot make any payments. Assuming he pays a 15% interest rate, compounded daily, how much will Martin owe in one year?
Let’s set up our formula so we know what to put into our compound interest calculator.
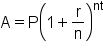
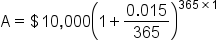
Martin will owe a total of $11,617.94 after one year. Ouch!
-
Fields for Online Compound Interest Calculator
Initial Deposit: $10,000
Additional Contributions: 0
Length of Time in Years (Time Span): 1 year
Estimated Interest Rate: 15 (or 15%)
Compound Frequency: Daily
-
EXAMPLE
Maryanne is going to invest $5,000 in a retirement account that compounds 10% monthly. If she invests when she’s 25 and retires at the age of 65, how much will she have in the account?
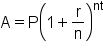
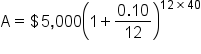
Maryann will have $268,503.32. Wow. Start investing early!
-
Gianna has found her dream home. How much interest will she pay at the end of a 30-year loan if she can secure a 4.5% interest rate that compounds monthly for the $250,000 home?
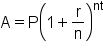
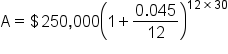
Gianna will pay a total of $961,924.51 for her dream house by the time she has paid off her mortgage.
-
Maurice wants to save up for a down payment on a new car. If he invests $2,000 in a savings account at 6% interest compounded weekly for one year, how much will he have earned in interest?
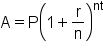
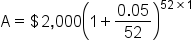
Maurice will have a total of $2,123.60 after one year.
In this lesson, we continued our exploration into interest. We learned the difference between simple interest versus compound interest is that compound interest grows the reinvested interest amount substantially more than simple interest rates. We also calculated compound interest using online resources after setting up our compound interest formula, although this arithmetic can be done by hand as well using the principles of order of operations, fractions, and exponents. Finally, you discovered how calculating compound interest helps you meet your financial goals, strengthening your results driven skill.
Best of luck in your learning!