In this lesson, you will learn how to solve for account balance by using the compound interest formula. Specifically, this lesson will cover:
1. Compound Interest
1a. Interest Compounded Once Per Year
Financial accounts appreciate in value according to an annual interest rate, which we typically refer to as APR (annual percentage rate). When using the APR to calculate account balances with interest, we always express the percentage as a decimal.
-
EXAMPLE
A 5% APR would be expressed as 0.05.
If interest is applied once per year, we say that interest is compounded annually. This means that each year when interest is added, the amount of interest earned is not only based on the original investment, but any interest that has already been earned previously.
-
EXAMPLE
Suppose that $2000 is invested into an account that pays an APR of 5%. If interest is added just once per year, then the final account balance after one year is
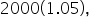
or $2100.
If we want the balance after two years, we can approach this in two ways:
We can multiply $2100 by another factor of 1.05, which gives
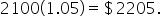
For another way, think about how we get this result from the starting balance.
To get the balance after one year, multiply
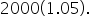
To get the balance after one more year, multiply by another (1.05). This gives
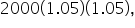
or
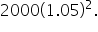
If you evaluate this, you also get $2205.
To find the account balance after three years, we would compute
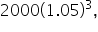
and would get $2315.25.
This leads to a formula that can be used to find the final account balance with any starting balance, APR, and number of years.
-
- Compound Interest, Interest Compounded Annually
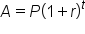
In this formula,
-
A is the account balance after t number of years.
-
P is the principal balance (initial starting value).
-
r is the APR, expressed as a decimal.
-
t is time in years.
1b. Interest Earned Several Times Per Year
Many accounts gather interest several times per year, not just once. This is compounding interest. When interest is compounded, a portion of the APR is applied throughout the year.
- If interest is compounded twice a year, half of the APR is applied mid-year, and the other half is applied at the end of the year.
- If interest is compounded quarterly, one-fourth of the APR is applied every three months, for a total of four times per year.
- If interest is compounded monthly, one-twelfth of the APR is applied each month, for a total of 12 times per year.
We need to adjust our interest formula to account for compounding interest. To do so, we introduce a new variable,
n, which represents the number of times per year interest is compounded. How does
n affect our formula? It divides
r, the annual percentage rate, and it must also be multiplied by
t, since it represents the number of times
per year that interest is compounded.
Our formula for compounding interest is:
-
- Compound Interest
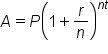
In this formula:
-
A is the account balance after t number of years.
-
P is the principal balance (initial starting value).
-
r is the APR, expressed as a decimal.
-
t is the number of years.
-
n is the number of times per year interest is compounded.
2. Solving for Account Balance
Now that we have a formula to work with, we can use this formula to answer questions about account balances, provided we have information about APR and how many times per year the interest is compounded. Consider the following scenario asking us to find the balance of an account after a certain time period.
-
EXAMPLE
A checking account has an initial balance of $800.00. The account gains 3.5% interest, which is compounded monthly. What is the value of the account after 4 years, assuming no additional withdrawals or deposits are made?
First, we need to write down the values of as many variables as possible, based on the information provided to us.
-
P: We know that the starting balance of the account is $800.00, so P is 800.
-
r: Our annual percentage rate is 3.5%, which as a decimal is 0.035.
-
n: Interest is compounded monthly, so n will be 12.
-
t: We need to find the account balance after 4 years, so t is 4.
The account balance,
A, remains unknown.
Fitting these into our formula, we get:
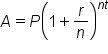
|
Plug in 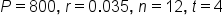
|
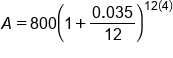
|
Evaluate the division in the parentheses
|
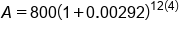
|
Simplify the parentheses
|
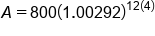
|
Evaluate exponent
|
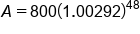
|
Apply exponent
|
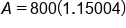
|
Multiply
|
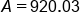
|
Our solution, rounded to the nearest cent
|
The account balance will be $920.03 after 4 years.
-
Follow the order of operations! Evaluate inside the parentheses first, then apply the exponent, and finally multiply by the principal value.
3. Solving for Growth Time
In this next sample, we are going to see how to apply logarithms to solve for the variable time, t.
-
EXAMPLE
Using the same account from above, that has an initial balance of $800.00 with 3.5% interest compounding monthly. We would like to know how many years it will take for the account balance to double.
When the account balance doubles, our
A value will equal 1600. We still have 800 for
P, 0.035 for
r, and 12 for
n. What we don't know is the time,
t:
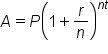
|
Plug in 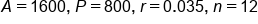
|
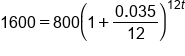
|
Simplify parentheses
|

|
Divide both sides by 800
|
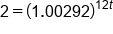
|
Solve for t
|
We were able to simplify this formula a bit before we worry about solving for
t. We cleaned up what was inside the parentheses first. Then, we divided by 800, because the exponent is attached to the fraction, not the 800. Once we divided by 800, we get 2 on the left side of the equation (which represents the account doubling in value) and an expression with our variable,
t, in the exponent on the right side.
To undo the variable exponent, we apply a logarithm to both sides. It doesn't matter in this case if you use the common log or the natural log. Whichever logarithm you prefer will work just fine. When we take the log of both sides, we'll need to apply the Power Property of Logs to isolate our variable
t. This property allows us to move the variable from an exponent within the log to a coefficient outside of the log. Once we do that, we can isolate
t by dividing by everything else on that side.
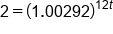
|
Take log of both sides
|
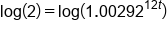
|
Apply Power Property of Logs
|
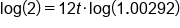
|
Divide both sides by 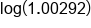
|
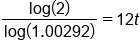
|
Use a calculator to evaluate the division on the left side
|
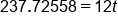
|
Divide both sides by 12
|

|
Our solution
|
This means it will take 19.81 years, or almost 20 years, for the account to double, given our assumptions of rate of growth.
Annual interest can be found using the formula
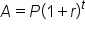
. In the
compound interest formula,
A is the account balance,
P is the principal,
r is the annual interest rate,
n is the number of times per year that the interest is compounded, and
t is the time in years. Compounding interest means that a portion of the annual interest rate is applied throughout the year. When
solving for the account balance, we are solving for the variable
A. When
solving for the growth time, we are solving for the variable
t and will need to apply a logarithm.
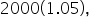 or $2100.
or $2100.
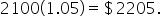
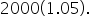
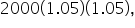 or
or 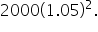 If you evaluate this, you also get $2205.
If you evaluate this, you also get $2205.
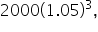 and would get $2315.25.
and would get $2315.25.
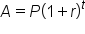
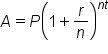
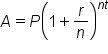
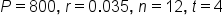
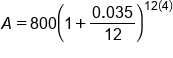
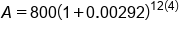
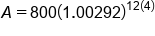
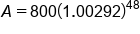
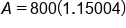
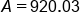
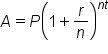
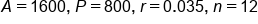
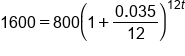

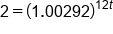
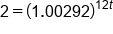
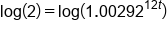
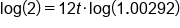
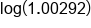
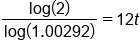
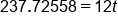

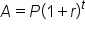 . In the compound interest formula, A is the account balance, P is the principal, r is the annual interest rate, n is the number of times per year that the interest is compounded, and t is the time in years. Compounding interest means that a portion of the annual interest rate is applied throughout the year. When solving for the account balance, we are solving for the variable A. When solving for the growth time, we are solving for the variable t and will need to apply a logarithm.
. In the compound interest formula, A is the account balance, P is the principal, r is the annual interest rate, n is the number of times per year that the interest is compounded, and t is the time in years. Compounding interest means that a portion of the annual interest rate is applied throughout the year. When solving for the account balance, we are solving for the variable A. When solving for the growth time, we are solving for the variable t and will need to apply a logarithm.