Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Composition of Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will find compositions of functions. Specifically, this lesson will cover:

Table of Contents

1. The Definition of a Composition of Functions

Sometimes it is useful to use one function to get a result, then use that result in another function. This idea is called composition of functions.

Here is a picture to show how this works:

A mathematical composition represented by three ovals connected by arrows. The first oval is labeled ‘x’ and connects to the second oval labeled ‘g(x)’ by an arrow labeled ‘g’. The second oval connects to the third oval labeled ‘f(g(x))’ by an arrow labeled ‘f’.

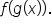
The original input is x, which is then substituted into g open parentheses x close parentheses. Then, g open parentheses x close parentheses is input into function f, giving the result f open parentheses g open parentheses x close parentheses close parentheses.

The notation used to represent a composition of functions is 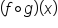open parentheses f ring operator g close parentheses open parentheses x close parentheses, which means 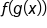f open parentheses g open parentheses x close parentheses close parentheses. The expression 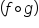open parentheses f ring operator g close parentheses means “f composed with g.”

Using this notation, f is considered the outer function and g is the inner function. Notice that g is used first, then f is applied to the result. Therefore, the outer function is what is applied last. We will see how this works more closely in the next section when we evaluate compositions of functions.

term to know
Composition of Functions
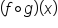Written open parentheses f ring operator g close parentheses open parentheses x close parentheses, it is a function that is obtained by substituting one function into another function.

2. Computing Compositions of Functions

2a. Computing Compositions for Specific Values

EXAMPLE

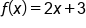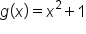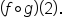
Let f open parentheses x close parentheses equals 2 x plus 3 and g open parentheses x close parentheses equals x squared plus 1. Find and simplify open parentheses f ring operator g close parentheses open parentheses 2 close parentheses.

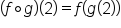
open parentheses f ring operator g close parentheses open parentheses 2 close parentheses equals f open parentheses g open parentheses 2 close parentheses close parentheses Rewrite using the definition of composition.
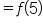
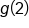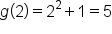
equals f open parentheses 5 close parentheses Since g open parentheses 2 close parentheses is the innermost expression, find that first: g open parentheses 2 close parentheses equals 2 squared plus 1 equals 5
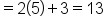
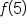equals 2 open parentheses 5 close parentheses plus 3 equals 13 Evaluate f open parentheses 5 close parentheses.

try it
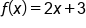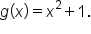
Let f open parentheses x close parentheses equals 2 x plus 3 and g open parentheses x close parentheses equals x squared plus 1.
Find and simplify (g ◦ f )(4).
open parentheses g ring operator f close parentheses open parentheses 4 close parentheses equals g open parentheses f open parentheses 4 close parentheses close parentheses Rewrite using the definition of composition.
equals g open parentheses 11 close parentheses Since f open parentheses 4 close parentheses is the innermost expression, find that first:f open parentheses 4 close parentheses equals 2 open parentheses 4 close parentheses plus 3 equals 11
equals 11 squared plus 1 equals 121 plus 1 equals 122 Evaluate g open parentheses 11 close parentheses.

It is also possible to substitute a function into itself. If you keep the definition in mind, this follows the same format.

EXAMPLE

Let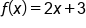 f open parentheses x close parentheses equals 2 x plus 3. Find and simplify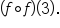 open parentheses f ring operator f close parentheses open parentheses 3 close parentheses.

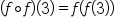
open parentheses f ring operator f close parentheses open parentheses 3 close parentheses equals f open parentheses f open parentheses 3 close parentheses close parentheses Rewrite using the definition of composition.
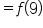
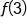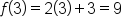
equals f open parentheses 9 close parentheses Since f open parentheses 3 close parentheses is the innermost expression, find that first: f open parentheses 3 close parentheses equals 2 open parentheses 3 close parentheses plus 3 equals 9
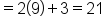
equals 2 open parentheses 9 close parentheses plus 3 equals 21 Evaluate 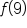f open parentheses 9 close parentheses.

2b. Computing the Expression for a Composition of Functions

The process for finding an expression for a composition is very similar to what we just did in the previous section, but this time there is no value to substitute first.

EXAMPLE

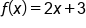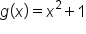Let f open parentheses x close parentheses equals 2 x plus 3 and g open parentheses x close parentheses equals x squared plus 1. Find and simplify open parentheses f ring operator g close parentheses open parentheses x close parentheses.

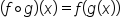
open parentheses f ring operator g close parentheses open parentheses x close parentheses equals f open parentheses g open parentheses x close parentheses close parentheses Rewrite using the definition of composition.
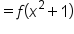
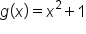equals f open parentheses x squared plus 1 close parentheses Substitute g open parentheses x close parentheses equals x squared plus 1.
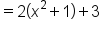equals 2 open parentheses x squared plus 1 close parentheses plus 3
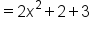equals 2 x squared plus 2 plus 3
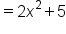
equals 2 x squared plus 5 		Evaluate the function and simplify.

try it
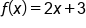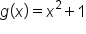Let f open parentheses x close parentheses equals 2 x plus 3 and g open parentheses x close parentheses equals x squared plus 1.
Find and simplify (g ◦ f )(x).
open parentheses g ring operator f close parentheses open parentheses x close parentheses equals g open parentheses f open parentheses x close parentheses close parentheses Rewrite using the definition of composition.
equals g open parentheses 2 x plus 3 close parentheses Substitute f open parentheses x close parentheses equals 2 x plus 3.
equals open parentheses 2 x plus 3 close parentheses squared plus 1
equals open parentheses 2 x plus 3 close parentheses open parentheses 2 x plus 3 close parentheses plus 1
equals 4 x squared plus 12 x plus 9 plus 1
equals 4 x squared plus 12 x plus 10 		Evaluate the function and simplify.

hint
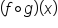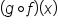Notice that open parentheses f ring operator g close parentheses open parentheses x close parentheses and open parentheses g ring operator f close parentheses open parentheses x close parentheses are not equal. In general, we can assume that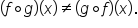 open parentheses f ring operator g close parentheses open parentheses x close parentheses not equal to open parentheses g ring operator f close parentheses open parentheses x close parentheses.

try it
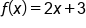Consider the same function as above: f open parentheses x close parentheses equals 2 x plus 3.
Find and simplify (f ◦ f )(x).
open parentheses f ring operator f close parentheses open parentheses x close parentheses equals f open parentheses f open parentheses x close parentheses close parentheses Rewrite using the definition of composition.
equals f open parentheses 2 x plus 3 close parentheses Substitute f open parentheses x close parentheses equals 2 x plus 3.
equals 2 open parentheses 2 x plus 3 close parentheses plus 3
equals 4 x plus 6 plus 3
equals 4 x plus 9 		Evaluate the function and simplify.

There are situations in which a composition can’t be simplified.

EXAMPLE

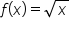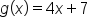If f open parentheses x close parentheses equals square root of x and g open parentheses x close parentheses equals 4 x plus 7, find an expression for open parentheses f ring operator g close parentheses open parentheses x close parentheses.

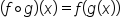
open parentheses f ring operator g close parentheses open parentheses x close parentheses equals f open parentheses g open parentheses x close parentheses close parentheses Rewrite using the definition of composition.
equals f open parentheses 4 x plus 7 close parentheses Substitute 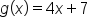g open parentheses x close parentheses equals 4 x plus 7.
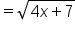
equals square root of 4 x plus 7 end root Evaluate the function.

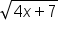There is no algebraic way to simplify square root of 4 x plus 7 end root, so this is the final answer.

EXAMPLE

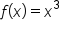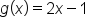If f open parentheses x close parentheses equals x cubed and g open parentheses x close parentheses equals 2 x minus 1, find an expression for open parentheses f ring operator g close parentheses open parentheses x close parentheses.

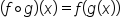
open parentheses f ring operator g close parentheses open parentheses x close parentheses equals f open parentheses g open parentheses x close parentheses close parentheses Rewrite using the definition of composition.
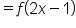
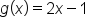equals f open parentheses 2 x minus 1 close parentheses Substitute g open parentheses x close parentheses equals 2 x minus 1.
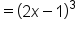
equals open parentheses 2 x minus 1 close parentheses cubed Evaluate the function.

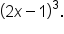
At this point, we could use multiplication to rewrite this expression, but this would be very time-consuming. It is actually more useful to leave the answer as open parentheses 2 x minus 1 close parentheses cubed.

try it
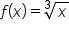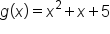Suppose f open parentheses x close parentheses equals cube root of x and g open parentheses x close parentheses equals x squared plus x plus 5.
Find an expression for (f ◦ g )(x).
open parentheses f ring operator g close parentheses open parentheses x close parentheses equals f open parentheses g open parentheses x close parentheses close parentheses Rewrite using the definition of composition.
equals f open parentheses x squared plus x plus 5 close parentheses Substitute g open parentheses x close parentheses equals x squared plus x plus 5.
equals cube root of x squared plus x plus 5 end root Evaluate the function.

3. Decomposing Composite Functions

Given a composition of functions, it is important to be able to identify the inner and outer functions.

For example, each of these functions are compositions of other functions:

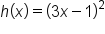
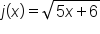
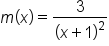
h open parentheses x close parentheses equals open parentheses 3 x minus 1 close parentheses squared j open parentheses x close parentheses equals square root of 5 x plus 6 end root m open parentheses x close parentheses equals 3 over open parentheses x plus 1 close parentheses squared

To decompose composite functions, identify the “inner” function first, then the “outer” function is apparent.

EXAMPLE

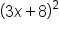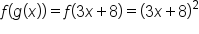Consider the expression open parentheses 3 x plus 8 close parentheses squared, which is the result of a composition of functions. How can we find functions f open parentheses x close parentheses and g open parentheses x close parentheses so that f open parentheses g open parentheses x close parentheses close parentheses equals f open parentheses 3 x plus 8 close parentheses equals open parentheses 3 x plus 8 close parentheses squared?

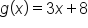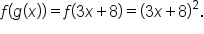
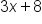To answer this question, start with the expression inside the grouping symbols. Since g open parentheses x close parentheses is the inside function, let g open parentheses x close parentheses equals 3 x plus 8. Then, we have f open parentheses g open parentheses x close parentheses close parentheses equals f open parentheses 3 x plus 8 close parentheses equals open parentheses 3 x plus 8 close parentheses squared.

Now, replace 3 x plus 8 with a symbol, say “?”. We can write 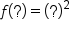f open parentheses ? close parentheses equals open parentheses ? close parentheses squared. As you can see, this tells us that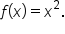 f open parentheses x close parentheses equals x squared.

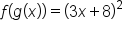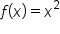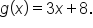
Conclusion: Given f open parentheses g open parentheses x close parentheses close parentheses equals open parentheses 3 x plus 8 close parentheses squared, f open parentheses x close parentheses equals x squared and g open parentheses x close parentheses equals 3 x plus 8.

try it
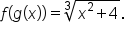
Suppose f open parentheses g open parentheses x close parentheses close parentheses equals cube root of x squared plus 4 end root.
Find functions f (x) and g (x) to make the above composition of functions true.
The inside function is g open parentheses x close parentheses equals x squared plus 4 and the outside function is f open parentheses x close parentheses equals cube root of x.

4. Applications of Compositions

When a stone is dropped into a lake, a circular ripple forms and continues to get larger until it dissipates. After t seconds, the radius (in inches) of the ripple is 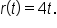r open parentheses t close parentheses equals 4 t. Recall also that the area of a circle with radius r is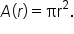 A open parentheses r close parentheses equals πr squared.

EXAMPLE

Suppose we want to find a function for the area inside the ripple, but as a function of time, t. Here is how the functions work together: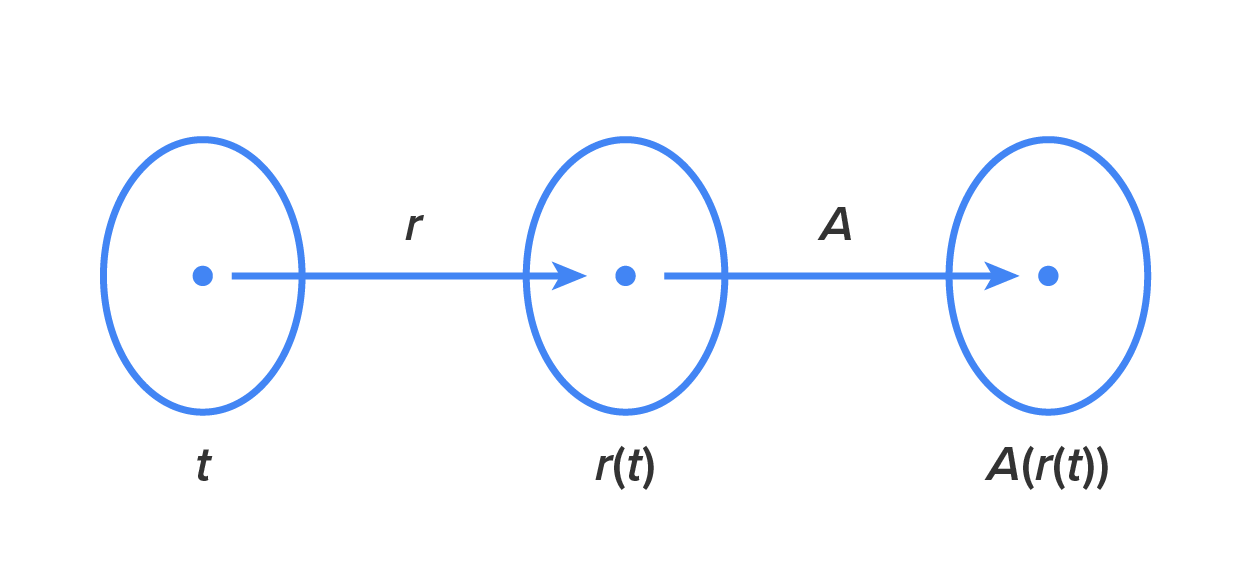

A mathematical composition represented by three ovals connected by arrows. The first oval is labeled ‘t’ and connects to the second oval labeled ‘r(t)’ by an arrow labeled ‘r’. The second oval connects to the third oval labeled ‘A(r(t))’ by an arrow labeled ‘A’.

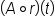Therefore, the composition open parentheses A ring operator r close parentheses open parentheses t close parentheses will give the area enclosed by the ripple after t seconds.

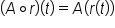
open parentheses A ring operator r close parentheses open parentheses t close parentheses equals A open parentheses r open parentheses t close parentheses close parentheses Use the definition of composition.
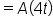
equals A open parentheses 4 t close parentheses Replace 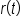r open parentheses t close parentheses with 4t.
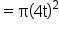
equals straight pi open parentheses 4 straight t close parentheses squared Evaluate the function.
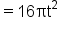
equals 16 πt squared Simplify.

Notice that A is the outer function, which means that the result is an area. Notice also that using this function allows us to bypass knowing the radius in order to get the area.

EXAMPLE

The radius of a circle is given by the function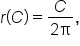 r open parentheses C close parentheses equals fraction numerator C over denominator 2 straight pi end fraction comma where C is the circumference of the circle. Recall also that the area of a circle is 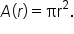A open parentheses r close parentheses equals πr squared. Using this information, we can find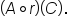 open parentheses A ring operator r close parentheses open parentheses C close parentheses.

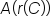
A open parentheses r open parentheses C close parentheses close parentheses Rewrite using the definition.
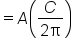
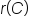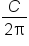equals A open parentheses fraction numerator C over denominator 2 straight pi end fraction close parentheses Replace r open parentheses C close parentheses with fraction numerator C over denominator 2 straight pi end fraction.
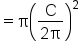
equals straight pi open parentheses fraction numerator straight C over denominator 2 straight pi end fraction close parentheses squared Evaluate the function.
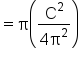
equals straight pi open parentheses fraction numerator straight C squared over denominator 4 straight pi squared end fraction close parentheses Apply the exponent.
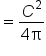
equals fraction numerator C squared over denominator 4 straight pi end fraction Remove the common factor of straight pi.

This function gives the area of a circle when its circumference is known. This could be very useful since it is easier to measure the circumference of a circle than it is its radius.

summary
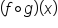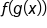In this lesson, you learned the definition of a composition of functions, which is a function that is obtained by substituting one function into another function. Written open parentheses f ring operator g close parentheses open parentheses x close parentheses, or f open parentheses g open parentheses x close parentheses close parentheses, it means to substitute g open parentheses x close parentheses into f open parentheses x close parentheses. You learned how to compute compositions of functions, including both computing compositions for specific values and computing the expression for a composition of functions. You learned how to decompose composite functions by identifying the “inner” function first, after which the “outer” function is apparent. Finally, you explored applications of compositions in real-world situations.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Composition of Functions

Written open parentheses f ring operator g close parentheses open parentheses x close parentheses, it is a function that is obtained by substituting one function into another function.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.