Table of Contents |
Since 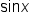 and
and 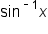 are inverses of each other, it stands to reason that
are inverses of each other, it stands to reason that 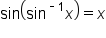 and
and 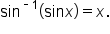 Since
Since 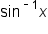 has a restricted domain and range, this is not true for all real numbers x.
has a restricted domain and range, this is not true for all real numbers x.
Consider the expression 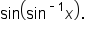
Since the domain of 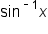 is
is 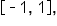
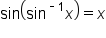 when
when 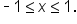
Now consider the expression 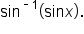
Since the restricted domain 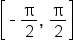 is considered for
is considered for 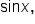
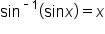 when
when 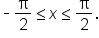
EXAMPLE
Consider the expression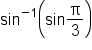 . Since
. Since 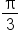 is in the interval
is in the interval 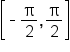 , it follows that
, it follows that  .
.
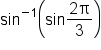 . Since
. Since 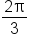 is not in the interval
is not in the interval 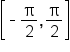 , it follows that
, it follows that 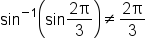 . We will explore how to evaluate expressions like this later.
. We will explore how to evaluate expressions like this later.
The table below summarizes the inverse properties for the trigonometric functions.
| Inverse Property | Domain |
|---|---|
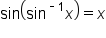
|
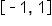
|
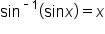
|
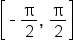
|
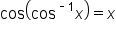
|
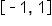
|
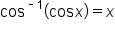
|
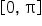
|
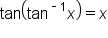
|
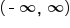
|
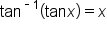
|
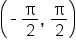
|
EXAMPLE
Consider the expressions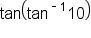 and
and 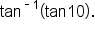
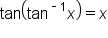 for all real numbers,
for all real numbers, 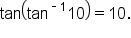
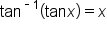 only in the domain
only in the domain 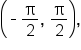 the value of
the value of 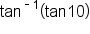 is not 10.
is not 10.
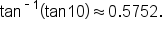
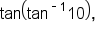 the answer is 10.
the answer is 10.
EXAMPLE
Consider the expressions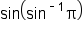 and
and 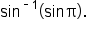
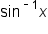 is defined only on the interval
is defined only on the interval 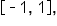
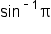 is undefined since
is undefined since 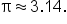

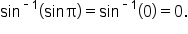
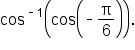
Now we’ll evaluate expressions such as 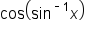 and
and 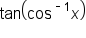 , where the inverse trigonometric function and the trigonometric function are not inverses.
, where the inverse trigonometric function and the trigonometric function are not inverses.
EXAMPLE
Find the exact value of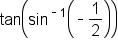 without using a calculator.
without using a calculator.
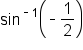 is the angle
is the angle  such that
such that 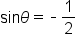 and
and 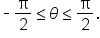
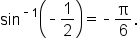
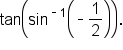
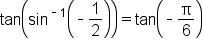
|
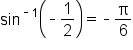
|
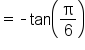
|
Use an even/odd identity. |
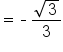
|
This is the tangent function of a special angle. |
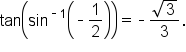
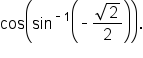
When the trigonometric values are not from special angles, it is not efficient to find the angle first as we did with special angles. Either identities or right triangles need to be used.
EXAMPLE
Evaluate the expression
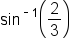 represents an angle. Let
represents an angle. Let 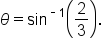 Then,
Then, 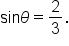
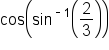 becomes
becomes  when
when 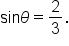
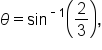 we know that
we know that  terminates in quadrant I since the argument is positive.
terminates in quadrant I since the argument is positive.
 is in quadrant I, we also know that
is in quadrant I, we also know that 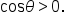
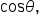 we can use identities as we have in the past, or we can use a right triangle argument.
we can use identities as we have in the past, or we can use a right triangle argument.
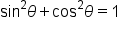
|
This Pythagorean identity relates 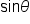 and and 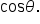
|
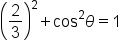
|
Substitute 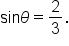
|
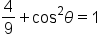
|
Simplify. |
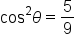
|
Subtract 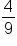 from both sides to isolate from both sides to isolate 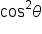 on one side. on one side.
|
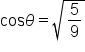
|
Apply the square root principle. Since 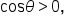 only the positive solution is considered. only the positive solution is considered.
|
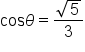
|
Simplify the radical. |
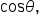 it follows that
it follows that 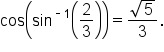
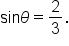
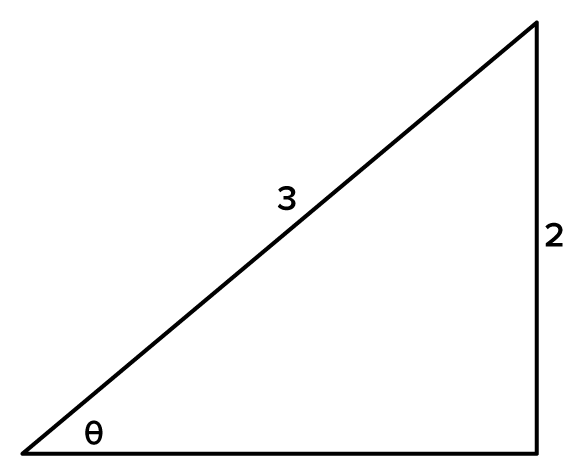
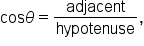 find the length of the adjacent side. Let
find the length of the adjacent side. Let 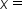 the adjacent side.
the adjacent side.

|
This is the Pythagorean theorem. |
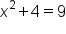
|
Simplify. |

|
Subtract 4 from both sides to isolate 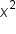 on one side. on one side.
|
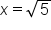
|
Apply the square root principle. Since x is the length of a side, only the positive solution is considered. |
 as found using the other method.
as found using the other method.
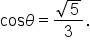
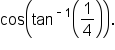
EXAMPLE
Evaluate the expression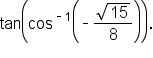
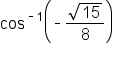 represents an angle. Let
represents an angle. Let 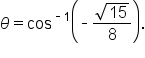 Then,
Then, 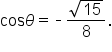
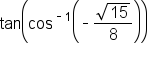 becomes
becomes 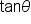 when
when 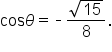
 we know that
we know that  terminates in quadrant II since the argument is negative and the range of the inverse cosine function is
terminates in quadrant II since the argument is negative and the range of the inverse cosine function is 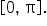
 is in quadrant II, we also know that
is in quadrant II, we also know that 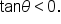
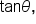 remember that
remember that 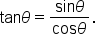 This means we can use the identity
This means we can use the identity 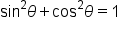 to find
to find 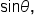 which in turn can be used to find
which in turn can be used to find 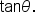
 terminates in quadrant II,
terminates in quadrant II, 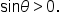
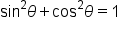
|
This Pythagorean identity relates 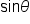 and and 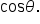 The value of The value of 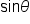 will be used to find the value of will be used to find the value of 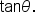
|
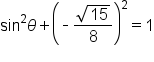
|
Substitute 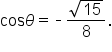
|
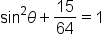
|
Simplify. |
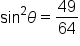
|
Subtract 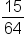 from both sides to isolate from both sides to isolate 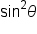 on one side. on one side.
|
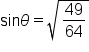
|
Apply the square root principle. Since 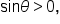 only the positive solution is considered. only the positive solution is considered.
|
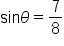
|
Simplify the radical. |
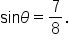
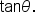
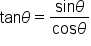
|
This is the quotient identity. |
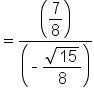
|
Replace 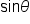 and and  with their values. with their values.
|
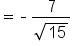
|
Simplify. |
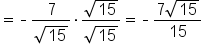
|
Rationalize the denominator. |
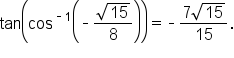
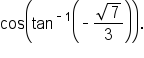
It is also possible to apply these methods to expressions with variables in them. This is an important skill in calculus.
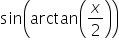 as an algebraic function of x.
as an algebraic function of x.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.