Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Comparing Limits of Functions: Squeeze Theorem

Author: Sophia
PDF Version

what's covered
In this lesson, you will evaluate more difficult limits by comparing them to other known limits. Specifically, this lesson will cover:

Table of Contents

1. Defining the Squeeze Theorem

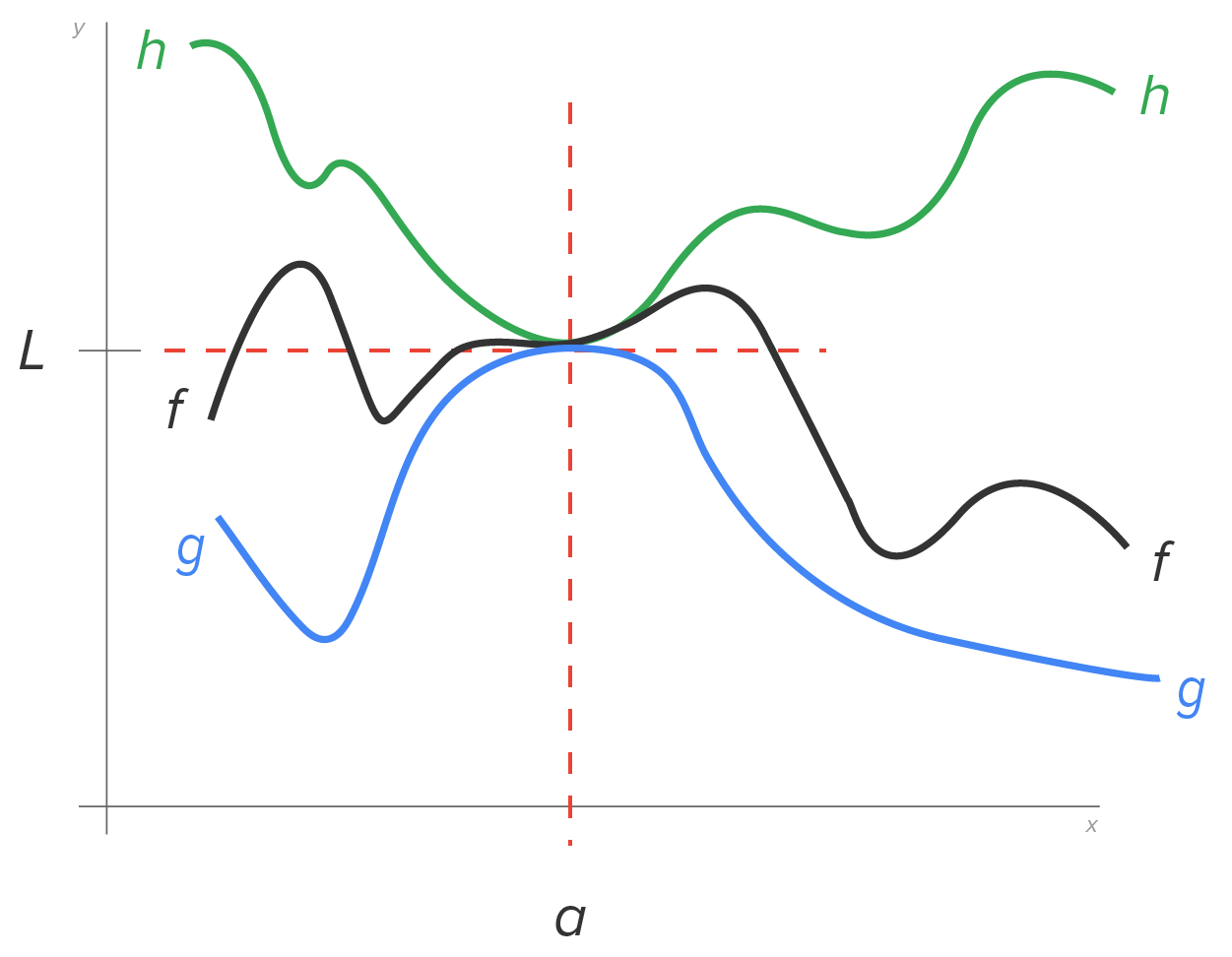
The squeeze theorem is a theorem that uses limit values and states the following:

key concept
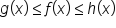Suppose that g open parentheses x close parentheses less or equal than f open parentheses x close parentheses less or equal than h open parentheses x close parentheses for all values of x near 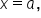x equals a comma as shown in the figure below.

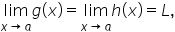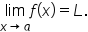
If limit as x rightwards arrow a of g open parentheses x close parentheses equals limit as x rightwards arrow a of h open parentheses x close parentheses equals L comma then limit as x rightwards arrow a of f open parentheses x close parentheses equals L.

A graph with an x-axis and a y-axis. The x-axis has a value labeled ‘a’, and the y-axis has a value labeled ‘L’. A vertical dashed line at x equals a and a horizontal dashed line at y equals L intersect, representing (a, L) as the point of intersection. Three curves labeled ‘h’, ‘f’, and ‘g’ all pass through this point. The curve ‘h’ is positioned above the horizontal dashed line at y equals L. It starts from the upper left corner, rises gently, dips, rises again, and then dips to reach the point (a, L). After crossing the point (a, L), the curve rises, dips again, and then rises again. The curve ‘f’ oscillates around the horizontal dashed line. It starts below the line, rises to a gentle peak above the line, and then dips before rising to meet the point (a, L). After passing through this point, it rises slightly, falls sharply below the line, and then rises again slightly. The curve ‘g’ starts below the horizontal dashed line, descends to an inverted peak, and rises to meet the point (a, L). After passing through this point, it continues briefly before descending sharply below y equals L.

2. Evaluating Limits by Using the Squeeze Theorem

You can evaluate limits by using the squeeze theorem.

EXAMPLE

Consider the limit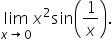 limit as x rightwards arrow 0 of x squared sin open parentheses 1 over x close parentheses. Note that direct substitution does not work since the function is undefined when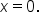 x equals 0.

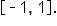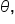
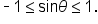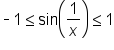
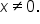
Recall that the range of the sine function is open square brackets short dash 1 comma space 1 close square brackets. This means for any choice of angle theta comma short dash 1 less or equal than sin theta less or equal than 1. This also means that short dash 1 less or equal than sin open parentheses 1 over x close parentheses less or equal than 1 x not equal to 0.

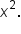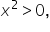Now, multiply all three parts of the inequality by x squared. Since x squared greater than 0 comma the direction of the inequalities is preserved:

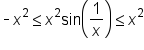
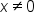
short dash x squared less or equal than x squared sin open parentheses 1 over x close parentheses less or equal than x squared x not equal to 0

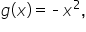
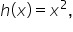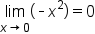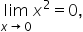Let g open parentheses x close parentheses equals short dash x squared comma h open parentheses x close parentheses equals x squared comma and f open parentheses x close parentheses equals x squared sin open parentheses 1 over x close parentheses. Since limit as x rightwards arrow 0 of open parentheses short dash x squared close parentheses equals 0 and limit as x rightwards arrow 0 of x squared equals 0 comma it follows by the squeeze theorem that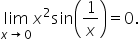 limit as x rightwards arrow 0 of x squared sin open parentheses 1 over x close parentheses equals 0.

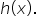
Here is a graph that helps to describe the situation. As you can see, the graph of f open parentheses x close parentheses is always between the graphs of g open parentheses x close parentheses and h open parentheses x close parentheses.

A graph with an x-axis and a y-axis has two dashed curves and a wavy curve. The first dashed curve labeled ‘h(x) equals x squared’ opens upward, starts above the x-axis in the second quadrant, passes through the origin, and moves into the first quadrant. The second dashed curve labeled ‘g(x) equals –x squared’ opens downward, starts below the x-axis in the third quadrant, passes through the origin, and then moves into the fourth quadrant. The wavy curve labeled ‘f(x) equals x squared sin 1/x’ oscillates between the two dashed curves, exhibiting sinusoidal behavior as it moves outward from the origin along the x-axis.

EXAMPLE

Suppose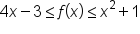 4 x minus 3 less or equal than f open parentheses x close parentheses less or equal than x squared plus 1 for all x near 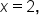x equals 2 comma except possibly at 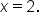x equals 2. Let's evaluate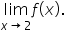 limit as x rightwards arrow 2 of f open parentheses x close parentheses.

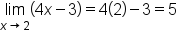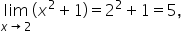Since limit as x rightwards arrow 2 of open parentheses 4 x minus 3 close parentheses equals 4 open parentheses 2 close parentheses minus 3 equals 5 and limit as x rightwards arrow 2 of open parentheses x squared plus 1 close parentheses equals 2 squared plus 1 equals 5 comma it follows by the squeeze theorem that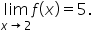 limit as x rightwards arrow 2 of f open parentheses x close parentheses equals 5.

try it
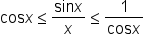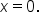Consider the fact that cos x less or equal than fraction numerator sin x over denominator x end fraction less or equal than fraction numerator 1 over denominator cos x end fraction near x equals 0. Suppose you want to find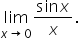 limit as x rightwards arrow 0 of fraction numerator sin x over denominator x end fraction.
Evaluate this limit.
Note that limit as x rightwards arrow 0 of cos x equals 1 and limit as x rightwards arrow 0 of fraction numerator 1 over denominator cos x end fraction equals 1.

Since cos x less or equal than fraction numerator sin x over denominator x end fraction less or equal than fraction numerator 1 over denominator cos x end fraction comma it follows that limit as x rightwards arrow 0 of fraction numerator sin x over denominator x end fraction equals 1.

summary
In this lesson, you learned the definition of the squeeze theorem, which lets us find the limit of a function as x approaches a whose function values are between two other functions on both sides of a, and where the limits of the two other functions are the same as x approaches a. You learned that you can use the squeeze theorem to evaluate limits that are particularly difficult, with functions that have function values between two functions with known and equal limit values.

Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 1 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.