Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Characteristics of Graphs of Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will use the graph of a function to determine how it changes. Specifically, this lesson will cover:

Table of Contents

1. Using a Graph to Determine Where a Function Is Increasing, Decreasing, or Constant

When we take a graph and examine it over an interval of x-values, we can observe many things.

Here are a few questions we could ask:

  • Is the graph rising, falling, or flat?
  • Does the graph have any high points?
  • Does the graph have any low points?
  • How do the high and low points relate to where the graph is rising or falling?
In this tutorial, we will answer all these questions.

There are three key properties of functions in terms of how they change: increasing, decreasing, and constant. Imagine you are traversing a graph from left to right.

big idea
A function is increasing on an interval of x-values if its y-values increase (the graph rises) as the x-values increase.

A function is decreasing on an interval of x-values if its y-values decrease (the graph falls) as the x-values increase.

A function is constant on an interval of x-values if its y-values do not change (flat, horizontal) as the x-values increase.

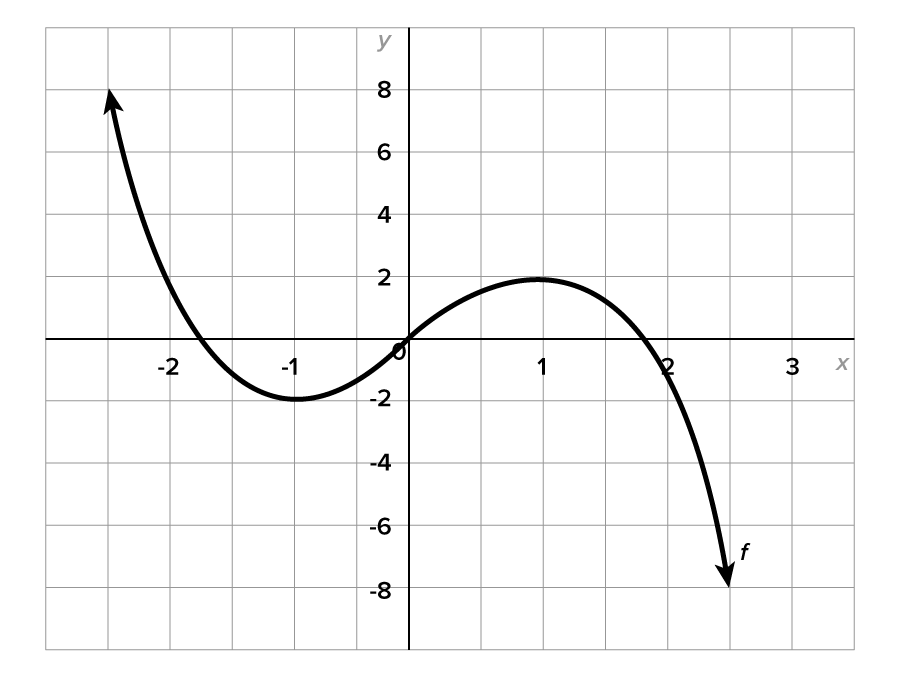
To see how this works, consider the graph of 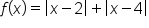f open parentheses x close parentheses equals open vertical bar x minus 2 close vertical bar plus open vertical bar x minus 4 close vertical bar shown below.

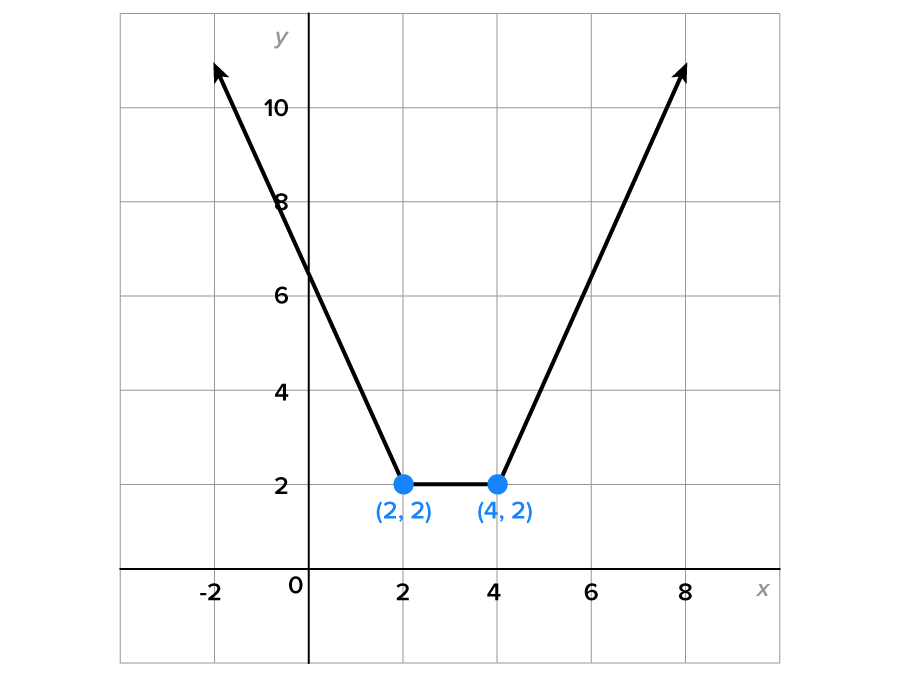
A graph with an x-axis ranging from −2 to 8 and a y-axis ranging from 0 to 10 at intervals of 2. The graph consists of three connected lines. The first line slants downward from the second quadrant, intersecting the y-axis between 6 and 7, then reaches a filled dot at (2, 2). From this point, a second horizontal line segment joins the points (2, 2) and (4, 2), then a third line starts at (4, 2) and slants upward to the right.

As we can see, the graph is falling until the point 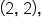open parentheses 2 comma space 2 close parentheses comma then is flat until 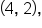open parentheses 4 comma space 2 close parentheses comma then begins to rise.

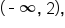More formally, we say that the graph of f open parentheses x close parentheses is decreasing on the interval open parentheses short dash infinity comma space 2 close parentheses comma constant on the interval 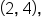open parentheses 2 comma space 4 close parentheses comma and increasing on the interval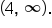 open parentheses 4 comma space infinity close parentheses.

Notice that all these intervals are open. To understand why, consider 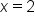x equals 2, for instance. There is no meaningful way to decide whether 2 should be included in the constant interval or the decreasing interval. Therefore, we leave all intervals open.

EXAMPLE

Use the graph below to determine the open intervals over which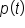 p open parentheses t close parentheses is increasing, decreasing, or constant.

A graph with an x-axis ranging from −1 to 6 and a y-axis ranging from −2 to 4. A curve descends from the second quadrant, crosses the x-axis at (0.4, 0), reaches a rounded minimum around (1, -1), curves upward and crosses through (2, 0), increases until reaching a rounded maximum at (3, 1). The curve then dips downward, reaching a minimum at (4, 0.6), then curves upward rapidly.

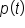Moving from left to right, it appears that p open parentheses t close parentheses is decreasing until the point 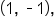open parentheses 1 comma space short dash 1 close parentheses comma then increasing until reaching the point 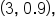open parentheses 3 comma space 0.9 close parentheses comma then decreasing until reaching the point 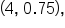open parentheses 4 comma space 0.75 close parentheses comma then increasing indefinitely after that.

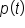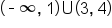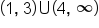Therefore, p open parentheses t close parentheses is decreasing on the intervals open parentheses short dash infinity comma space 1 close parentheses union open parentheses 3 comma space 4 close parentheses and increasing on the intervals open parentheses 1 comma space 3 close parentheses union open parentheses 4 comma space infinity close parentheses.

Now, one for you to try.

try it
Consider this graph:

A graph with an x-axis ranging from −5 to 5 and a y-axis ranging from −60 to 60 at intervals of 20. A curve starts from a point (−5, 5) and rises to a peak at the point (−3, 50). The curve then gradually falls, crossing the point (0, 0). It continues downward, reaching a rounded minimum at the point (3, −50), then curves upward to the point (5, −5). Arrows are drawn at the beginning and end of this graph to indicate that the graph extends past the points (-5, 5) and (5, -5).

Write all open intervals over which the function is increasing, decreasing, or constant.
Increasing on open parentheses short dash infinity comma space short dash 3 close parentheses union open parentheses 3 comma space infinity close parentheses comma decreasing on open parentheses short dash 3 comma space 3 close parentheses.

2. Using a Graph to Locate Local Maxima and Local Minima

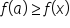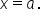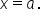A function f open parentheses x close parentheses has a local (or relative) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses for values around x equals a. 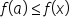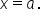A function f open parentheses x close parentheses has a local (or relative) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x close to x equals a. 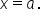In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses for values around x equals a.

hint
To locate local minimum and maximum points on a graph, look for “peaks” and “valleys” on the curve.

EXAMPLE

List all local minimum and maximum points on the following graph.

A graph with an x-axis ranging from −1 to 6 and a y-axis ranging from −2 to 4. A curve descends from the second quadrant, crosses the x-axis at (0.4, 0), reaches a rounded minimum around (1, -1), curves upward and crosses through (2, 0), increases until reaching a rounded maximum at (3, 1). The curve then dips downward, reaching a minimum at (4, 0.6), then curves upward rapidly.
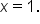
  • open parentheses 1 comma space short dash 1 close parentheses is a local minimum point. This means that the local minimum value is -1 and occurs when x equals 1.
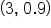  • open parentheses 3 comma space 0.9 close parentheses is a local maximum point. This means that the local maximum value is 0.9 and occurs when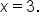 x equals 3.
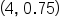  • open parentheses 4 comma space 0.75 close parentheses is a local minimum point. This means that the local minimum value is 0.75 and occurs when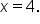 x equals 4.

try it
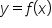Consider the graph of y equals f open parentheses x close parentheses shown below.

A graph with an x-axis ranging from −2 to 3 at intervals of 2 and a y-axis ranging from −8 to 8. The curve descends from the second quadrant, crosses the x-axis at the point (−1.8, 0), reaches a rounded minimum at the point (−1, −2), then ascends into the first quadrant by crossing at the point (0, 0). The curve then reaches a rounded peak at the point (1, 2) and then descends in the fourth quadrant, crossing the x-axis around the point (1.7, 0).

Determine all the local minimum values on the graph.
-2 (occurs at x equals short dash 1).
Determine all the local maximum values on the graph.
2 (occurs at x equals 1).

terms to know
Local (or Relative) Maximum
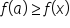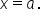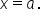
A function f open parentheses x close parentheses has a local (or relative) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses for values around x equals a.
Local (or Relative) Minimum
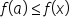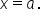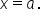
A function f open parentheses x close parentheses has a local (or relative) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses for values around x equals a.

3. Using a Graph to Locate the Absolute Maximum and Absolute Minimum

Absolute minima and maxima are the smallest and largest values of f open parentheses x close parentheses on the entire domain.

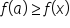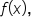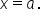A function f open parentheses x close parentheses has a global (or absolute) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x in the domain. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses comma and occurs when x equals a. 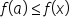A function f open parentheses x close parentheses has a global (or absolute) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x in the domain. 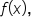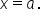In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses comma and occurs when x equals a.

EXAMPLE

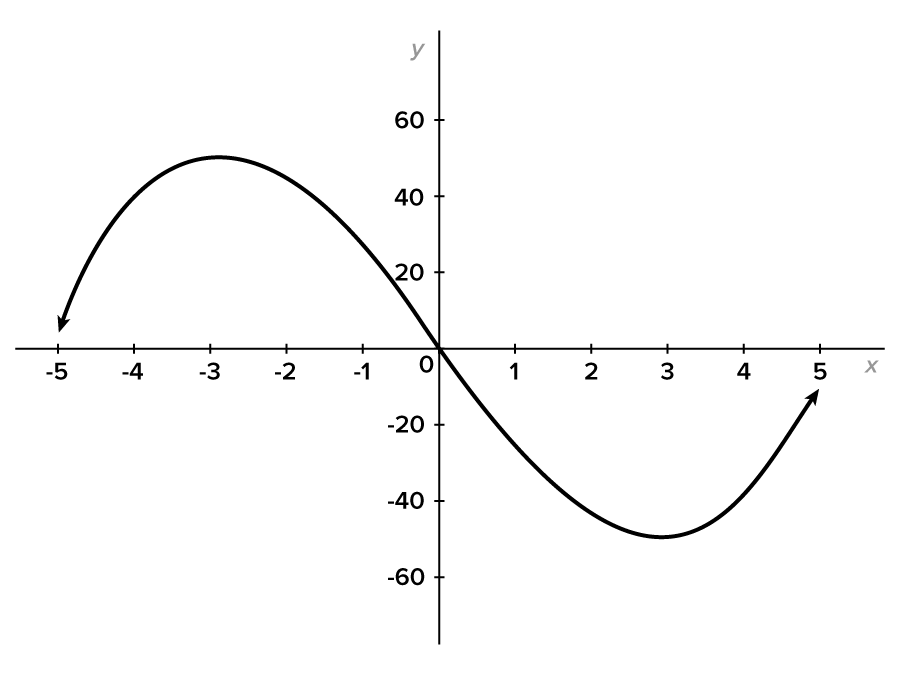
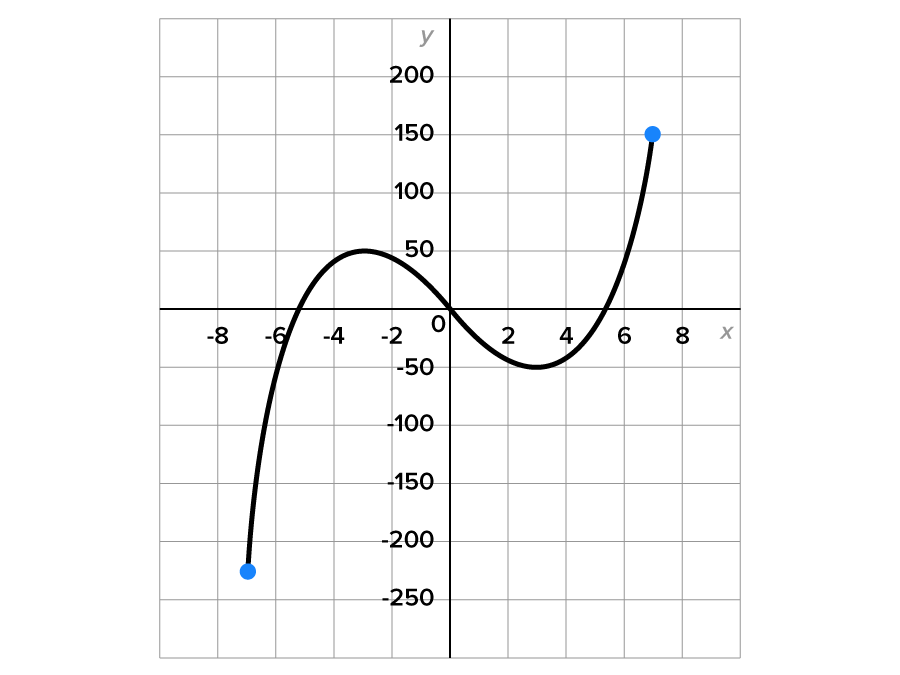
Find all global maximum and minimum values of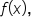 f open parentheses x close parentheses comma where its graph is shown below.

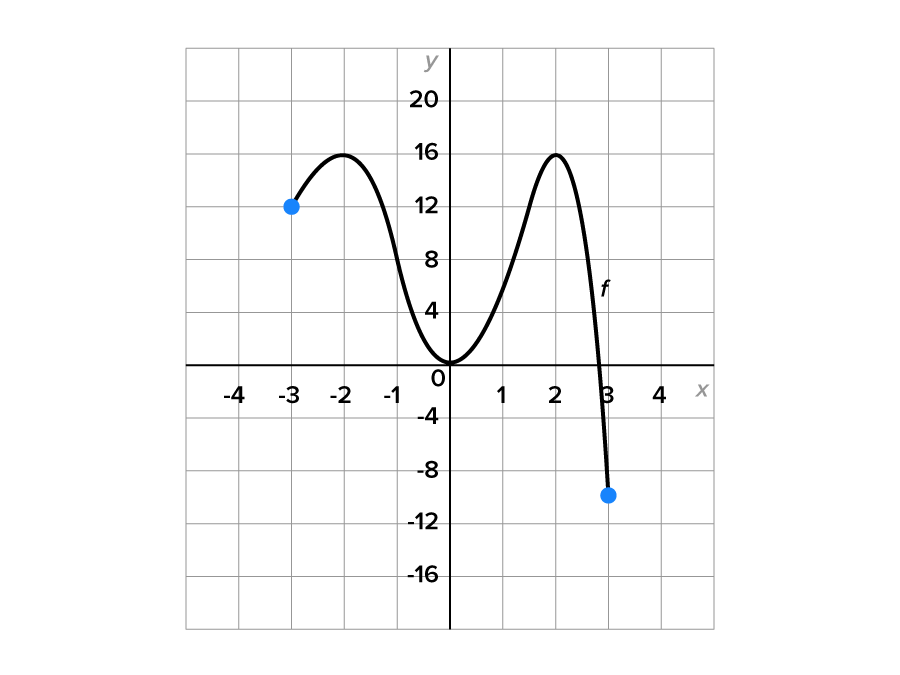
A graph with an x-axis ranging from −4 to 4 and a y-axis ranging from −16 to 20 at intervals of 4. The curve ascends from the filled dot at (−3, 12), reaches a peak at the point (−2, 16), and descends to a rounded minimum at the point (0, 0). From this point, the curve rises steeply until reaching a peak at the point (2, 16). From here, the curve descends into the fourth quadrant and ends at a filled dot at (3, −10).

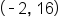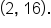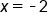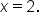
The highest points on the graph are open parentheses short dash 2 comma space 16 close parentheses and open parentheses 2 comma space 16 close parentheses. Therefore, f open parentheses x close parentheses has a global maximum value of 16, which occurs at x equals short dash 2 and x equals 2.

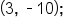The lowest point on the graph is located at open parentheses 3 comma space short dash 10 close parentheses semicolon therefore, the global minimum value is -10 and occurs when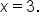 x equals 3.

try it
Consider the graph of y equals f open parentheses x close parentheses shown below.

A graph with an x-axis ranging from −8 to 8 and a y-axis ranging from −250 to 200 at intervals of 50. The curve ascends from the filled dot at (−7, −230), crosses the x-axis at the point (−5, 0), reaches a peak at the point (−3, 50), then descends through the origin into the fourth quadrant, reaching a minimum at the point (3, -50). From here, the graph curves upward, crossing the x-axis at (5, 0), then continues to rise until reaching a filled in circle at (7, 150).

Determine the interval(s) over which f   (x  ) is increasing and decreasing.
Increasing on open parentheses short dash 7 comma space short dash 3 close parentheses union open parentheses 3 comma space 7 close parentheses comma decreasing on open parentheses short dash 3 comma space 3 close parentheses.
Determine all local maximum and minimum values.
Local maximum is 50 at x equals short dash 3 semicolon local minimum is -50 at x equals 3.
Determine all global maximum and minimum values.
Global maximum is about 150 at x equals 7 semicolon global minimum is about -230 at x equals short dash 7.

terms to know
Global (or Absolute) Maximum
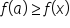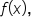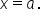
A function f open parentheses x close parentheses has a global (or absolute) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x in the domain. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses comma and occurs when x equals a.
Global (or Absolute) Minimum
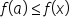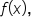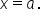
A function f open parentheses x close parentheses has a global (or absolute) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x in the domain. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses comma and occurs when x equals a.

summary
In this lesson, you learned how to use a graph to determine where a function is increasing, decreasing, or constant, by evaluating whether the y-values are increasing (graph rises), decreasing (graph falls), or do not change (graph is flat) on an interval as the x-values increase. You also learned how to use a graph to locate local maxima and local minima, noticing that these are the transition points between increasing and decreasing behavior. 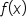Lastly, you learned how to use a graph to locate the absolute maximum and absolute minimum, which are the smallest and largest values of f left parenthesis x right parenthesis on the entire domain. When you get to calculus, you will learn how to find minimum and maximum values by using the function itself rather than relying on graphs.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM 1) CHAPTER 0 AND 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES. 2) OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.

Terms to Know
Global (or Absolute) Maximum

A function f open parentheses x close parentheses has a global (or absolute) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x in the domain. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses comma and occurs when x equals a.

Global (or Absolute) Minimum

A function f open parentheses x close parentheses has a global (or absolute) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x in the domain. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses comma and occurs when x equals a.

Local (or Relative) Maximum

A function f open parentheses x close parentheses has a local (or relative) maximum at x equals a if f open parentheses a close parentheses greater or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the largest value of a function f open parentheses x close parentheses for values around x equals a.

Local (or Relative) Minimum

A function f open parentheses x close parentheses has a local (or relative) minimum at x equals a if f open parentheses a close parentheses less or equal than f open parentheses x close parentheses for all x close to x equals a. In other words, f open parentheses a close parentheses is the smallest value of a function f open parentheses x close parentheses for values around x equals a.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.