Categorical Logic

1. Categorical Logic

Consider the following argument:

1. Some cats are pets.
2. All pets are well cared for.
3. Therefore, some cats are well cared for.

If we were to apply the informal test of validity to this argument, we would see that the argument is valid because it is not possible to imagine a scenario in which the premises are true and yet the conclusion is false. However, look at what happens if we try to translate it using propositional logic. Let’s start with the first sentence.

Some cats are pets.

Translate this as a conditional sentence: “All A are B” would mean “if [a thing is] A, then [a thing is] B.” But even if we create atomic sentences C for “it is a cat,” and P for “it is a pet,” we don’t have a logical connective meaning “sometimes.” A cat chosen at random may or may not be a pet. The best we could do is treat this entire statement as an atomic sentence and assign S as its constant.

For the second statement, we might formulate a sentence, P → W, with P meaning “it is a pet,” and W meaning “it is well cared for,” but we’re back to the same predicament as we were with the first premise when we reach the conclusion, “some cats are well cared for.” The best we can do is use a new variable; S is taken, so we’ll use T.

1. S
2. P → W
3. ∴T

A truth table for this argument will have a row where the premises are true and the conclusion is false, even though the argument is obviously valid. Here is a shortened version:

S	P	W	T	S	P → W	T
T	T	T	F	T	T	F
T	F	T	F	T	T	F
T	F	F	F	T	T	F

We actually couldn’t even derive T in a proof from any of the premises.

This reveals one of the limitations of sentential logic. Some arguments are intuitively valid (such as this one) but cannot be shown to be valid using sentential logic. We need another kind of formal logic to capture a wider range of logically valid inferences.

Categorical logic gives us a formal tool that handles arguments like this. Categorical logic deals with the logical relationships between categorical sentences. A categorical sentence is simply a sentence about sets of things and how they intersect. For example, the first premise of the above argument is a statement about the categories of cats, and the second premise is a statement about the category of pets.

did you know

Categorical logic was developed by the Greek philosopher Aristotle (384-322 BCE). His teachings were gathered by his followers in a text called the Organon around 40 BCE. In Organon, the core notion is of “deduction,” which we now call “syllogism.” Categorical, or Aristotelian, logic is all about deductive reasoning using syllogisms. In this tutorial, we will learn more or less what Aristotle originally proposed in the Organon (though using different terminology and supplemented with Venn diagrams for clarity). Aristotelian logic was the dominant system until the rise of first-order logic in the early 20th century thanks to German mathematician Gottlob Frege (1848-1925 CE).

In contrast with sentential logic, in categorical logic, we use capital letters to stand for parts of sentences that represent categories of things in the world, rather than for whole atomic sentences. For example, we assign C to cats and P to pets, and our first sentence would be:

Some C are P.

It is important to recognize how capital letters are used here as compared to before. In sentential logic, letters stand for whole sentences, things that are declared true, like, “The cat is purring.” In categorical logic, capital letters stand for countable things, either nouns (like “cats”) or noun phrases (like “things that purr”).

try it

Which of the following are categories? Which are sentences?

1. Freshwater fish
2. Fish live in freshwater
3. Mortal humans
4. Humans are mortal
5. German speakers
6. They speak German

Check Your Answers

1, 3, and 5 are categorical terms. 2, 4, and 6 are sentences.

terms to know

Categorical Logic

The branch of logic that deals with logical relationships between categorical sentences.

Categorical Sentence

A sentence about sets of things and how they intersect. They can take four forms: All S are P; No S are P; Some S are P; and Some S are not P.

---

2. Venn Diagrams

In categorical logic, Venn diagrams are used to represent the relationship between categories as potentially overlapping circles.

did you know

You have probably seen “Venn diagrams” in classes, presentations, or even in humorous memes. The diagrams are named for British mathematician and logician John Venn (1834-1923), who did not actually invent the circular diagram (which had been around for centuries). Rather, he further developed Aristotelian logic. The diagrams are used even in non-logic fields.

A Venn diagram is simply a way of graphically representing the logical relationship between two different categories. Below is one that represents the natural language statement, “All humans are mortal,” which involves the categories “humans” and “mortal things.”

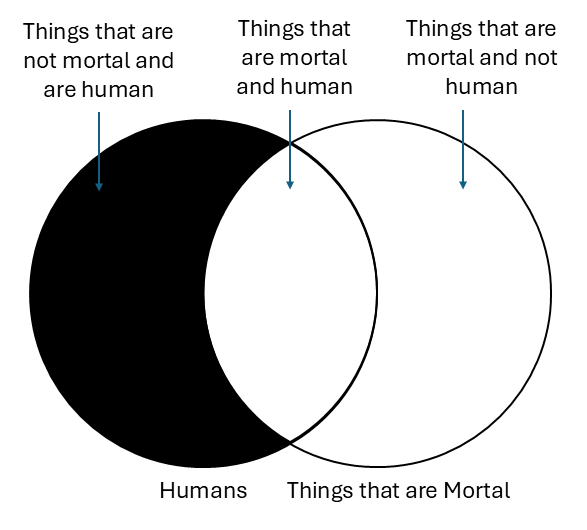
As you see, there are two circles that represent the two categories. They overlap, so their intersection (i.e., the place where the two circles overlap) represents things that are both human and mortal.

hint

Any shaded (blacked out) portions of the Venn diagram represent that there is nothing in that area of the category.

The diagram communicates that there is nothing in the category “humans” that is not also in the category “things that are mortal.” It also shows that there are things that are mortal but that aren’t humans (which is as it should be since, of course, dogs are mortal and yet not human). So, the reason “things that are mortal” is unshaded is because the statement “all humans are mortal” leaves open the possibility that there are things that are not human and yet mortal.

In categorical logic, “All humans are mortal” would be translated as the following categorical sentence:

All H are M.

H represents humans, and M represents mortal things. Remember that we can only work with categories, so a phrase like “is mortal,” or even an abstract uncountable noun like “mortality,” cannot be used. They must first be converted into categories.

This is one of the four categorical sentence forms. We will represent categorical sentences generally using the variables S and P (S stands for subject, which you may remember is the main noun in a statement, and P stands for predicate, the second part of the statement, including the verb, which says something about the subject). Functionally, they are like the propositional variables we used in sentential logic. Only here, they don’t represent whole sentences, but rather parts of the sentence. Below are the four forms and their names with examples.

Sentence Form	Sentence Name	Example
All S are P	Universal Affirmative	All humans are mortal.
No S are P	Universal Negative	No reptiles give live birth.
Some S are P	Particular Affirmative	Some birds are taller than Steph Curry.
Some S are not P	Particular Negative	Some birds don’t fly.

The first two sentence forms, “All S are P” and “No So are P,” are universal; they apply to every possible member of the category S. The next two, “Some S are P” and “Some S are not P,” are particular; they apply to at least one member of that group. We may also use the noun “particular” to refer to a thing that meets that criterion. For example, a particular in the example of the third sentence form is any bird that is taller than Steph Curry, and a particular in the fourth sentence form is any bird that doesn’t fly. In other forms of logic, particulars are sometimes called “existentials,” because you’re looking for at least one thing that exists that satisfies the criteria.

Note that the grammatical form of three of these natural language examples don’t parallel the categorical logic sentences exactly. As with sentential logic, we can translate natural language statements into categorical statements using paraphrases. Once we have categorical paraphrases, we can straightforwardly translate them into categorical sentences. First, we figure out the noun phrase that describes each category that the natural language statement refers to:

• No reptiles are things that give live birth.
• Some birds are things that are taller than Steph Curry.
• Some birds are things that don’t fly.

Although these paraphrases sound strange, using “things are…” confirms that both the subject and the predicate are nouns. Here is a Venn diagram for “No reptiles give live birth.”

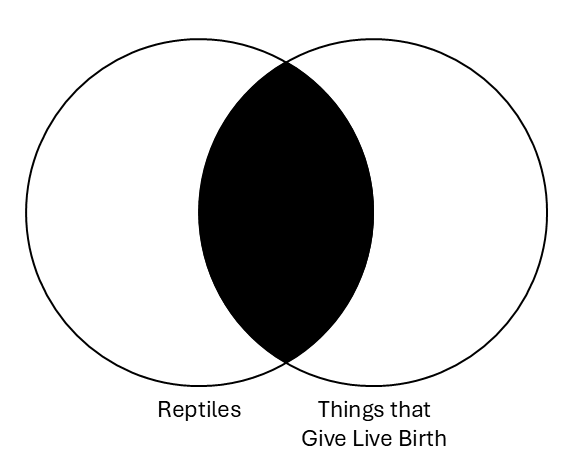
The intersection of “reptiles” and “things that give live birth” is blacked out, showing there is nothing in both categories. This is exactly what our original statement was saying: there isn’t anything that is both a reptile and gives live birth.

Let’s look at the next statement, “Some birds are taller than Steph Curry.” (Steph Curry is, as of 2022, one of the biggest stars in professional basketball.) This is a statement not about all birds, but about some birds. One category is “birds.” The other category is “things that are taller than Steph Curry.” That may sound like a strange category, but it is legitimate. It includes things like adult ostriches, large grizzly bears standing on their hind legs, giraffes, the Flatiron Building, a school bus, etc. Below is the Venn diagram for this statement:

hint

By convention, an asterisk on the Venn diagram means that there is at least one thing in that category.

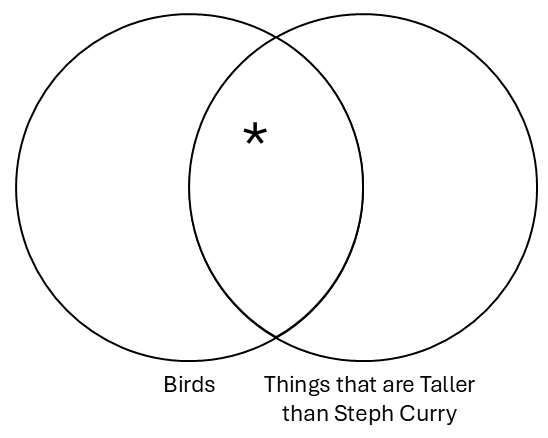
By putting the asterisk in the intersection, we are communicating that there is at least one thing that is a bird and is taller than Steph Curry, which is what our original statement was saying. Ostriches grow to be up to 6’9” tall, and Steph Curry is 6’2” tall.

Finally, consider “Some birds don’t fly.” How would we translate this to the “Some S are not P” form? The first step is to find descriptions of the two categories using either nouns or noun phrases. The “S” term is easy; it is the subject “birds.” But we have to be more careful with the “P” term since the predicate contains a negation. As with atomic sentences, we do not want a category to contain a negation. Instead, we use a negative form, either “No S are P” or “Some S are not P.” We also must make this category a group of countable things. “Flies” is a verb (at least in this context!); adding “things that” before a verb is the magic formula, despite being clunky. This strategy reliably allows us to create a category of countable things from a verb or adjective.

We now have the categorical paraphrase, “Some birds are not things that fly.” Below is the Venn diagram:

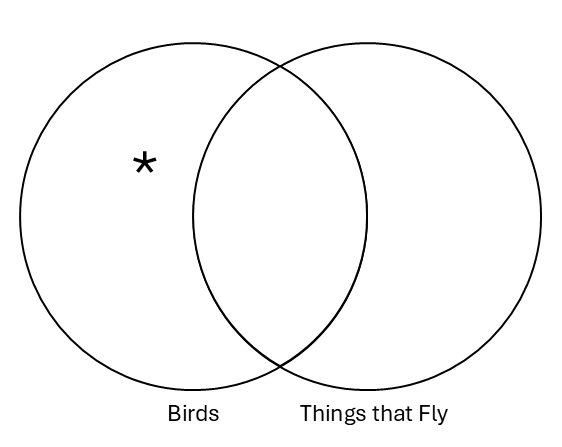
Again, by convention, an asterisk on the Venn diagram means there is at least one thing in that category. By putting the asterisk inside “birds” but outside “things that fly,” we represent that there is at least one thing that is a bird, but that isn’t a flying thing. This is exactly what our original statement was.

Translating categorical statements into their categorical sentences can be tricky. In fact, it is probably one of the trickier things you’ll do in categorical logic. It’s important to check yourself by asking whether your translation accurately captures the meaning of the original statement. Here is a tricky case:

Nobody loves me but my mother.

This is a categorical statement, but which of the four forms does it have? The first step is to determine which categories are referred to. They are: “things that love me” and “things that are my mother.” “My mother” alone, in fact, isn’t a category; it’s a particular. It may sound strange, but remember we are describing categories of things.

The next question is: What is the statement saying about the relationship between the two categories?

hint

The relationship must be one of the four categorical forms (since any categorical statement can be translated into one of the four).

The statement is saying that all the things that love me are my mother. The categorical form is “All S are P.” Thus, the categorical paraphrase would be: “All things that love me are things that are my mother.”

try it

Create a Venn diagram that illustrates the statement, “Nobody loves me but my mother.”

Check Your Answer

This might be unexpected because it implies there are things that are my mother that don’t love me. Why? As you’ll see below, universal statements can be translated into conditionals. So, “All the things that love me are things that are my mother” is identical to “If it’s a thing that loves me, then it is a thing that is my mother.” However, recall that conditionals are true even when their antecedents are false, and their consequents are true. This conditional is true even when a thing doesn’t love me, and that thing is my mother. So, in the diagram, the right-hand side is unshaded to represent this case of vacuous truth.

Here is one final example. Consider this sentence: “The baboon is a fearsome beast.” Which of the four categorical forms would you use?

Although the article “the,” which often denotes particulars, may lead one to think that this is a particular positive form (Some S are P), it is actually a universal positive form (All S are P). This is because the use of “the” in English sometimes denotes a generic subject, not a particular one. A generic subject is a subject that refers to all members of the noun phrase. In this case, “the baboon” means “the species of baboons” or “anything that is baboon” rather than “the one particular baboon I’m talking about.” You may notice a difference in how the words are emphasized when said out loud. More succinctly, the statement means “All baboons are fearsome beasts” rather than “That (particular) baboon is a fearsome beast.” The two categories are: “baboons” and “fearsome beasts.” Since “fearsome beasts” is already a noun phrase, we don’t have to add “things that are…” to it. Using the two category descriptions, the translation into the “All S are P” categorical form is: “All baboons are fearsome beasts.”

try it

Draw a Venn diagram for this sentence, “The baboon is a fearsome beast,” with the generic subject and predicate circles.

Check Your Answer

terms to know

Venn Diagram

A diagram using overlapping circles to represent the relationship between categories.

Subject

The main noun in a sentence/statement.

Predicate

The second half of the sentence, including the verb, which describes the subject.

Universal

In categorical logic, may refer to a categorical sentence about “all” or “none” of the subject category.

Particular

In categorical logic, may refer to a categorical sentence about “some” members of the subject category, or to the members of the group the statement is about.

Generic Subject

A subject that refers to all members of the noun phrase in question.