Table of Contents |
A rational expression is a fraction whose numerator and denominator are polynomials. They are sometimes referred to as algebraic fractions. Reducing rational expressions is similar to reducing numerical fractions. Factors can be canceled only if they appear as factors of both the numerator and the denominator; they are canceled because they reduce to 1.
EXAMPLE
You can see how the fraction below simplifies to 1.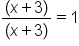
However, terms separated by addition or subtraction in the numerator or denominator cannot be canceled.
EXAMPLE
Consider the expression below.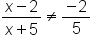

In review, you can simplify fractions by canceling common factors in the numerator and denominator.
EXAMPLE
Suppose you want to simplify the following fraction.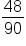

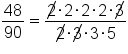
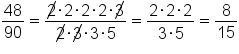
Finding the greatest common factor of a polynomial is a helpful strategy when simplifying algebraic fractions in which common factors appear in both the numerator and denominator.
EXAMPLE
Suppose you want to factor the expression: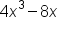
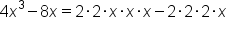
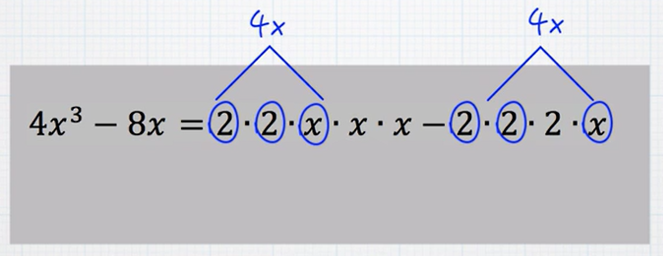
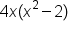
When simplifying rational expressions, you want to start by writing both the numerator and denominator as a products of their prime factors and variable factors.
EXAMPLE
Suppose you want to simplify the following expression.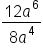
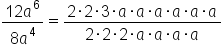
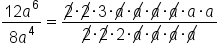
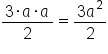
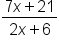
Source: THIS TUTORIAL WAS AUTHORED BY Colleen Atakpu FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.