Calculating Z-Scores

1. Normal Distribution and Z-Scores

Remember from previous lessons that normal distributions have bell-shaped curves.

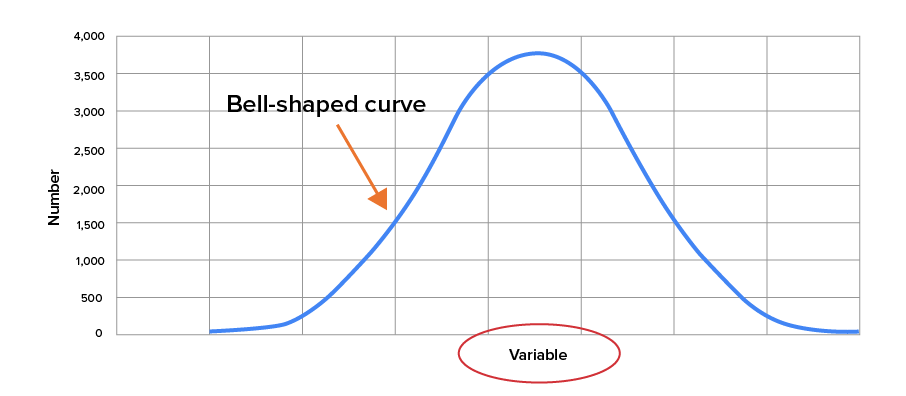
This curve represents the values of a variable and how they are distributed across a range. In a normal distribution, the mean is the center of the distribution. The standard deviation represents how spread out the observations are across the distribution.

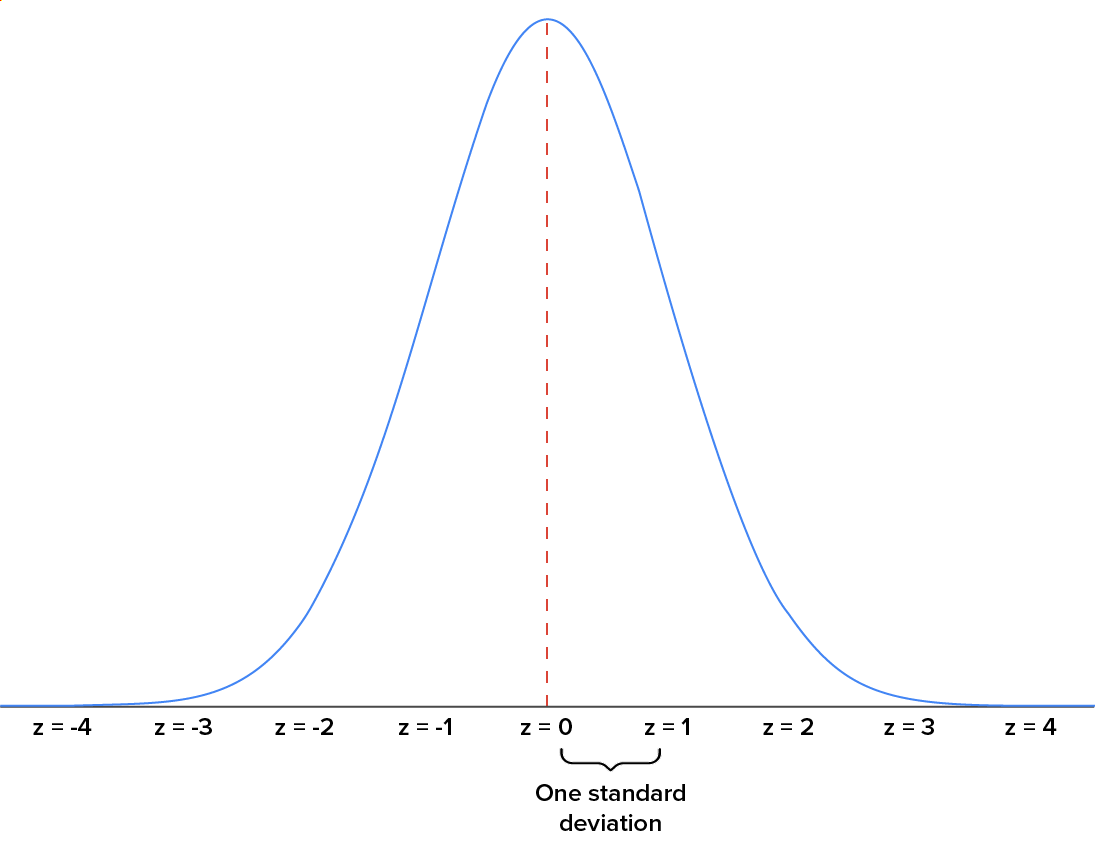
The key reason we use a standard normal distribution is because doing so enables us to easily determine a probability associated with a specific value regarding any normal distribution.

In any standard normal distribution, the mean is always equal to 0, and the standard deviation is always equal to 1. A z-score is what we use to represent the values of the mean and standard deviation when using a standard normal distribution, with a z-score of 0 being equal to the mean and any other value being equivalent to how many standard deviations away from the mean a value lies.

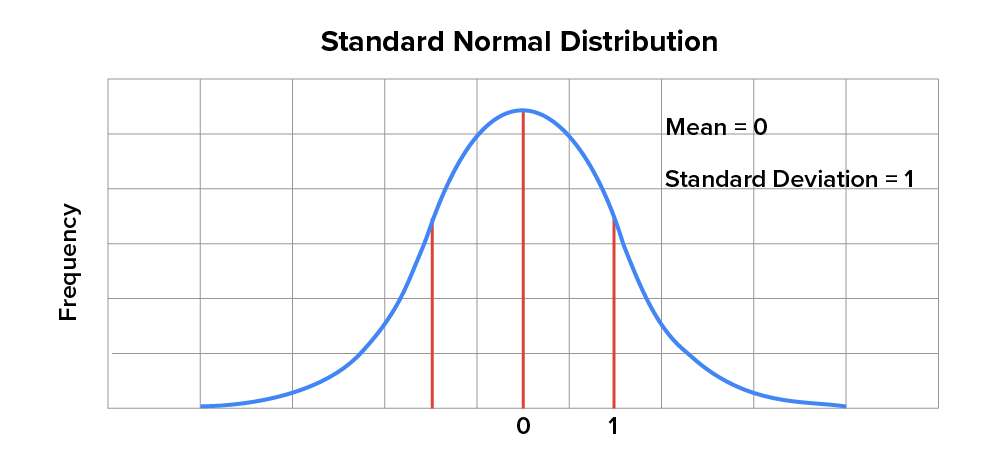
The nice thing about a standard normal distribution is that it can be applied to any normal distribution, so long as you know the mean and standard deviation specific to that distribution. You do this by using the following formula:

formula to know

Z-Score

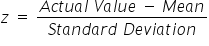
With a normal distribution, as long as you know the mean and the standard deviation, you can determine a z-score. When using the z-score formula, you must subtract the mean from the specific value of interest prior to dividing by the standard deviation.

Remember that population data comes from a larger realm of all values of a specific variable, while sample data comes from a smaller number of observations that are chosen by the researcher. While the mean and the standard deviation can be from either a sample or population when applied to the z-score formula, in this specific instance, we will only look at data that comes from a sample.

IN CONTEXT

There are a variety of different situations in which you might want to convert data into a z-score. One of these could be test scores such as the ACT or the SAT.

Or, suppose you want to measure the size of a particular species specimen. Looking at z-scores would be helpful if you’re interested in whether or not it happens to be a relatively large specimen or a relatively small one.

Looking at economics, you could get a sense of the distribution of household income and the probabilities associated with whether a particular household falls in a relatively high or low range in this regard. By converting values of a variable into z-scores, you are able to make certain that you adhere to a standard process for analyzing data.

term to know

Z-Score

Indicates how many standard deviations away from the mean a value lies.

2. Properties of a Z-Distribution Graph

This graph represents what a z-distribution looks like.

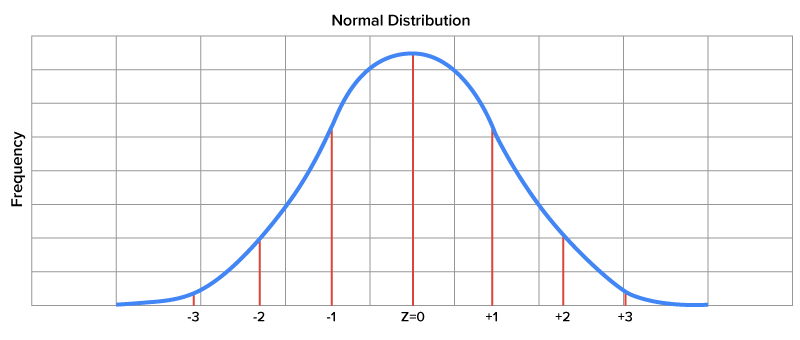
Notice that you have individual numbers that represent how many standard deviations away from the mean a particular point lies. On the horizontal axis, one unit is equal to one standard deviation of the z-distribution.

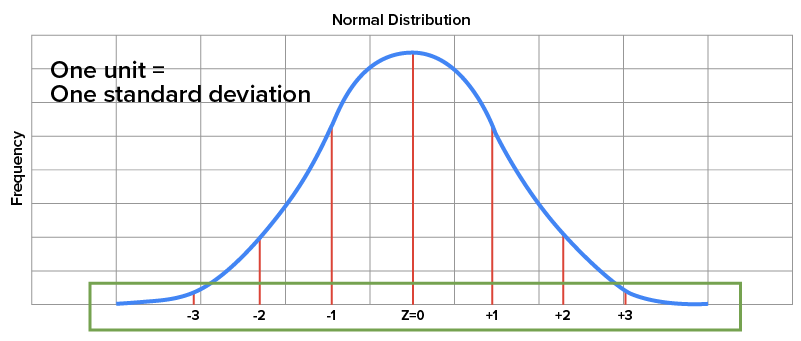
When you look at graphs of a normal distribution, it’s helpful to think of the z-score as illustrating how many standard deviations a value lies above the mean, if the z-score happens to be positive, or below the mean, if the z-score happens to be negative.

3. Calculating a Z-Score

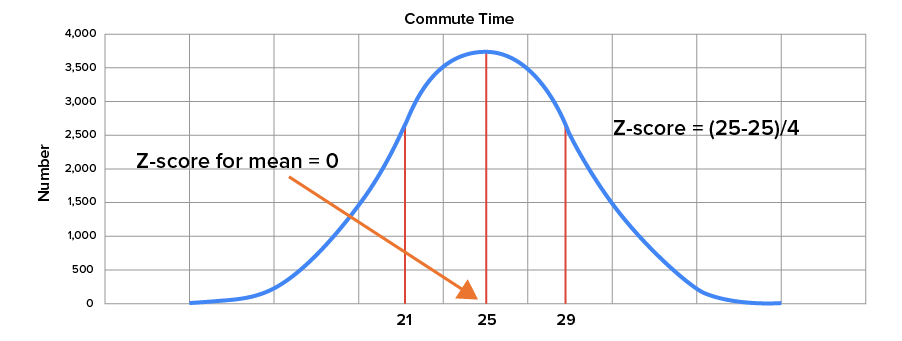
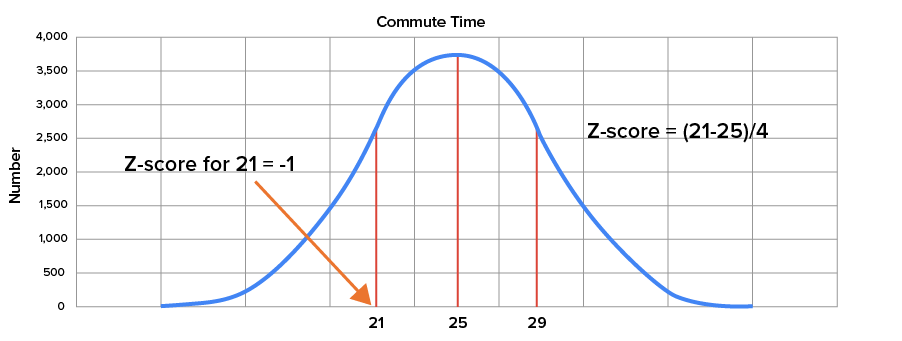
Suppose you were to look at the morning commute times for Americans. They are normally distributed with a mean of 25 minutes and a standard deviation of 4 minutes.

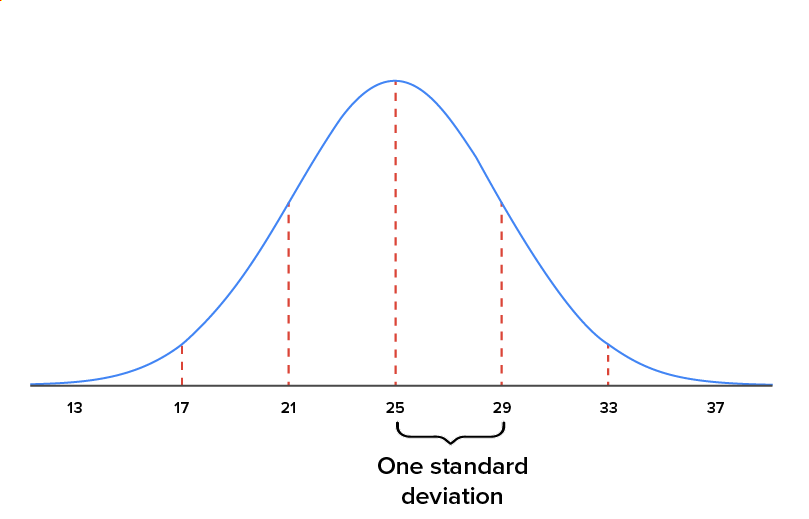
The graphs below illustrate where the mean is located and the points that are one standard deviation to the left and right of the mean.

Value	Z-Score	Graph
25 minutes (mean)	z-score =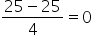
21 minutes	z-score =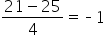
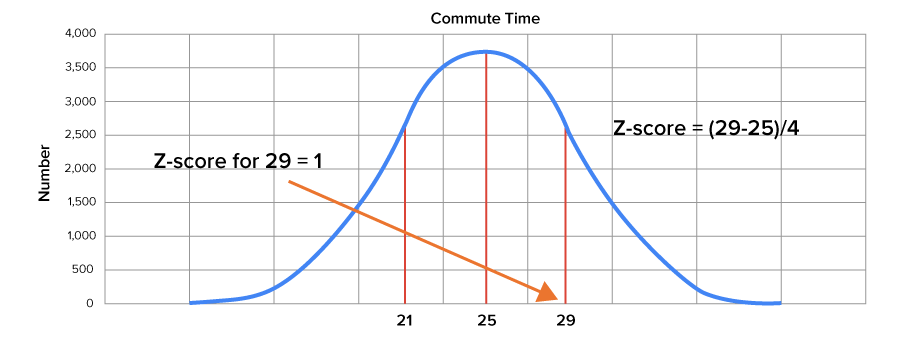
29 minutes	z-score =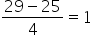

Each of these values would be either one standard deviation to the left of the mean or one standard deviation to the right of the mean. If we add values to the graph corresponding to other quantities of standard deviations away from the mean, we can see the related z-scores.

Value	Z-Score	Graph
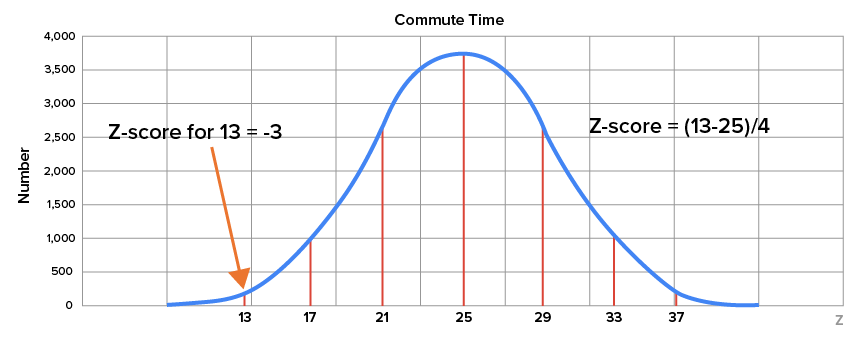
13 minutes	z-score =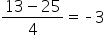
17 minutes	z-score =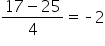
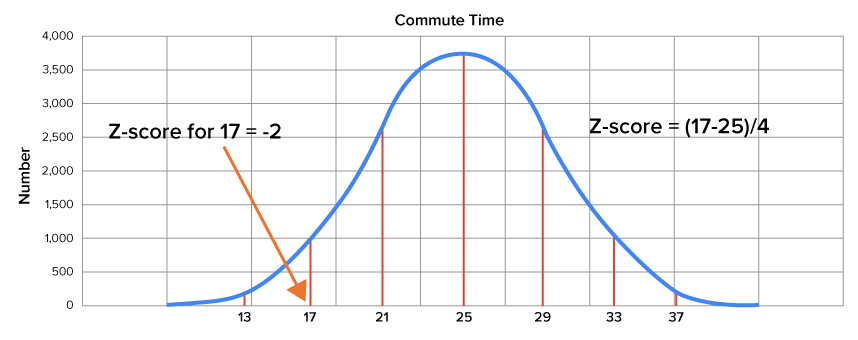
33 minutes	z-score =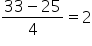
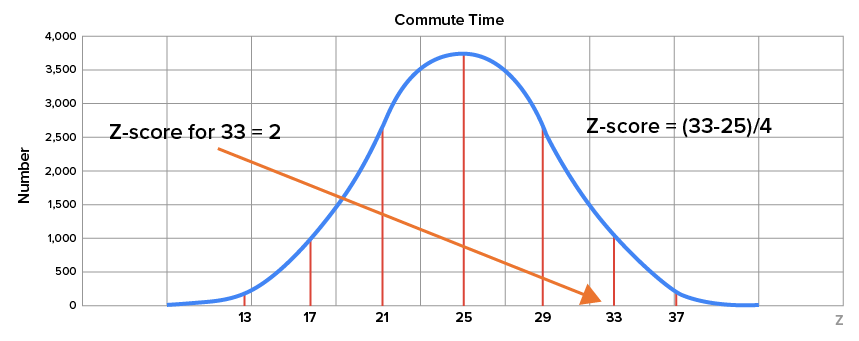
37 minutes	z-score =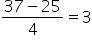

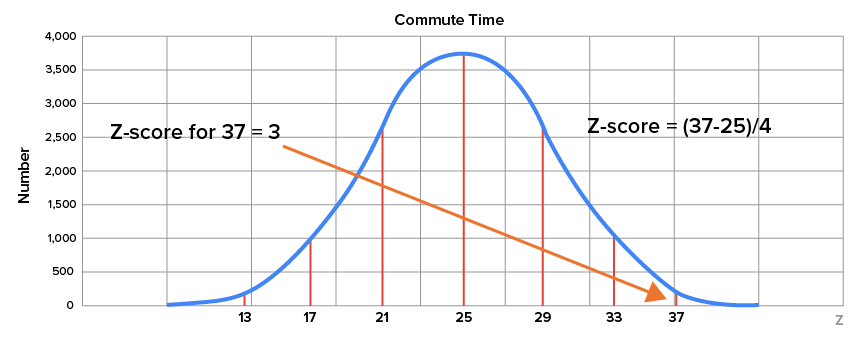
There are often values of a variable that don’t directly correspond to a whole number of standard deviations away from the mean.

try it

Find the following z-scores using the example from above.

What is the z-score for someone with a commute time of 16 minutes?

The z-score would be -2.25.

z-score =

What is the z-score for someone with a commute time of 39 minutes?

The z-score would be 3.5.

z-score =

Knowing a z-score can help you determine how likely it is that an event will occur.