Table of Contents |
A survey is conducted at the local high schools to find out about underage drinking. Of the 523 students who replied to the survey, 188 replied that they have drunk some amount of alcohol.
What is the standard error of the sample proportion?
These students are either answering yes or no on the survey: "Yes, I've drunk some amount of alcohol" or "No, I have not drunk some amount of alcohol." That is qualitative data, also known as categorical data. Therefore, we're dealing with a sample proportion.
Whenever we're dealing with a sample proportion, the next question we need to ask ourselves is, "Do I know the population standard deviation?" In this case, we do not have any of that information. Therefore, the formula to calculate the standard error is p-hat times q-hat, divided by n, all under the square root.

We're actually going to use the data that was given to us, which are estimates—that's what the hat indicates—in order to calculate the standard error.
The first thing we need to do is to figure out what p-hat is, based off of the information given to us. In this case, the p-hat is what we're interested in, and that is how many have answered yes to participating in underage drinking. That would be 188 out of 523 students, or 188/523, which is about 36% of the students.
Now, we also need the complement, which would be q-hat. This is also written as 1 minus p-hat. One minus the 188 out of 523, or 1 - 0.36, tells us that 0.64, or 64%, of the students have not participated in underage drinking. To always make sure our math is correct, remember that our p-hat and q-hat should add up to 1, because they're complements of each other.
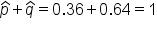
Now, we can plug those values into the formula.
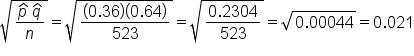
We have 0.36 for p-hat, 0.64 for q-hat, and the total sample, n, was 523 students. This calculates to a standard error that is 0.021.
Revisiting our prior example, a survey is conducted at the local high schools to find out about underage drinking. Of the 523 students who replied to the survey, 188 replied that they have drunk some amount of alcohol. The proportion of underage drinkers nationally is 39%
What is the standard error of the sample proportion?
We are still looking at the students who were surveyed about underage drinking, but notice how this scenario added on that the proportion of underage drinkers nationally is 39%. We're still calculating the standard error of the sample proportion, but in this case, we know the population standard deviation, which is 39%. We're going to use the formula of the square root of pq over n.

We do not need to use p-hat, which is the 188 out of 523, to make the estimate for the standard error. We actually know p, which is 39%, or 0.39.
In this case, we're going to use 0.39 for p. This is another way of indicating population proportion. We can then use this to find q, which is the complement of p. The complement of 0.39 is calculated by 1 minus 0.39, which equals 0.61, or 61%. Sometimes we'll see this written as p subscript 0 and q subscript 0.
The sample size, n, is still 523 students who were surveyed.
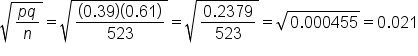
The standard error is 0.021.
Source: THIS TUTORIAL WAS AUTHORED BY RACHEL ORR-DEPNER FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.