Table of Contents |
The standard error for sample means is used when we have quantitative data, and it can be calculated using the following formula:
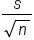
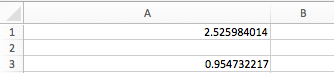
It is the sample standard deviation, s, over the square root of the sample size, n.
EXAMPLE
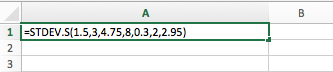
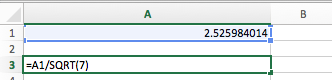
The amount of fallen snow, in inches, is recorded for one week in Minneapolis.| Day | Sunday | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday |
|---|---|---|---|---|---|---|---|
| Snow | 1.5 | 3 | 4.75 | 8 | 0.3 | 2 | 2.95 |



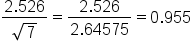

Sample proportions use data that is qualitative, or categorical. When calculating the standard error for sample proportions, you need to consider whether or not you know the population standard deviation. If the population standard deviation is NOT known, you will use the following formula:

The formula to calculate the standard error is p-hat times q-hat, divided by n, all under the square root. We're actually going to use the data that was given to us, which are estimates—that's what the hat indicates.
EXAMPLE
A survey is conducted at the local high schools to find out about underage drinking. Of the 523 students who replied to the survey, 188 replied that they have consumed some amount of alcohol.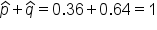
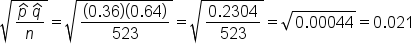
When we have a sample proportion where we do know the population standard deviation, we can use the following formula:

We do not need to use the sample data, p-hat, to make the estimate for the standard error. We actually know the population parameters, so we can use this information.
EXAMPLE
Revisiting our prior example, a survey is conducted at the local high schools to find out about underage drinking. Of the 523 students who replied to the survey, 188 replied that they have consumed some amount of alcohol. The proportion of underage drinkers nationally is 39%.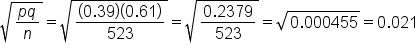
Source: THIS TUTORIAL WAS AUTHORED BY RACHEL ORR-DEPNER FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.