Table of Contents |
Binomial distribution is a probability distribution that follows the binomial setting. A scenario can be considered binomial if it fits these four criteria:
Also, you can rig the scenario to have two outcomes, even if there aren't technically two outcomes. For instance, on a die, there are six outcomes, but perhaps you could call rolling a 5 a success and anything but a 5 a failure. In that case, you've rigged it so that you get two outcomes per trial.
EXAMPLE
 One way to look at this is by following the betting of black on a roulette wheel. Recall that there are 18 black sectors of the total 38 sectors on a roulette wheel.
One way to look at this is by following the betting of black on a roulette wheel. Recall that there are 18 black sectors of the total 38 sectors on a roulette wheel.
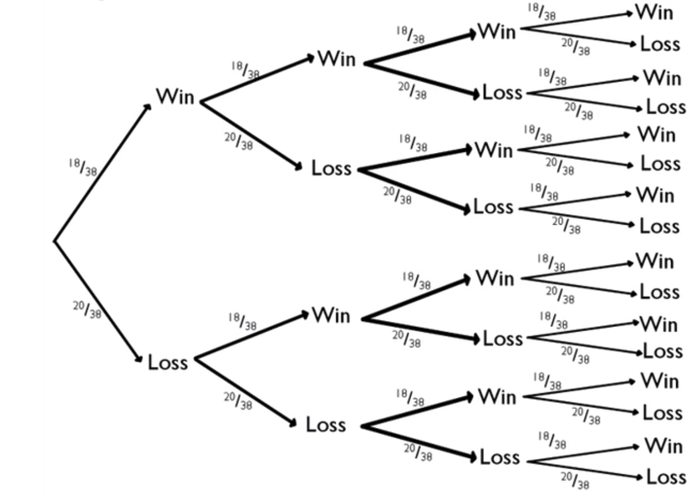
| 0 Wins |
|---|
 1 Outcome |
| 1 Win |
|---|
 4 Outcomes |
| 2 Wins |
|---|
 6 Outcomes |
| 3 Wins |
|---|
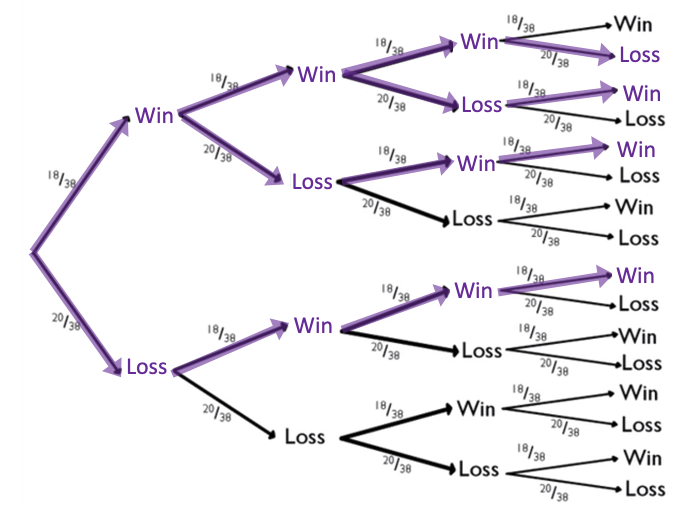 4 Outcomes |
| 4 Wins |
|---|
 1 Outcome |
| Number of Wins | Probability | Explanation |
|---|---|---|
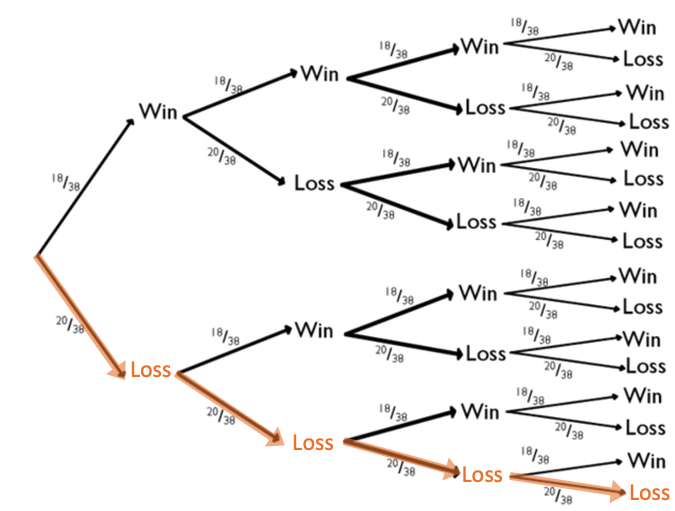
| 0 |
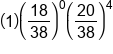
|
Zero wins only happened once. On that branch, 20/38 appeared four times in a row, and 18/38 did not appear at all. |
| 1 |
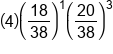
|
One win happened four times. On each of those four branches, 20/38 appeared three times, and 18/38 appeared once. |
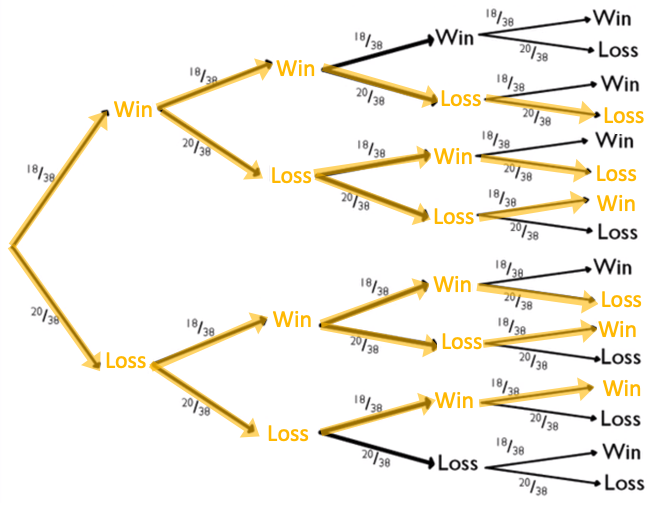
| 2 |
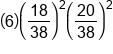
|
Two wins happened six times. On each of those six branches, 20/38 appeared twice, and 18/38 appeared twice. |
| 3 |
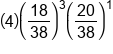
|
Three wins happened four times. On each of those four branches, 18/38 appeared three times, and 20/38 appeared once. |
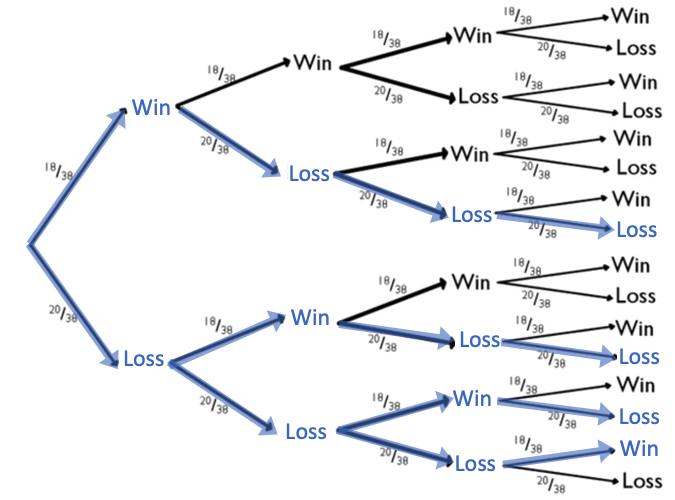
| 4 |
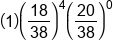
|
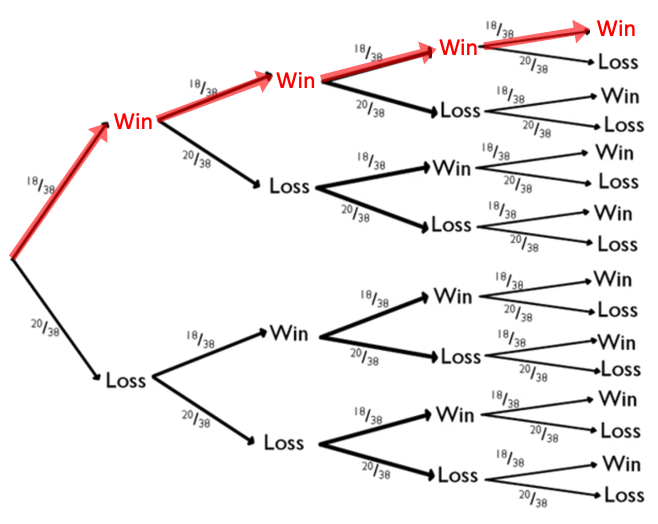
Four wins only happened once. On that branch, 18/38 appeared four times in a row, and 20/38 did not appear at all. |
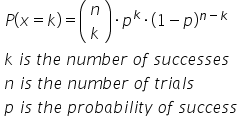
The formula is denoted as: "n, choose k" times the probability of success to the power of k (which means you want to succeed k times out of n times), times the probability of failure (1 minus p) to the power of the rest of the trials that weren't successes, n minus k.
"N, choose k" is sometimes notated subscripted nCk. It's a number of ways to achieve k successes out of n trials. One way to find this amount is by creating a tree diagram and counting up the number of ways. However, if you're using a calculator, most calculators use the command nCr.

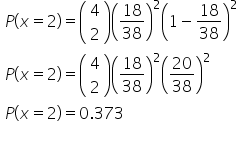
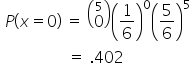
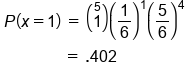
Source: THIS TUTORIAL WAS AUTHORED BY JONATHAN OSTERS FOR SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.