Table of Contents |
Compound interest is like the secret power of a superhero because it gives you powerful growth of your savings over time. Compound interest is when you not only earn interest every year on the original amount you deposit into an account but you also earn interest on interest! Let’s look at an example to see how compound interest and different interest rates, the percentages at which money grows over a specified period, impact your money’s growth over time.
What if you have a choice to put $1,000 into three investment options that earn an annual compound interest rate of 6%, 12%, or 18% at the age of 25? What amount will you have in your account at the end of 40 years when you turn 65 years old with each of these options?
6% over 40 years = $10,286
12% over 40 years = $93,051
18% over 40 years = $750,378
As you can see, the power of compound interest is amazing! We call this the snowball effect, when you earn interest on both your original deposit and interest on the interest.
EXAMPLE
To get another glimpse into the power of compounding, consider an example where you put $1,000 into a savings account that earns 10% annual compound interest. At the end of the year, you earn interest of $100 (i.e., $1,000 × .10). So, at the end of Year 1, you have $1,100 in your account. You then earn an additional $110 in interest by the end of the second year. Now, your account is worth $1,210, and the interest earned in Year 2 is $110. By the end of Year 3, your savings account is worth $1,331. The point is that you not only earn interest every year on the $1,000 you originally deposited but you also earn interest on interest! Moreover, the earlier you start, the more time you have for your interest to snowball.As we can see in the example above, time can make a big difference as to how much money invested today can grow over time. The concept of valuing money at different points in time is called the time value of money, that is, an amount of money is worth more today than the same sum received in the future due to the ability to earn a return from this date forward.
We can use a formula to help us determine the FV when the calculations get more complex with more years. Let’s start with a formula that helps us determine the value of an amount of money at a future date—the FV formula.
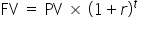
Using the future value (FV) formula above, let’s calculate the FV, or amount grown by an interest rate over time to a later period, of a savings amount using 10% interest as an example. Although interest rates vary given the current economic conditions, we will use 10% since the calculations are simpler.
EXAMPLE
What is the value of an account at the end of 3 years that earns 10% compounded annually on $5,000 deposited today?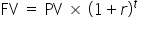
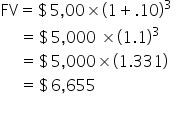
Let’s try some situations that you may want to consider yourself.
EXAMPLE
Take Alex, who is 25 and has saved $3,000. He would like his savings to grow to $5,000 so he can return to community college part-time when his children attend elementary school in 6 years. What will he have in his savings account in 6 years if Alex figures he can earn 8% in a savings account at his local bank?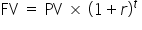
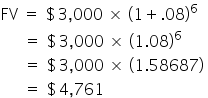
Let’s look at another example and consider the other options you may have when making a financial decision.
EXAMPLE
Let’s say that today is your 20th birthday, and your parents plan to give you $1,000 next year on your 21st birthday. You’d like to buy a used car to drive to make it easier to work at your internship, so you plan on asking for the money now. If you received the $1,000 today, what would it be worth? Another way of saying this is, how much would $1,000 of cash received 1 year from now be worth today?To understand the time value of your deposits or cash flows (cash payments made or received over time), we need to explore the relationships between their values in the future and their equivalent today, or their present value (PV) (the value if money were received today). The PVs today will be less than if we simply added the sum of each future cash deposit in the future to determine their total. Why? Because the cash flows (CFs) are discounted or decreased by the amount of interest growth you could receive if you had all the cash today and invested it.
Understanding this discounted calculation is important to gaining insight into the relationships between time, risk, opportunity cost, and value.
To discount a CF to be received in the future, you need to know:
Regarding the interest rate, you will need to determine your options, the opportunity costs, and the risks of not having the money today.
EXAMPLE
You may be able to put the cash in an account that earns 5% interest or use the cash to pay down a credit card that you are paying 25% on the remaining balance. These two options are examples of your opportunity cost.Obviously, if you receive your $1,000 birthday check today at age 20, you could deposit it into an interest-bearing account. By your 21st birthday, 1 year later, you would have more than $1,000 because you would earn interest on the money over the year. If your bank paid 5% per year on your account balance, then you would earn $50 in interest over the year, or $1,000 × .05 = $50. On your twenty-first birthday, you would have $1,050 in your savings account.
Use this FV formula to calculate the FV of your $1,000 deposited birthday check:
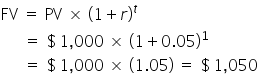
Let’s look at the numbers used in this formula: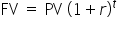 
.
| PV | Interest Rate (r) | Time (t, years) | Future Value |
|---|---|---|---|
| $1,000 | 0.05 | 1 | $1,050 = $1,000 x (1 + 0.05) |
| PV | r | t |
|
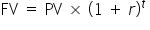
EXAMPLE
If you left the $1,050 in the bank until your 22nd birthday, a year later, you would have this: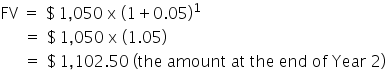
| As t or r increases | the FV of money received in the future increases |
| As t or r decreases | the FV of money received in the future decreases |
We can view your birthday gift another way. What if your parents offered to give you the value of what $1,000 to be received in the future is worth today instead of having to wait 1 year? The value of the $1,000 today is called the discounted value (or PV) and is simply the FV minus the interest you would receive over the next year.
So, let’s look at a formula you can use to determine the PV today of money to be received in the future. Using the same example above of earning 5% interest compounded annually, the rate at which time affects your value is 5% because that’s what having the choice to invest it would earn for you if only you had the $1,000 now. The 5% interest is your opportunity cost. We need to take the FV formula and modify it to get the PV equation.
Use the FV formula:
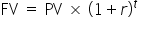
Spin it around.
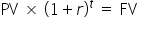
Then, divide each side of the equation by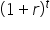 
; we now have our PV formula.
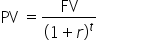
Use the PV formula:
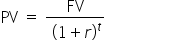
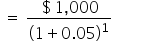
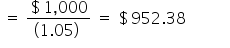
Our answer tells us that your birthday gift would be worth $952.38 if you were to receive its equivalent value today. In other words, if your parents could give you $952.38 on your 20th birthday, you could deposit the money into a savings account earning 5% compound annual interest today, and it would grow to $1,000 1 year from now.
| As t or r increases | the PV of money decreases |
| As t or r decreases | the PV of money increases |
By now, you may be wondering if there is an easy way to figure out how long it takes for your money to double. Yes! Here is one of many golden nuggets you’ll find throughout this course.
It’s called the Rule of 72, which tells you the number of years it takes for your money to double at a given annual rate of return. How? You divide 72 by the return you would receive to find the number of years.
EXAMPLE
If you earn 10%, your money will double in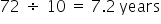
. Or, if you earn 6%, your money will double in 
.
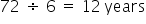Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.
