Table of Contents |
Consider the function 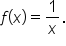 Note that the function is undefined when
Note that the function is undefined when 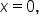 meaning the domain of
meaning the domain of  is
is 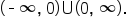 Let’s examine the behavior of
Let’s examine the behavior of  near
near 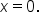
Here is a table of values, which reflects the values of  as x gets closer to 0 on the positive side:
as x gets closer to 0 on the positive side:

|
0.1 | 0.01 | 0.001 | 0.0001 | 0.00001 |
|---|---|---|---|---|---|
|
10 | 100 | 1,000 | 10,000 | 100,000 |
Here is a table of values, which reflects the values of  as x gets closer to 0 from the negative side:
as x gets closer to 0 from the negative side:

|
-0.1 | -0.01 | -0.001 | -0.0001 | -0.00001 |
|---|---|---|---|---|---|
|
-10 | -100 | -1,000 | -10,000 | -100,000 |
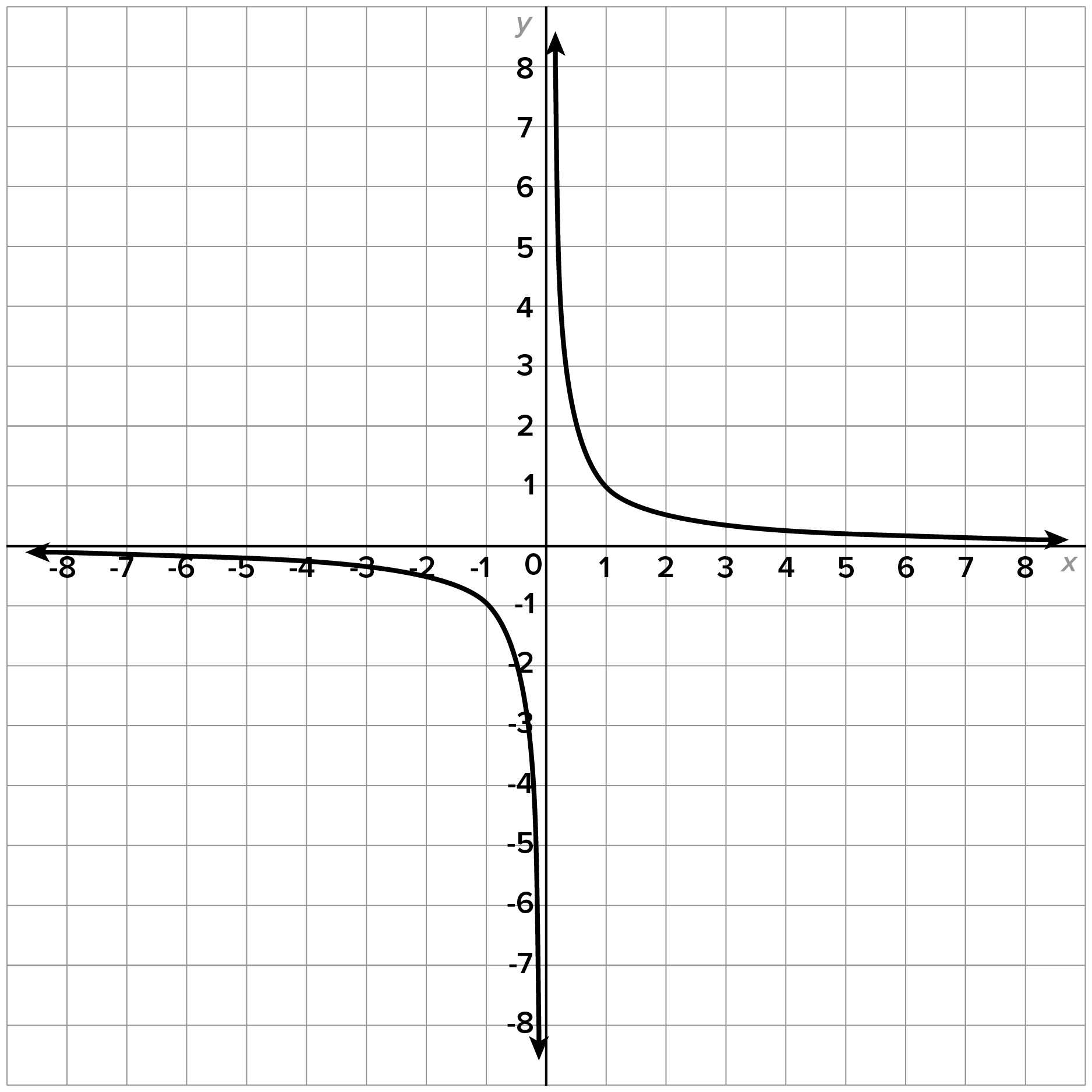
Consider the graph of 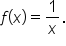
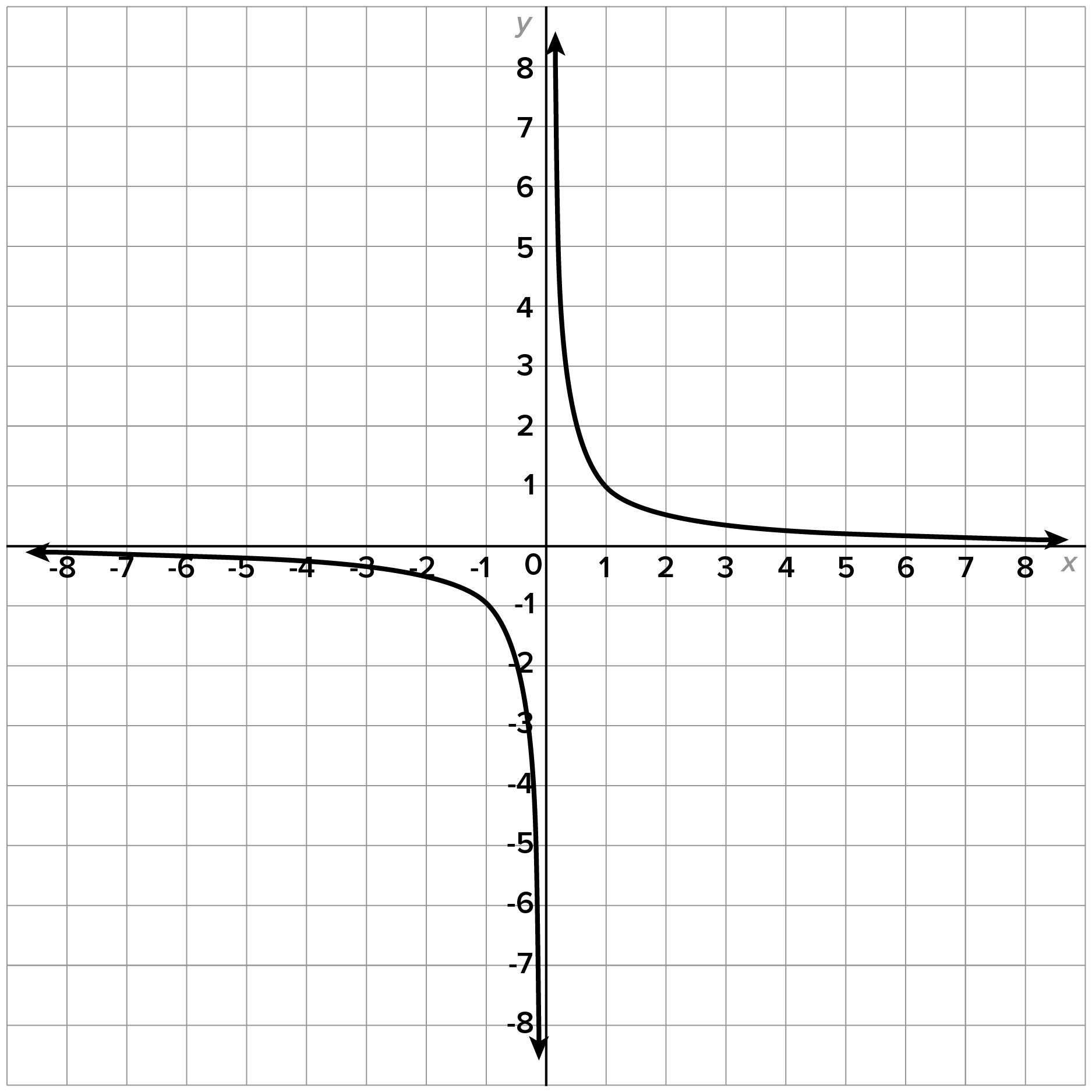
Now focus on the graph around 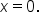
Notice how the graph falls indefinitely as x gets closer to 0 from the left side and rises indefinitely as x gets closer to 0 from the right side.
Using arrow notation, we say that 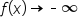 as
as 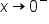 , and
, and 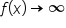 as
as 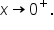
If we were to draw the line 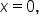 the graph would approach this line as x gets closer to 0 from either side. This line is called a vertical asymptote.
the graph would approach this line as x gets closer to 0 from either side. This line is called a vertical asymptote.
 never crosses a vertical asymptote.
never crosses a vertical asymptote.
Now consider the function 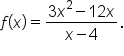
Note that this function is undefined when 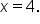 This means that the domain is
This means that the domain is  Let’s now examine the behavior of this graph around
Let’s now examine the behavior of this graph around 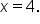

|
3.9 | 3.99 | 3.999 | 4.001 | 4.01 | 4.1 |
|---|---|---|---|---|---|---|
|
11.7 | 11.97 | 11.997 | 12.003 | 12.03 | 12.3 |
Note also that  can be simplified by removing a common factor:
can be simplified by removing a common factor:
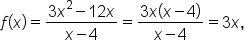 where
where 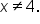
 is a line except when
is a line except when 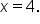 Its graph is shown below.
Its graph is shown below.
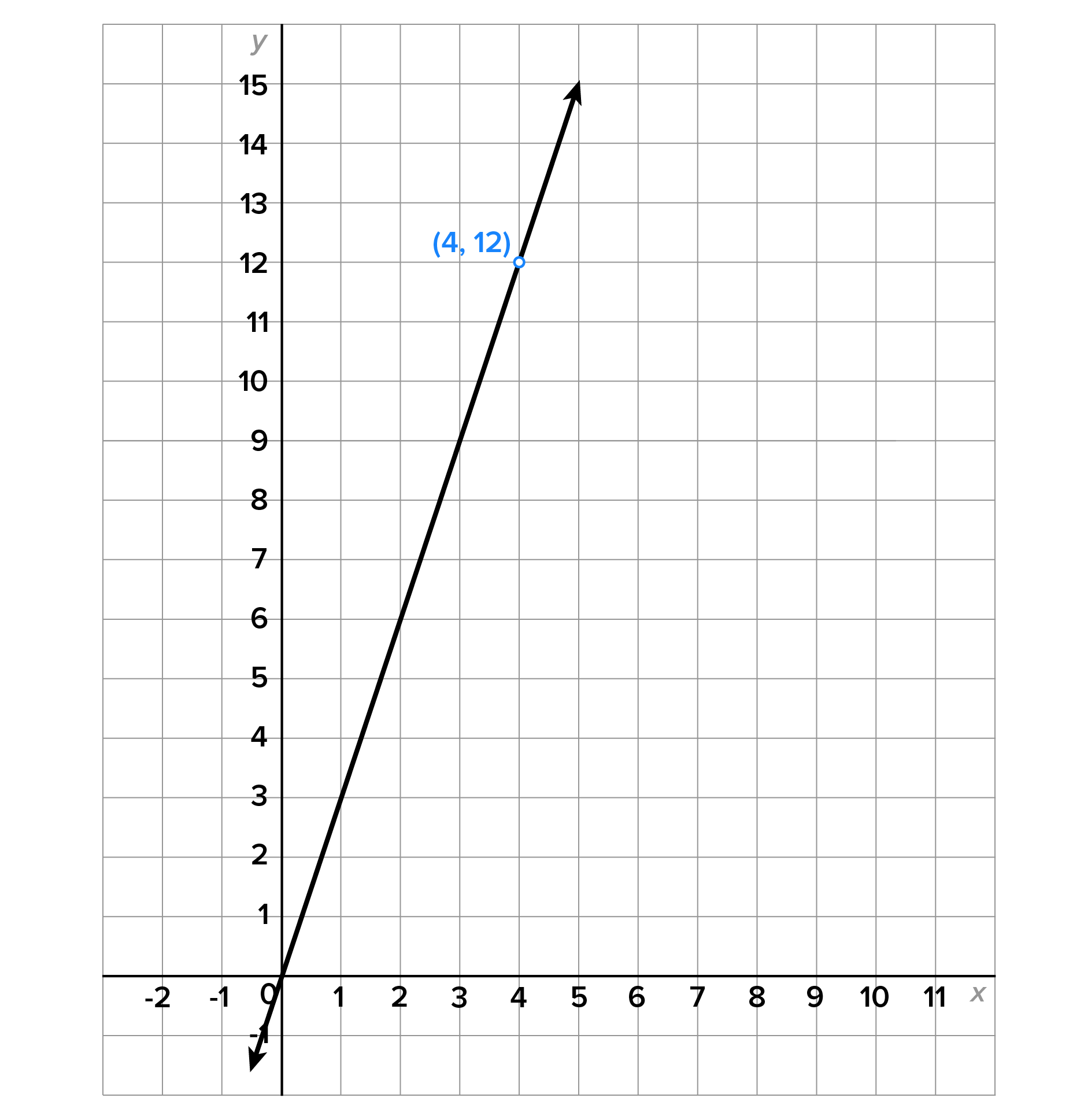
Notice the hole in the graph at 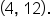 The graph has a hole in it since there is no definition for
The graph has a hole in it since there is no definition for  when
when 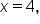 and the graph doesn’t rise or fall indefinitely as x gets closer to 4.
and the graph doesn’t rise or fall indefinitely as x gets closer to 4.
To summarize, the vertical asymptotes and holes in the graph correspond to the values of x for which the function  is undefined. So, how can we tell when the graph of a function will have a vertical asymptote and when there will be a hole in the graph?
is undefined. So, how can we tell when the graph of a function will have a vertical asymptote and when there will be a hole in the graph?
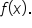
 is undefined. In other words, the denominator is equal to zero.
is undefined. In other words, the denominator is equal to zero.  is already in simplest form, then the values found in step 1 correspond to vertical asymptotes.
is already in simplest form, then the values found in step 1 correspond to vertical asymptotes.  can be simplified, then remove common factors. Let
can be simplified, then remove common factors. Let 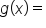 the simplified form.
the simplified form.  is equal to zero corresponds to a vertical asymptote of
is equal to zero corresponds to a vertical asymptote of 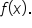
 is not equal to 0 corresponds to a hole in the graph of
is not equal to 0 corresponds to a hole in the graph of 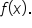 The y-coordinate of the hole in the graph is computed by substituting the value of x into
The y-coordinate of the hole in the graph is computed by substituting the value of x into 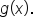
EXAMPLE
Consider the function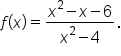 Find all vertical asymptotes and/or holes in the graph of
Find all vertical asymptotes and/or holes in the graph of 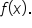
 is undefined:
is undefined:
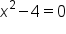
|
Set the denominator equal to 0. |
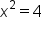 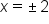
|
Solve. |
 to see if it can be simplified:
to see if it can be simplified:
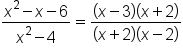
|
Factor the numerator and denominator. |
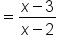
|
Remove the common factor of 
|
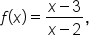 where
where 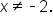 Now, let
Now, let 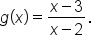
 is equal to zero when
is equal to zero when 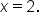 Since the numerator is not equal to zero when
Since the numerator is not equal to zero when 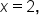 this means that
this means that 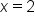 is a vertical asymptote of the graph of
is a vertical asymptote of the graph of 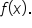
 is not equal to zero, when
is not equal to zero, when 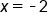 , there is a hole in the graph of
, there is a hole in the graph of  when
when 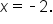
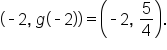
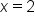 and the hole in the graph is at
and the hole in the graph is at 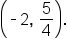
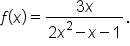
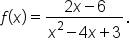
In closing, it is possible for a rational function to have neither a vertical asymptote nor a hole in the graph. This occurs when there is no real number x for which the denominator is equal to zero.
EXAMPLE
Consider the function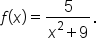
 is in simplest form.
is in simplest form.
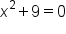
|
Set the denominator equal to 0. |
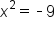 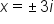
|
Solve. |
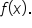
 for which
for which 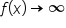 or
or 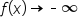 as
as 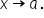
Consider the graph of 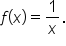
Now focus on the graph as 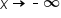 and as
and as 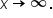 Notice how the graph appears to “level off” toward
Notice how the graph appears to “level off” toward 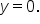
This means that the end behavior of  can be described as
can be described as 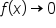 as
as 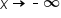 and as
and as 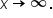
Since 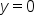 is a horizontal line, we say that the graph of
is a horizontal line, we say that the graph of  has a horizontal asymptote at
has a horizontal asymptote at 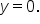
Now consider the function 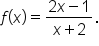
Recall that the end behavior of a polynomial is determined by its leading term. In other words:
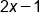 is the same as the end behavior of
is the same as the end behavior of 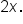
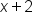 is the same as the end behavior of x.
is the same as the end behavior of x. 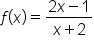 is the same as the end behavior of
is the same as the end behavior of 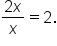
This means that 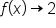 as
as 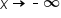 and as
and as 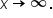
Thus, 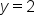 is the horizontal asymptote of
is the horizontal asymptote of 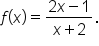
Before we summarize our findings, another example will be helpful.
EXAMPLE
Determine the horizontal asymptote of
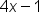 is the same as the end behavior of
is the same as the end behavior of 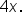
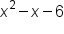 is the same as the end behavior of
is the same as the end behavior of 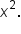
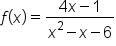 is the same as the end behavior of
is the same as the end behavior of 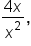 or
or 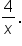
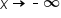 or
or 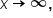
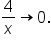 (Dividing 4 by a very large number results in a number close to 0).
(Dividing 4 by a very large number results in a number close to 0).
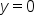 is the horizontal asymptote of
is the horizontal asymptote of 
This means that there are certain conditions under which  has a horizontal asymptote. Here is a summary.
has a horizontal asymptote. Here is a summary.
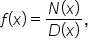 where
where 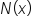 and
and 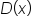 are polynomials.
are polynomials.
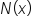 is smaller than the degree of
is smaller than the degree of 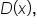 then the horizontal asymptote is
then the horizontal asymptote is 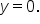
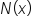 and
and 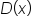 are equal, then the horizontal asymptote is
are equal, then the horizontal asymptote is 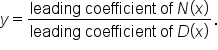
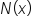 is larger than the degree of
is larger than the degree of 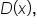 then
then  has no horizontal asymptote.
has no horizontal asymptote.
Here is an example to illustrate this important idea.
EXAMPLE
Consider the functions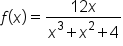 and
and 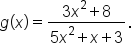
 has horizontal asymptote
has horizontal asymptote 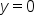 since the numerator has degree 1, which is less than the degree of the denominator, which is 3.
since the numerator has degree 1, which is less than the degree of the denominator, which is 3.
 has horizontal asymptote
has horizontal asymptote 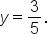 Since the degrees of the numerator and denominator of
Since the degrees of the numerator and denominator of  are the same (they are both 2), the leading coefficient of the numerator is 3, and the leading coefficient of the denominator is 5.
are the same (they are both 2), the leading coefficient of the numerator is 3, and the leading coefficient of the denominator is 5.
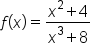 and
and 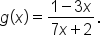
 for which
for which 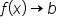 as
as 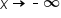 or
or 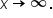
Consider a rational function 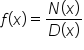 where
where 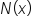 and
and 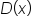 are polynomials.
are polynomials.
When the degree of 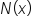 is greater than the degree of
is greater than the degree of 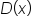 by one, then the end behavior of
by one, then the end behavior of  is described by a slant asymptote.
is described by a slant asymptote.
When the degree of 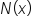 is greater than the degree of
is greater than the degree of 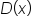 by more than one, then the end behavior of
by more than one, then the end behavior of  is described by a nonlinear asymptote.
is described by a nonlinear asymptote.
Both types are found by performing long division or when appropriate, synthetic division.
Before finding these asymptotes, let’s review the division algorithm for polynomials.
By the division algorithm, we know that 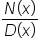 has quotient
has quotient 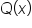 and remainder
and remainder  for which
for which  Now, let’s rewrite the equation.
Now, let’s rewrite the equation.
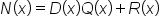
|
This is the original equation. |
|
Divide both sides by 
|
|
Simplify and replace  with with 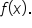
|
Remember that according to the division algorithm, the degree of  is less than the degree of
is less than the degree of 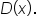 This means that
This means that 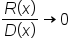 as
as 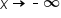 and as
and as 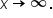
Thus, the end behavior of  is the same as the end behavior of
is the same as the end behavior of 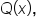 the quotient.
the quotient.
A slant asymptote is the oblique asymptote obtained when the degree of the numerator is one greater than the degree of the denominator.
EXAMPLE
Consider the function
 has a slant asymptote. To find this, we use division.
has a slant asymptote. To find this, we use division.
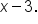 Since this is a linear term with leading coefficient equal to 1, synthetic division can be used.
Since this is a linear term with leading coefficient equal to 1, synthetic division can be used.
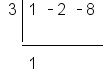
|
Set up the synthetic division. |
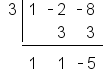
|
Perform the synthetic division. |
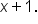 This means that the equation of the slant asymptote is
This means that the equation of the slant asymptote is 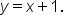
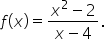
When the denominator doesn’t have the form 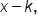 long division is used.
long division is used.
EXAMPLE
Consider the function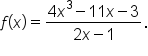
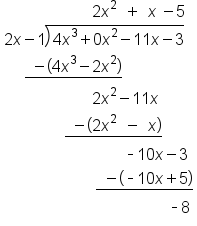
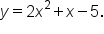
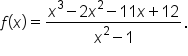
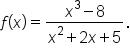
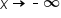 and
and 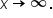
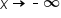 and
and 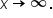
 undefined could result in vertical asymptotes or holes in the graph of a rational function. You also learned that the horizontal, slant, and nonlinear asymptotes describe the end behavior of a rational function. The graph of a rational function has either a horizontal asymptote, a slant asymptote, or a nonlinear asymptote; it is not possible for it to have more than one of these types.
undefined could result in vertical asymptotes or holes in the graph of a rational function. You also learned that the horizontal, slant, and nonlinear asymptotes describe the end behavior of a rational function. The graph of a rational function has either a horizontal asymptote, a slant asymptote, or a nonlinear asymptote; it is not possible for it to have more than one of these types.
SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.