Table of Contents |
Consider the area of the region bounded by the t-axis (horizontal axis), the function 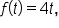 and the vertical line
and the vertical line 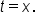 The graph is shown in the figure below.
The graph is shown in the figure below.
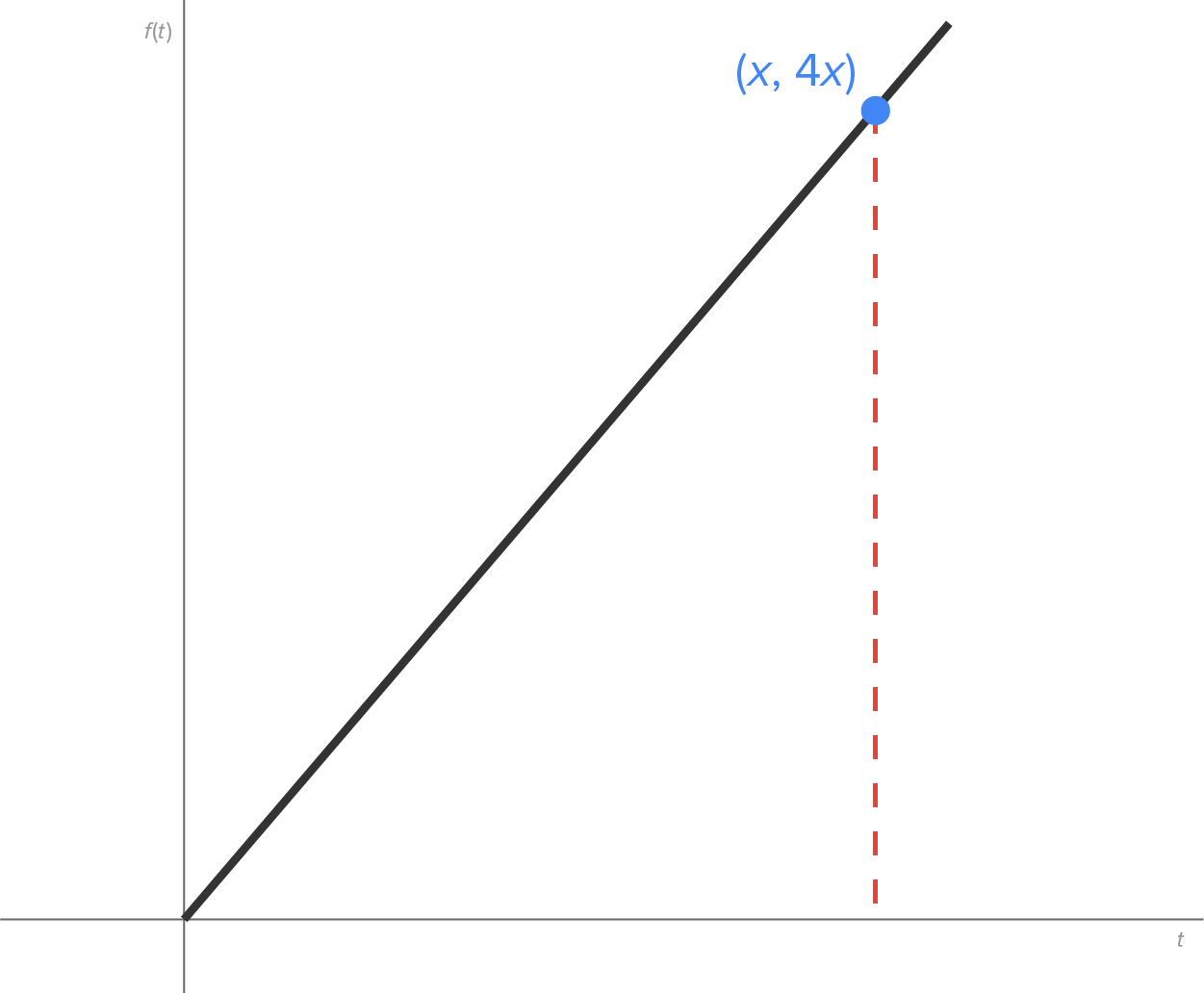
As the value of x changes, the area of the region changes, meaning that the area depends on x, meaning the area is a function of x.
Let 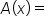 the area of the region, which is a triangle.
the area of the region, which is a triangle.
Since 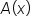 defines the area of a region between
defines the area of a region between 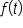 and the t-axis, we can define
and the t-axis, we can define 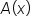 as a definite integral:
as a definite integral:
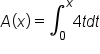
Assuming that 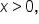 the area of the region is
the area of the region is 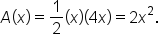
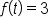 and the t-axis between
and the t-axis between 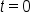 and
and 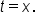
EXAMPLE
Consider the region bounded by the t-axis and the line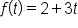 between
between 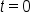 and
and 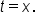
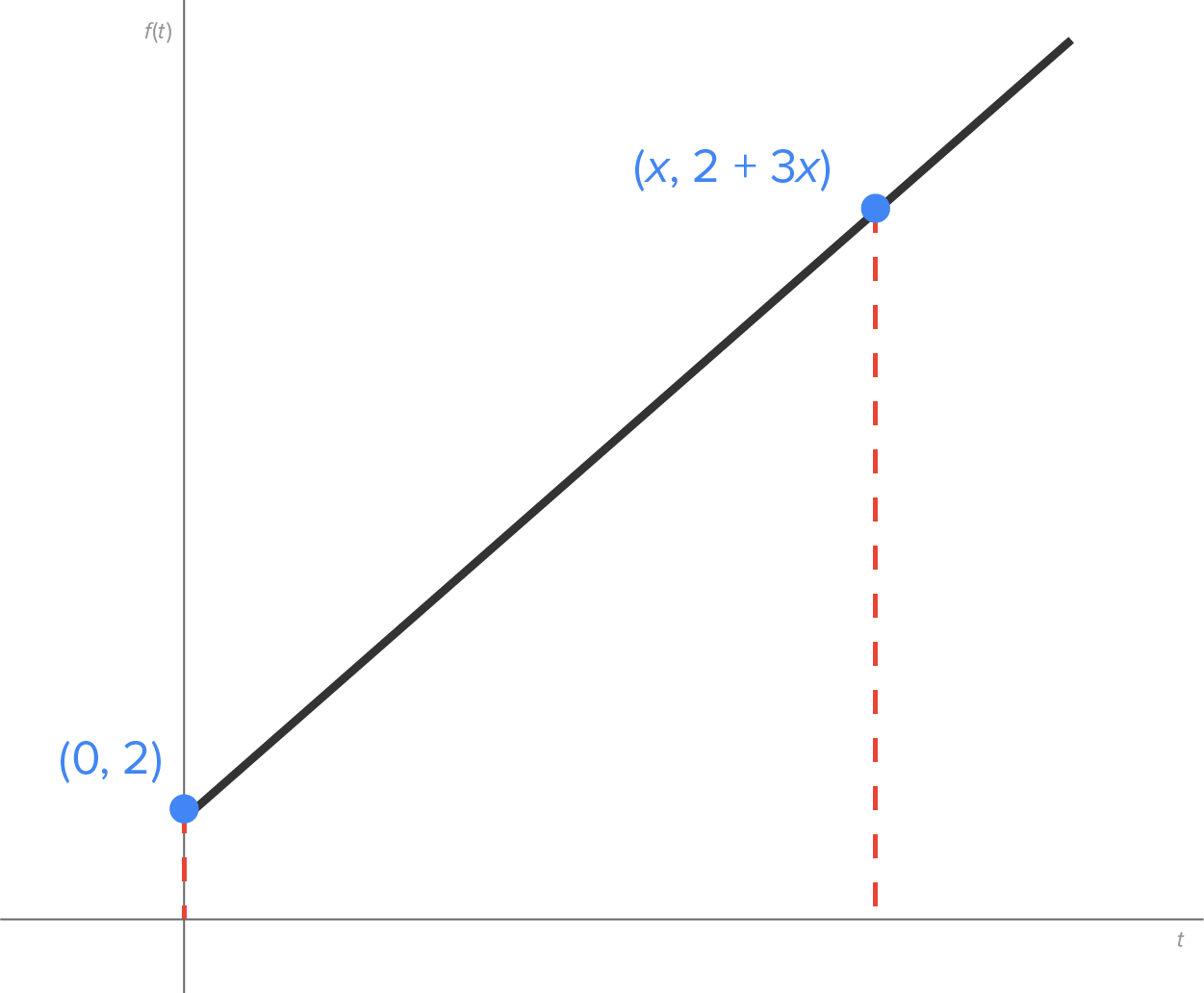
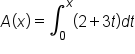
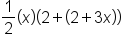
|
Use the trapezoid area formula. |
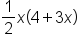
|
Simplify parentheses. |
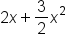
|
Distribute. |
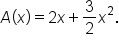
You might notice that there is a relationship between the area function 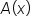 and the associated curve
and the associated curve 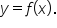 We’re going to explore this in this next segment.
We’re going to explore this in this next segment.
Consider the last three examples. Here is a summary of the area functions with their associated curves, as well as the derivatives of each area function.
| Regions |
Area Function, 
|
“Height” Function, 
|
|
|---|---|---|---|
Region bounded by the t-axis (horizontal axis), the function 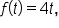 and the vertical line and the vertical line 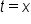
|
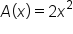
|
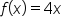
|
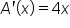
|
Region bounded by 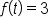 and the t-axis between and the t-axis between 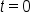 and and 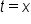
|
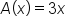
|

|
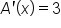
|
Region bounded by the t-axis and the line 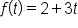 between between 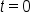 and and 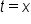
|

|
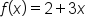
|
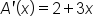
|
Note that in each situation, 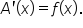 It turns out that this is always the case, which is a very useful idea in finding areas of regions that use any choice of
It turns out that this is always the case, which is a very useful idea in finding areas of regions that use any choice of 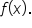 First, we need to learn a bit about antiderivatives.
First, we need to learn a bit about antiderivatives.
We call 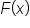 an antiderivative of
an antiderivative of  if
if 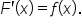 That is,
That is, 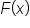 is the function whose derivative is
is the function whose derivative is 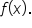 For instance, an antiderivative of
For instance, an antiderivative of 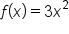 is
is 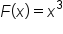 since
since 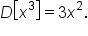 In fact, we could also say that
In fact, we could also say that 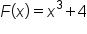 is an antiderivative of
is an antiderivative of 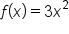 since
since 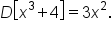
As it turns out, any function of the form 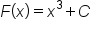 (where C is constant) is an antiderivative of
(where C is constant) is an antiderivative of 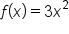 since
since 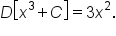
EXAMPLE
Find three antiderivatives of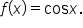
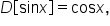 it follows that
it follows that 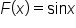 is an antiderivative of
is an antiderivative of 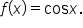 To find others, all you would need to do is add a constant.
To find others, all you would need to do is add a constant.
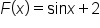 and
and 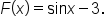
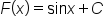 is an antiderivative of
is an antiderivative of 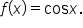
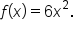
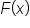 is an antiderivative of
is an antiderivative of  if
if 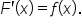
Consider the area function 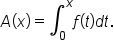
By substituting 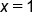 and
and 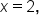 we have
we have 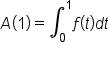 and
and 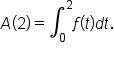
By properties of integrals, 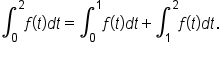
Replacing the first two integrals by their values, we have 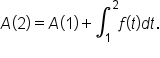
Finally, let's write the definite integral to one side: 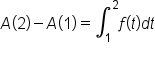
Remember that 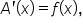 meaning that
meaning that 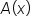 is an antiderivative of
is an antiderivative of 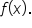 Therefore, we could write
Therefore, we could write 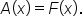
Thus, we can rewrite as 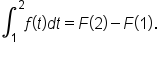 This is generalized in the first fundamental theorem of calculus, as shown below:
This is generalized in the first fundamental theorem of calculus, as shown below:
Let 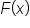 be an antiderivative of
be an antiderivative of 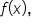 meaning that
meaning that 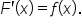 Then,
Then, 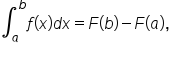 which means we evaluate the antiderivative at the endpoints, then subtract.
which means we evaluate the antiderivative at the endpoints, then subtract.
To show that we are substituting a and b into 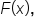 we use the following notation:
we use the following notation: 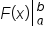
Then, it follows that 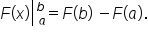
EXAMPLE
Evaluate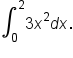
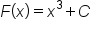 is an antiderivative of
is an antiderivative of 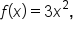 we have the following:
we have the following:
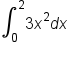
|
Start with the original expression. |
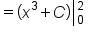
|
Apply the first fundamental theorem of calculus with 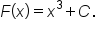
|
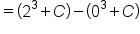
|
Substitute 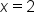 and and 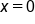 into into 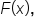 then subtract. then subtract.
|
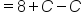
|
Evaluate operations in the parentheses. |
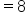
|
Simplify. |
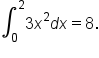
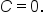 Some students even say “You don’t need the C.”
Some students even say “You don’t need the C.”
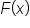 be an antiderivative of
be an antiderivative of 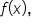 meaning that
meaning that 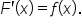
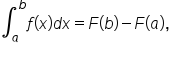 which means we evaluate the antiderivative at the endpoints, then subtract.
which means we evaluate the antiderivative at the endpoints, then subtract.Recall that 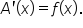 If we replace
If we replace 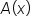 with
with 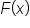 to correspond with
to correspond with 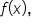 we have another important theorem in calculus, the second fundamental theorem of calculus:
we have another important theorem in calculus, the second fundamental theorem of calculus:
Let  be a continuous function on the closed interval
be a continuous function on the closed interval  with
with 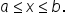
Let 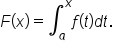 Then,
Then, 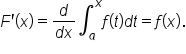
EXAMPLE
Let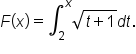
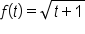 is continuous on
is continuous on 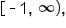 which includes 2, then
which includes 2, then 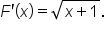
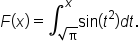
Suppose x is replaced by u, where u is a function of x.
That is, 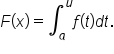 Then, by the chain rule,
Then, by the chain rule, 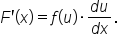
EXAMPLE
Let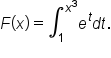
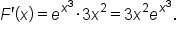
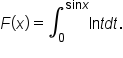
 be a continuous function on the closed interval
be a continuous function on the closed interval  with
with 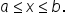
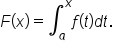 Then,
Then, 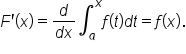
As a result of the fundamental theorem of calculus, we have a new way to compute areas with definite integrals. Instead of relying on a sketch of the region, we can use antiderivatives to compute areas.
EXAMPLE
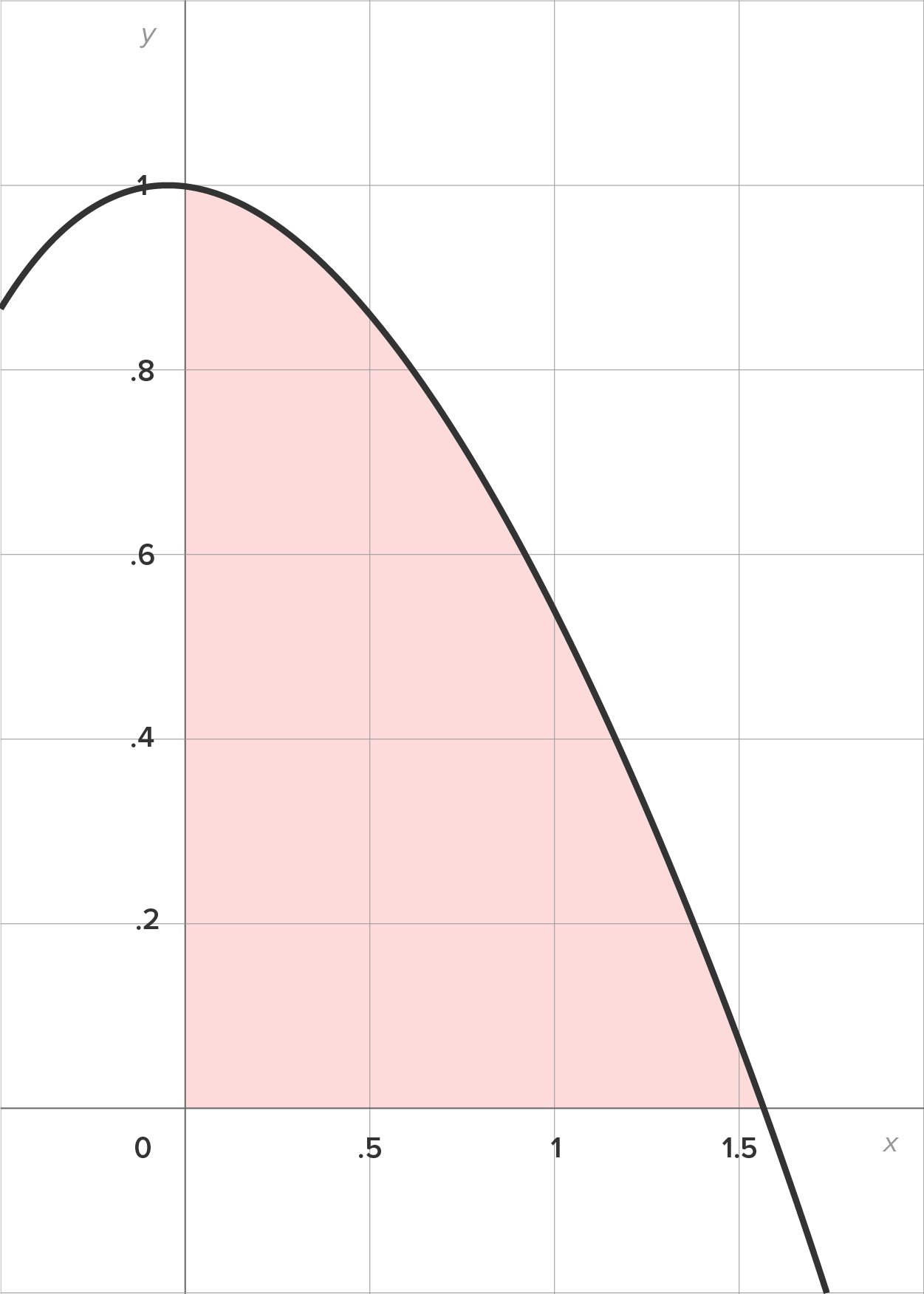
Find the area between the graph of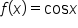 and the x-axis between
and the x-axis between 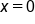 and
and 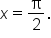 The region is shown in the figure:
The region is shown in the figure:
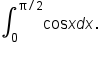
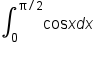
|
Start with the original expression. |
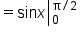
|
Use the fundamental theorem of calculus with 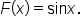 Remember, we do not need to write “+C,” meaning we are choosing Remember, we do not need to write “+C,” meaning we are choosing 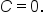
|
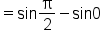
|
Substitute 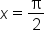 and and 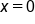 into into 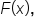 then subtract. then subtract.
|
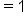
|
Simplify. Recall 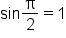 and and 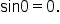
|
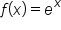 and the x-axis between
and the x-axis between 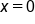 and
and 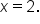
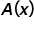 and a region with
and a region with  as the upper boundary, basic antiderivatives can be used to calculate areas and compute definite integrals by using the first and second fundamental theorems of calculus.
as the upper boundary, basic antiderivatives can be used to calculate areas and compute definite integrals by using the first and second fundamental theorems of calculus.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 4 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.