Table of Contents |
When you combine our knowledge of antiderivatives with the tables of integrals from the last tutorial, there are still functions for which we do not know antiderivatives.
EXAMPLE
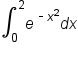 cannot be evaluated exactly since the antiderivative of
cannot be evaluated exactly since the antiderivative of 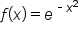 can’t be written in terms of the functions we are familiar with in calculus.
can’t be written in terms of the functions we are familiar with in calculus.
Recall in challenge 5.2, we approximated definite integrals by using rectangles of equal width along the x-axis.
Consider a nonnegative function 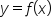 on the interval
on the interval 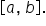 Break the interval
Break the interval 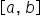 into n equal subintervals; then, each subinterval has width
into n equal subintervals; then, each subinterval has width 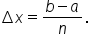
Note, these approximation methods can be used whether 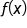 is positive, negative, or both on the interval
is positive, negative, or both on the interval 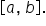 We are considering only nonnegative functions for now to make the visual connection with the area between
We are considering only nonnegative functions for now to make the visual connection with the area between 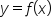 and the x-axis on
and the x-axis on 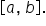
The graph below shows the interval 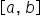 broken into 4 subintervals, where the left-hand endpoints are used to determine the height of each rectangle.
broken into 4 subintervals, where the left-hand endpoints are used to determine the height of each rectangle.
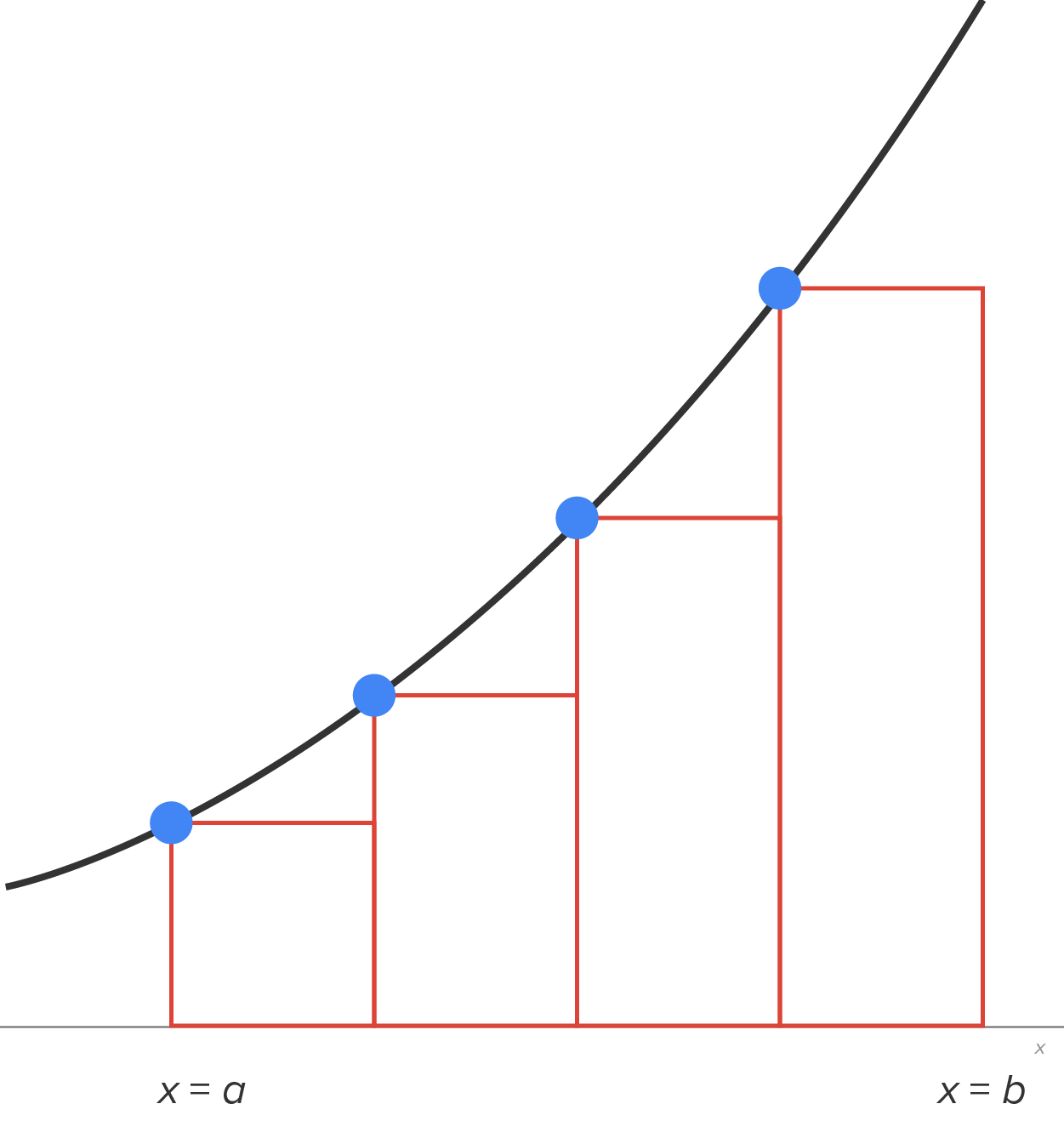
Naturally, as the number of rectangles (subintervals), n, gets larger, the approximation gets closer to the actual area (in this case, also the definite integral).
Now that we have our framework, let’s look at an example where we use all three approximation methods.
EXAMPLE
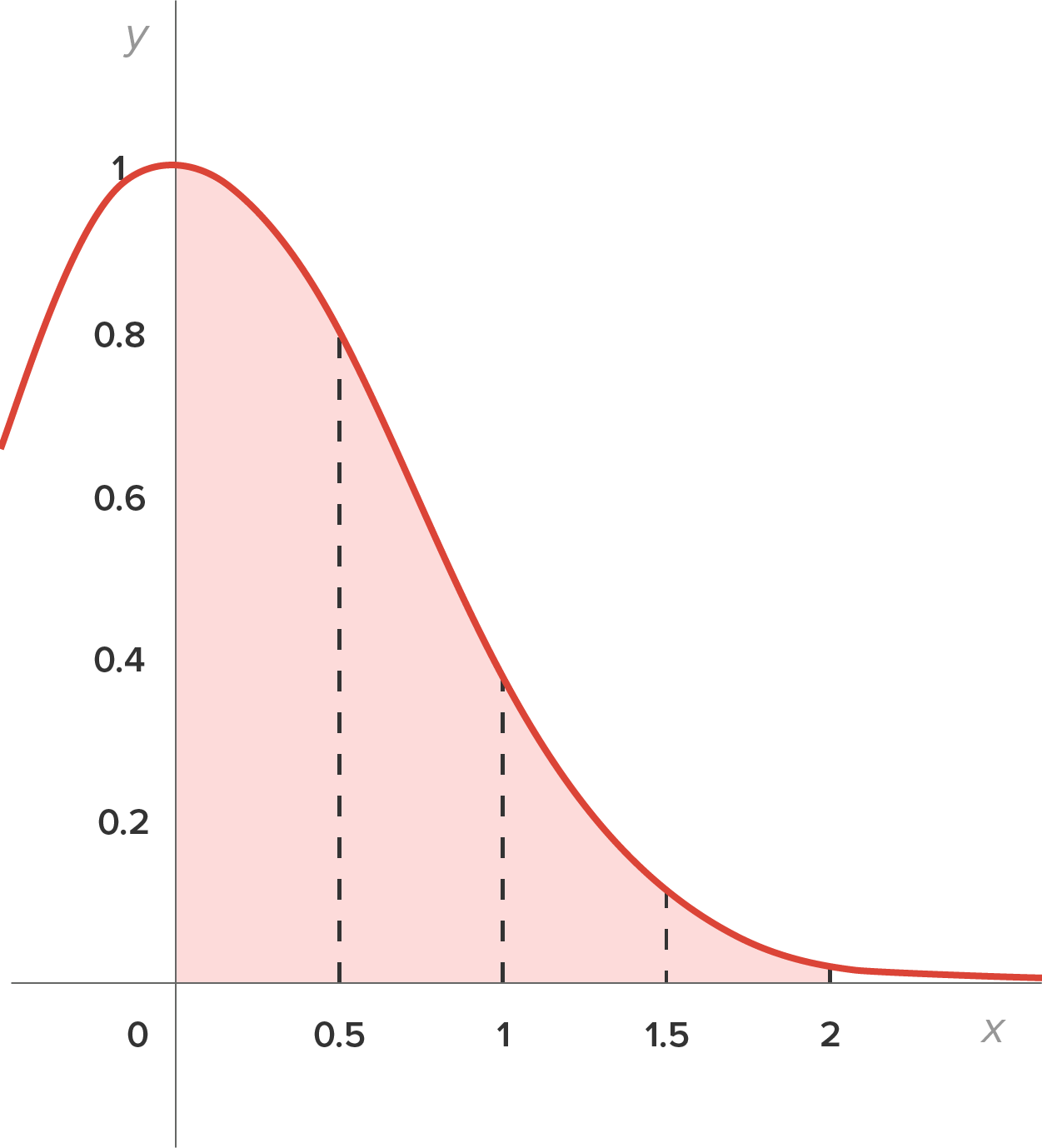
Estimate the value of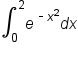 by using
by using 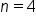 subintervals of equal width using (a) left-hand endpoints, (b) right-hand endpoints, and (c) midpoints of each subinterval.
subintervals of equal width using (a) left-hand endpoints, (b) right-hand endpoints, and (c) midpoints of each subinterval.
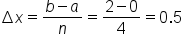 This means the subintervals are
This means the subintervals are 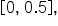
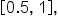
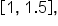 and
and 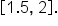
| Points | Value |
|---|---|
| Left-hand endpoints |
Using the left-hand endpoint of each interval, this means the x-values are 0, 0.5, 1, and 1.5.
Then, the estimate for the definite integral is 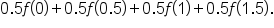
Note that we can factor out 0.5: 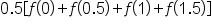 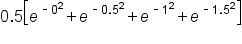
After using a calculator, this is approximately 1.12604 (to five decimal places). |
| Right-hand endpoints |
Using the right-hand endpoint of each interval, this means the x-values are 0.5, 1, 1.5, and 2.
Then, the estimate for the definite integral is 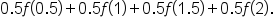
Note that we can factor out 0.5: 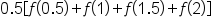 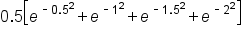
After using a calculator, this is approximately 0.63520 (to five decimal places). |
| Midpoints |
Using the midpoint of each interval, this means the x-values are 0.25, 0.75, 1.25, and 1.75.
Then, the estimate for the definite integral is 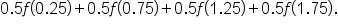
Note that we can factor out 0.5: 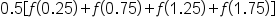 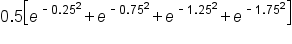
After using a calculator, this is approximately 0.88279 (to five decimal places). |
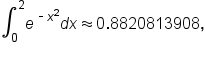 so the midpoint estimate was very close!
so the midpoint estimate was very close!
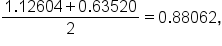 which is indeed closer.
which is indeed closer.
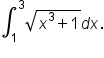
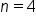 subintervals, estimate the definite integral using left-hand endpoints, right-hand endpoints, and midpoints of each subinterval. Round each estimate to 5 decimal places.
subintervals, estimate the definite integral using left-hand endpoints, right-hand endpoints, and midpoints of each subinterval. Round each estimate to 5 decimal places.
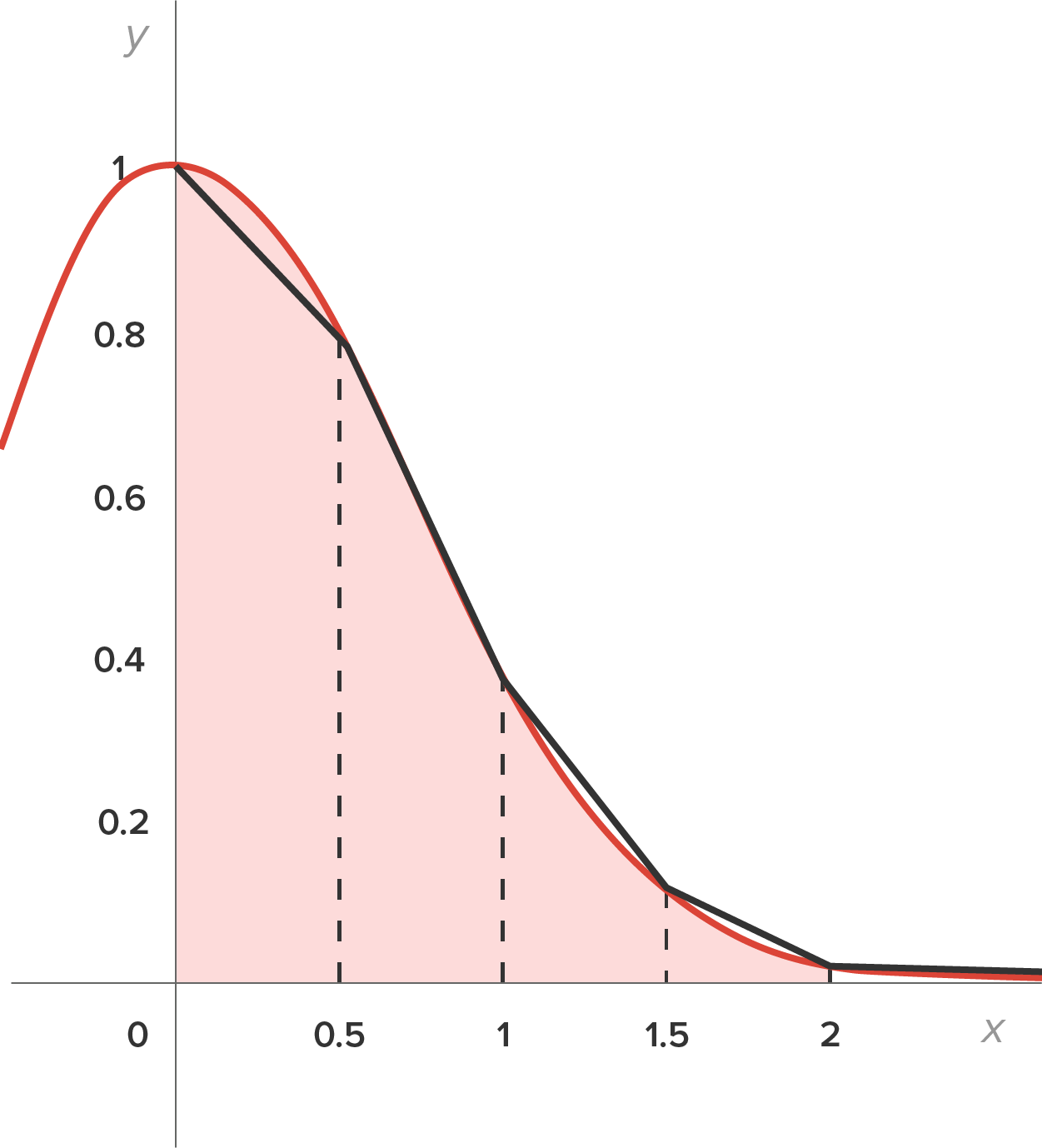
Consider the region shown in the figure, this time connecting consecutive points with a line.
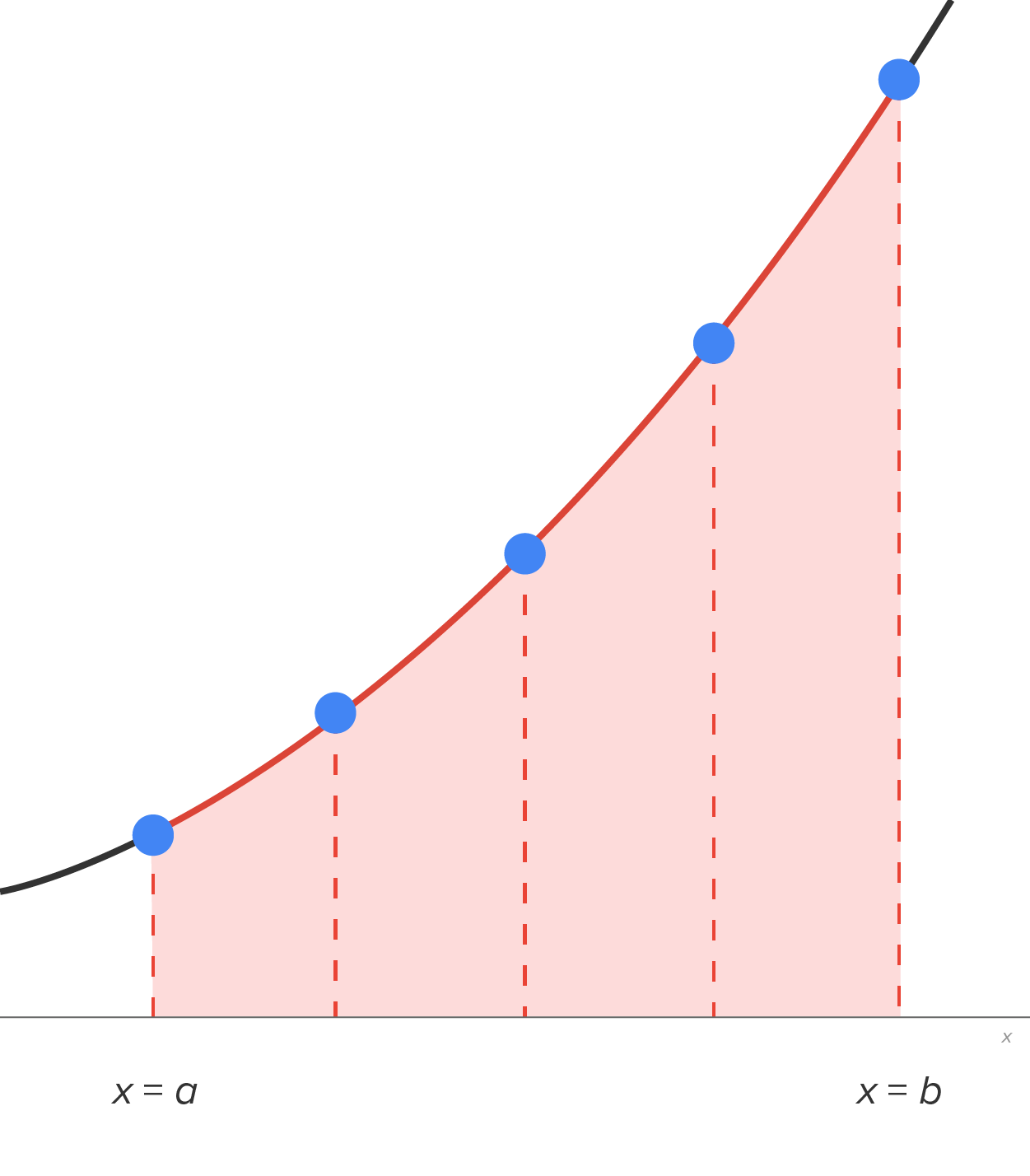
This means that trapezoids are used to approximate the area of the region in each subinterval. Recall that the area of a trapezoid is 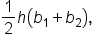 where h is the height (the distance between the parallel sides) and
where h is the height (the distance between the parallel sides) and 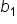 and
and 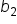 are parallel bases.
are parallel bases.
In this case, the height is the width of each trapezoid 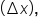 and the bases are the function values on both sides.
and the bases are the function values on both sides.
Let 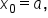
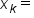 the right-hand endpoint of each subinterval, and
the right-hand endpoint of each subinterval, and 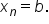
| Trapezoid | Bases | Height | Area |
|---|---|---|---|
First trapezoid on the interval 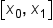
|
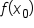 and and 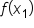
|
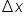
|
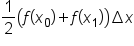
|
Second trapezoid on the interval 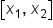
|
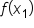 and and 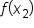
|
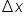
|
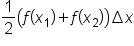
|
Third trapezoid on the interval 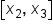
|
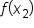 and and 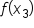
|
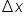
|
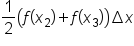
|
Last trapezoid on the interval 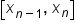
|
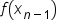 and and 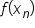
|
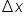
|
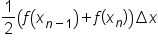
|
Notice that the endpoints (a and b) are only used in one trapezoid each. All the interior values of x are used in two trapezoids.
To estimate 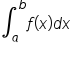 (assuming
(assuming 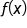 is nonnegative), add all the areas together:
is nonnegative), add all the areas together:
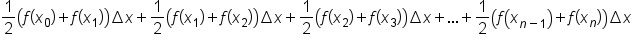
Notice that each quantity has a factor of 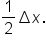 We’ll factor this out:
We’ll factor this out:
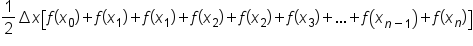
There are some like terms within the brackets. Combine them:
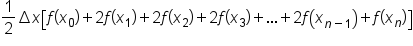
Note: we know that the 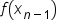 term will show up twice since it is a base in each of the last two trapezoids.
term will show up twice since it is a base in each of the last two trapezoids.
This leads to a formula for estimating 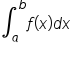 using trapezoids. This method is aptly named the trapezoidal rule.
using trapezoids. This method is aptly named the trapezoidal rule.
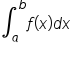 can be approximated by the sum
can be approximated by the sum 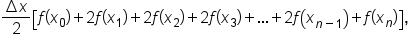 where
where 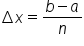 and
and 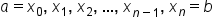 are the endpoints of each equally spaced subinterval.
are the endpoints of each equally spaced subinterval.EXAMPLE
Estimate the value of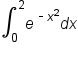 by using
by using 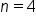 subintervals of equal width using the trapezoidal rule. Check that this is equal to the average of the left- and right-hand endpoint estimates.
subintervals of equal width using the trapezoidal rule. Check that this is equal to the average of the left- and right-hand endpoint estimates.
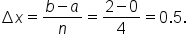 This means the subintervals are
This means the subintervals are 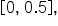
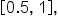
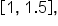 and
and 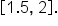
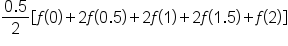
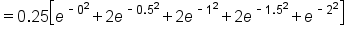
In an earlier example, we also computed the average of the left- and right-hand estimates, and this was also approximately 0.88062. (If you look beyond the third decimal place in each, the estimates should be identical.)
While the methods discussed so far seem to do a fair job of approximating 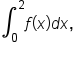 it makes more sense to approximate
it makes more sense to approximate  with a curve rather than a straight line (if
with a curve rather than a straight line (if  is a straight-line function, there is no need to approximate the definite integral). To that end, we can also use parabolas, but not before we establish a rule for the definite integral of a parabola.
is a straight-line function, there is no need to approximate the definite integral). To that end, we can also use parabolas, but not before we establish a rule for the definite integral of a parabola.
If  then
then 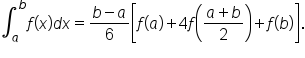
Now, consider this region.
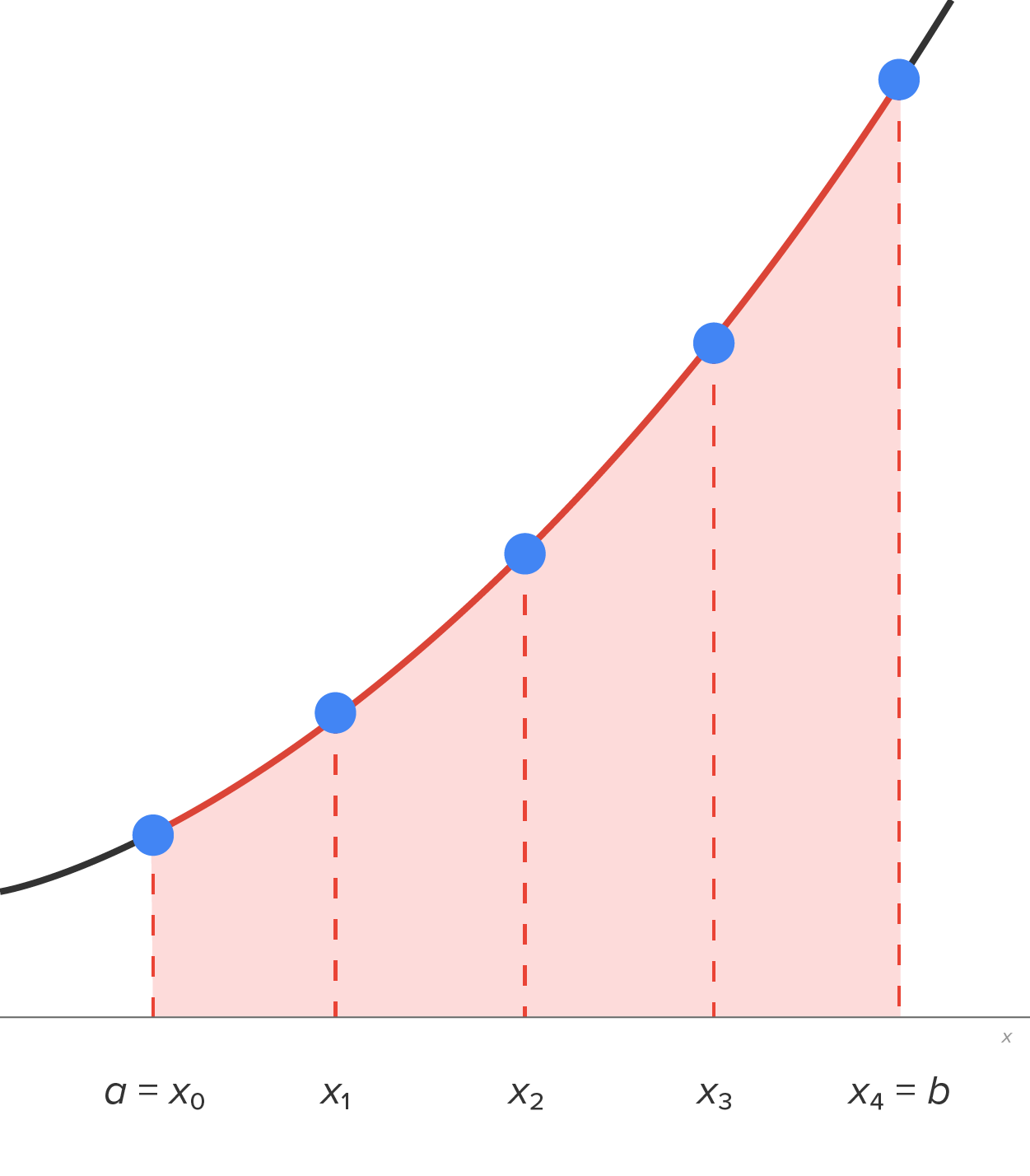
If we want to approximate 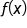 by using a parabola, we would have
by using a parabola, we would have 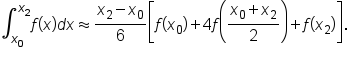
Note: 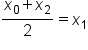 (that is, since the x-values are evenly spaced,
(that is, since the x-values are evenly spaced, 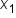 is the average of
is the average of 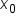 and
and 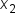 ).
).
Also, consider the quantity 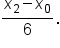 Since
Since 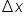 is the distance between two consecutive x-values, it follows that
is the distance between two consecutive x-values, it follows that 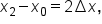 which means
which means 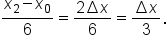
Thus, we can write 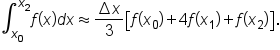
Then, considering the interval 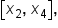 we have
we have 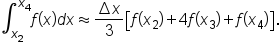
Then, the approximation for 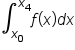 is the sum of the previous two approximations:
is the sum of the previous two approximations:
That is, 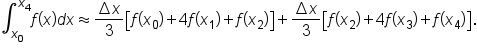
Factoring out 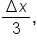 this becomes
this becomes 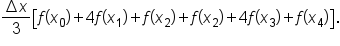
Combining like terms, this becomes 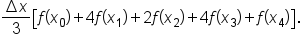
Note: since each parabola uses two subintervals, the number of subintervals must be even.
If this process were to continue, notice the following:
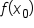 and
and 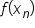 would have coefficients of 1.
would have coefficients of 1.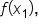
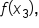 ... would have coefficients of 4 (odd-numbered subscripts).
... would have coefficients of 4 (odd-numbered subscripts).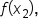
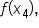 ... would have coefficients of 2 (even-numbered subscripts, but not the endpoints).
... would have coefficients of 2 (even-numbered subscripts, but not the endpoints).This approximation method is known as Simpson’s rule.
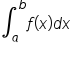 is approximated by
is approximated by 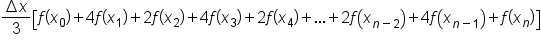 where
where 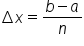 and
and 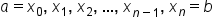 are the endpoints of each equally spaced subinterval. Note: n must be even.
are the endpoints of each equally spaced subinterval. Note: n must be even.EXAMPLE
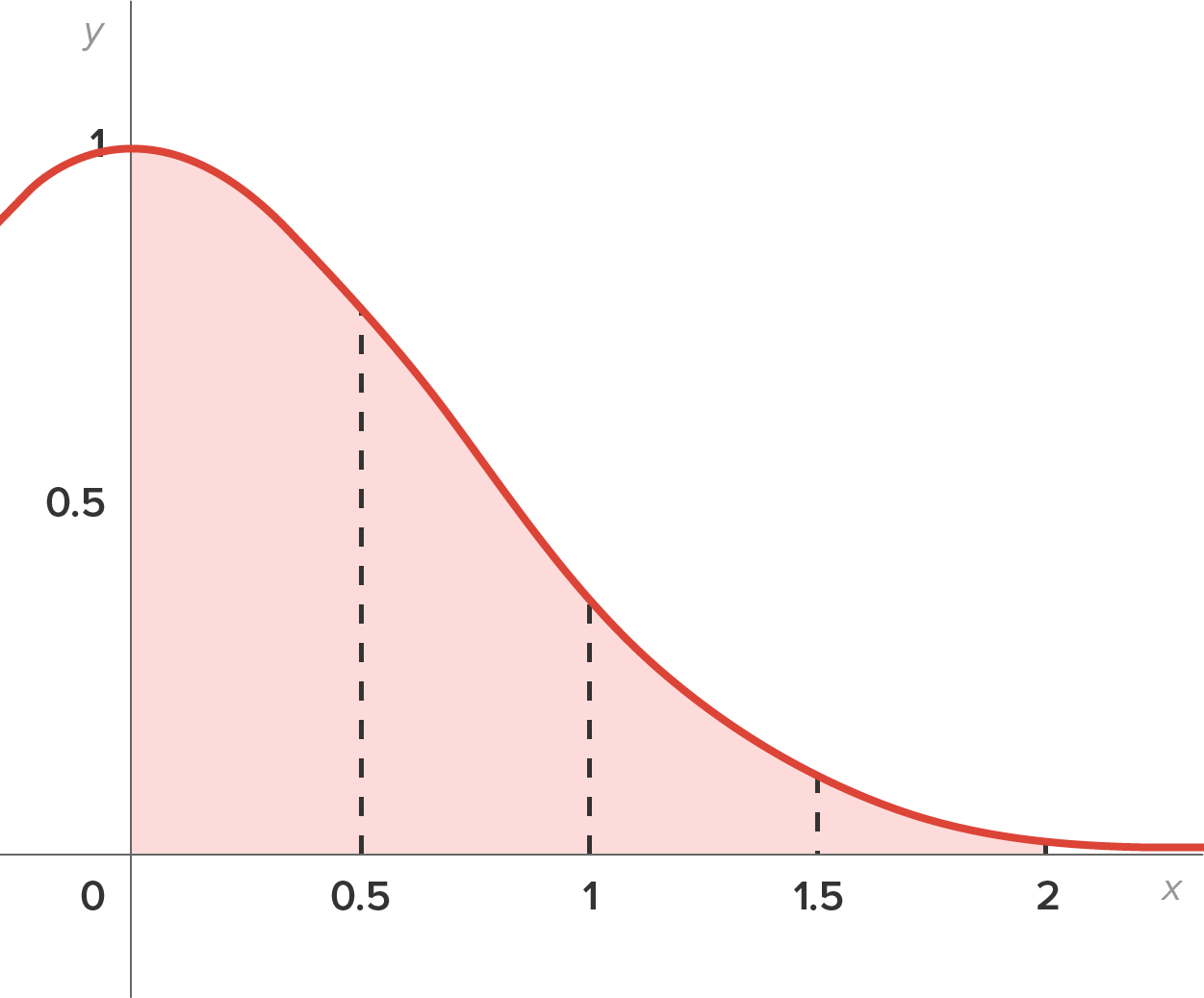
Estimate the value of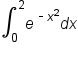 by using
by using 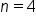 subintervals of equal width using Simpson’s rule.
subintervals of equal width using Simpson’s rule.
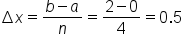 . This means the subintervals are
. This means the subintervals are 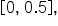
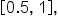
 and
and 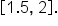
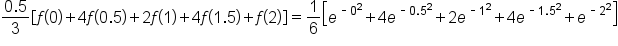
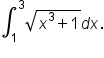
The approximation methods shown in this challenge are all used to approximate the value of a definite integral. Using that connection, these methods can be used to approximate the area of an irregularly shaped region, as we’ll see in the next part.
EXAMPLE
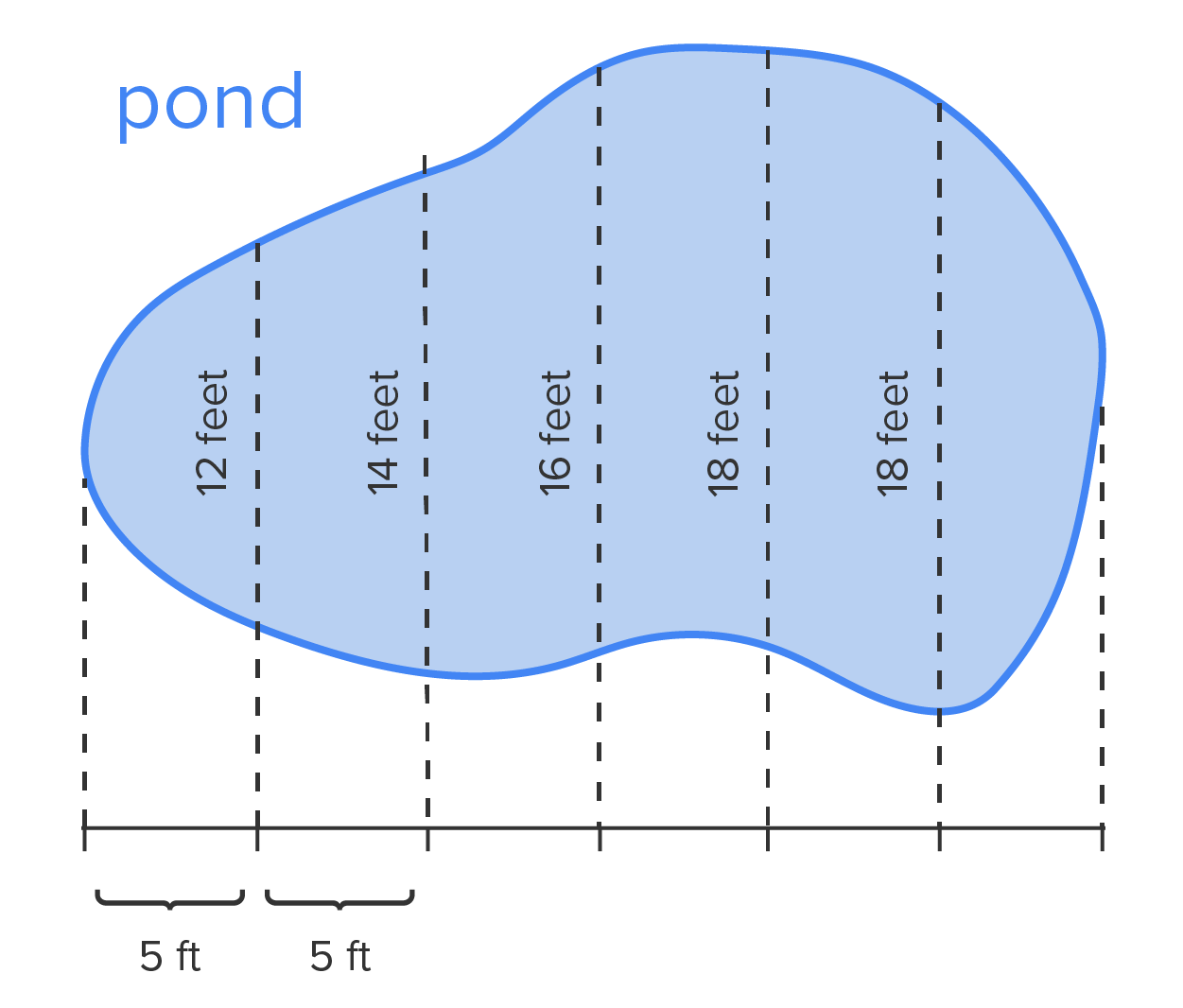
Suppose the measurements of a park are shown below. What is the approximate area of the park? As the figure suggests, the measurements were taken every 30 feet.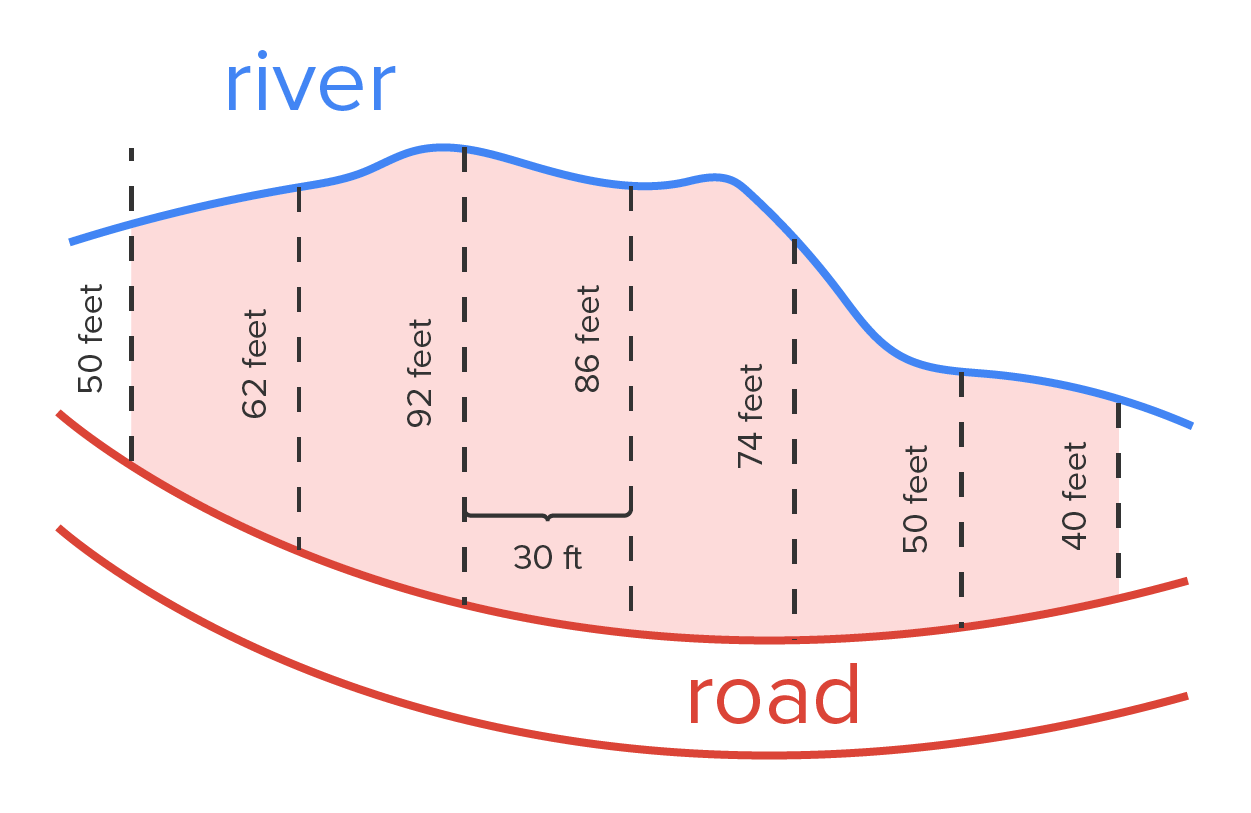
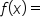 the length of the park at a distance of x feet from the left-hand side (as shown). Then, the area of the park is
the length of the park at a distance of x feet from the left-hand side (as shown). Then, the area of the park is 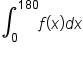 (there are 6 widths of 30 feet, for a total of 180 feet).
(there are 6 widths of 30 feet, for a total of 180 feet).
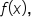 we’ll need to use the approximation techniques learned in this section to estimate the area.
we’ll need to use the approximation techniques learned in this section to estimate the area.
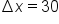 with
with 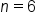 subintervals, we can easily use the left-hand and right-hand endpoints, the trapezoidal rule and Simpson’s rule to approximate the area. (Since we don’t know the values of
subintervals, we can easily use the left-hand and right-hand endpoints, the trapezoidal rule and Simpson’s rule to approximate the area. (Since we don’t know the values of  in the middle of each interval, the midpoint method cannot be used.)
in the middle of each interval, the midpoint method cannot be used.)
|
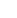
|
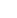
|
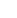
|
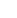
|
|
|
|
|---|---|---|---|---|---|---|---|

|
0 | 30 | 60 | 90 | 120 | 150 | 180 |
| Length | 50 | 62 | 92 | 86 | 74 | 50 | 40 |
| Method | Estimation for the Area |
|---|---|
| Left-Hand Endpoints |
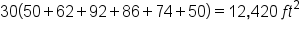
|
| Right-Hand Endpoints |
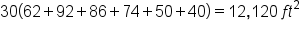
|
| Trapezoids |
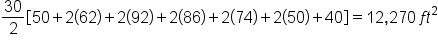
|
| Simpson's Rule |
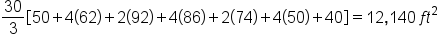
|
 but since not all curves are parabolic, there is still room for some error. In all cases, the estimate is improved by increasing the number of subintervals. Finally, you were able to apply the techniques learned in this section to approximate the area in several examples.
but since not all curves are parabolic, there is still room for some error. In all cases, the estimate is improved by increasing the number of subintervals. Finally, you were able to apply the techniques learned in this section to approximate the area in several examples.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 4 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.