Table of Contents |
The form 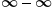 occurs when there is a difference between two expressions that are both tending toward
occurs when there is a difference between two expressions that are both tending toward 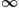 as
as 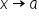 .
.
EXAMPLE
Evaluate the following limit: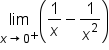
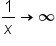 and
and 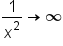 as
as 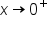 , we have a limit of the form
, we have a limit of the form 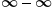 . One strategy is to write it as a single fraction, since this is a more familiar scenario.
. One strategy is to write it as a single fraction, since this is a more familiar scenario.
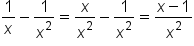 , we have the following:
, we have the following:
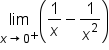
|
Start with the limit that needs to be evaluated. |
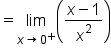
|
Replace the expression with a single fraction. |
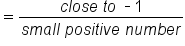
|
As x approaches 0 from the right, x - 1 approaches -1 and 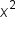 is a small positive number. is a small positive number.
|
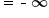
|
A negative number divided by a small positive number is a large negative number. |
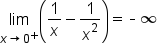 .
.
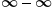 should be 0 since you are “subtracting something from itself.” As we can see, this is not the case. Once we see
should be 0 since you are “subtracting something from itself.” As we can see, this is not the case. Once we see 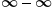 produce another value, we will see why it is an indeterminate form.
produce another value, we will see why it is an indeterminate form.
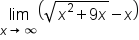 .
.
Considering the results from these last two examples, it is clear now why 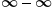 is an indeterminate form. In one case, the result was
is an indeterminate form. In one case, the result was 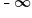 , and in another case, the result was
, and in another case, the result was 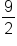 .
.
The indeterminate form 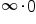 is handled in one of two ways.
is handled in one of two ways.
Loosely speaking, we can say that a limit of the form 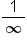 will approach 0 and a limit of the form
will approach 0 and a limit of the form 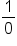 will approach
will approach 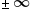 .
.
That said, we can treat “0” and “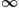 ” as reciprocals as far as limits are concerned.
” as reciprocals as far as limits are concerned.
This means that the indeterminate form 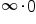 could be rewritten as either
could be rewritten as either  or
or 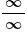 , whichever is more convenient.
, whichever is more convenient.
EXAMPLE
Evaluate the following limit: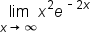
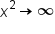 and
and 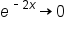 as
as 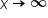 . Thus, this limit has the form
. Thus, this limit has the form 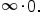
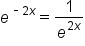 , which means
, which means 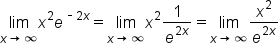 , which now has the form
, which now has the form 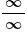 .
.
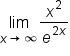
|
Start with the limit that needs to be evaluated. |
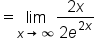
|
Since 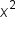 and and 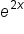 are differentiable and the limit has the form are differentiable and the limit has the form 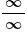 , L’Hopital’s rule is used. , L’Hopital’s rule is used.
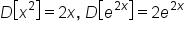
|
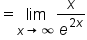
|
Remove the common factor of 2. |
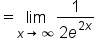
|
Since 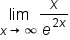 has the form has the form 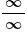 , continue to use L’Hopital’s rule. , continue to use L’Hopital’s rule. 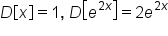
|
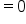
|
Since the denominator grows very large as 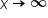 , the limit is 0. , the limit is 0.
|
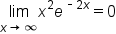 .
.
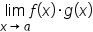 has the form
has the form 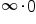 , write
, write 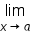
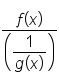 or
or 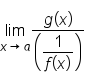 , then use L'Hopital's rule.
, then use L'Hopital's rule.
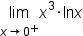 .
.
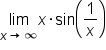 .
.
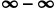 , combining the fractions or rationalizing are the most common strategies; for the indeterminate form
, combining the fractions or rationalizing are the most common strategies; for the indeterminate form 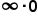 , rewriting the expression using reciprocals then using L’Hopital’s rule is the main strategy.
, rewriting the expression using reciprocals then using L’Hopital’s rule is the main strategy.
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 3 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.