Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Annual Percentage Yield (APY)

Author: Sophia
PDF Version

what's covered
In this lesson, you will define and calculate annual percentage yield. Specifically, this lesson will cover:

Table of Contents

1. Annual Percentage Yield (APY)

To begin our discussion of annual percentage yield (APY), let’s consider two scenarios:

  • An investment of $1,000 earns $42.50 in interest in its first year.
  • An investment of $3,500 earns $100 in interest in its first year.
One measure of how well an investment is doing is to know the percentage rate at which interest is earned in one year, which is called the annual percentage yield.

Conceptually, the APY is the amount of money earned each year for every dollar invested. A more convenient way to express APY is as a percent.

formula to know
Annual Percentage Yield (APY)
APY equals fraction numerator Interest space Earned space in space One space Year over denominator Principal end fraction. To convert this to a percent, multiply by 100.

Note that this formula means that we compute the APY by first dividing the interest by the principal, then multiplying by 100 to convert to a percent, round to the desired number of decimal places, then affix the percent symbol.

EXAMPLE

Find the APY for an investment of $1,000 that earns $42.50 in interest per year.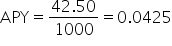

By the APY formula, APY equals fraction numerator 42.50 over denominator 1000 end fraction equals 0.0425.

Converting to a percent, the APY is 4.25%.

Note that the decimal form, 0.0425 means that 0.0425 dollars in interest (which is 4.25 cents) are earned for every $1 invested. Notice that this also means 4.25 cents for every 100 cents, which leads nicely to using the percent form (per hundred).

try it

Find the APY for an investment of $3,500 that earns $100 in interest per year. If needed, write your final answer as a percent rounded to two decimal places.
By the APY formula, APY equals 100 over 3500 equals 0.028571428...

Multiplying by 100%, we have APY equals 2.8571428 horizontal ellipsis. percent sign, which rounds to 2.86%.

By comparing the APY’s in the example and in the “TRY IT,” we see that the first investment is earning a higher annual interest rate. Even though the amount of interest is lower, it was based on a smaller principal.

2. Finding APY for Investments in Which Interest Is Compounded n Times Per Year

Suppose $200 is invested into an account at an annual interest rate of 4%, compounded monthly. Let’s find the amount in the account after 1 year.

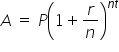
A space equals space P open parentheses 1 plus r over n close parentheses to the power of n t end exponent The compound interest formula.
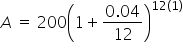
A space equals space 200 open parentheses 1 plus fraction numerator 0.04 over denominator 12 end fraction close parentheses to the power of 12 open parentheses 1 close parentheses end exponent Substitute P = 200, r = 0.04, and n = 12.
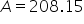
A equals 208.15 Use a calculator to approximate.

So, after 1 year, there is $208.15 in the account.

Knowing that $200 was invested, anything additional is interest earned. In this case, the interest earned is 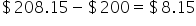$ 208.15 minus $ 200 equals $ 8.15.

What does this mean? If we know the amount in the account and the principal, we can also find the interest earned by calculating their difference.

formula to know
Interest Earned
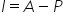I equals A minus P, where A is the amount in the account after a given length of time, and P is the principal (amount invested).

Consider a principal of P dollars invested for one year, invested at an annual interest rate r (in decimal form), where interest is compounded n times per year.

Let’s use this information to see if we can find a formula for APY.

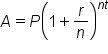
A equals P open parentheses 1 plus r over n close parentheses to the power of n t end exponent The amount in the account is found by using the compound interest formula.
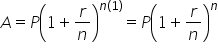
A equals P open parentheses 1 plus r over n close parentheses to the power of n left parenthesis 1 right parenthesis end exponent equals P open parentheses 1 plus r over n close parentheses to the power of n In this case, 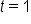t equals 1; substitute and simplify.
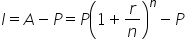
I equals A minus P equals P open parentheses 1 plus r over n close parentheses to the power of n minus P Interest is the difference between the value after one year and the principal.
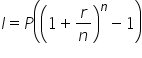
I equals P open parentheses open parentheses 1 plus r over n close parentheses to the power of n minus 1 close parentheses Remove the common factor of P.
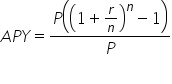
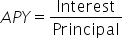
A P Y equals fraction numerator P open parentheses open parentheses 1 plus r over n close parentheses to the power of n minus 1 close parentheses over denominator P end fraction A P Y equals Interest over Principal
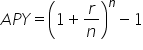
A P Y equals open parentheses 1 plus r over n close parentheses to the power of n minus 1 Cancel out the common factor of P. This is the decimal form of the APY.

hint
To get the APY, take the result and multiply by 100.

formula to know
APY for an Investment in Which Interest Is Compounded n Times Per Year
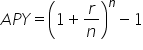A P Y equals open parentheses 1 plus r over n close parentheses to the power of n minus 1, where r = the annual interest rate (in decimal form) and n = the number of compounding periods in one year. To convert this to a percent, multiply by 100.

The formula suggests that the principal is not needed to compute the APY! All that is needed is the annual interest rate and the number of annual compounding periods there are.

EXAMPLE

Determine the APY for an investment in which the annual interest rate is 2.1% and is compounded monthly. Express the final answer as a percent rounded to the nearest hundredth.

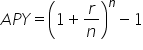
A P Y equals open parentheses 1 plus r over n close parentheses to the power of n minus 1 The APY formula.
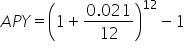
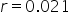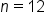A P Y equals open parentheses 1 plus fraction numerator 0.021 over denominator 12 end fraction close parentheses to the power of 12 minus 1 Substitute r equals 0.021 and n equals 12.
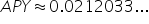
A P Y almost equal to 0.0212033... Use a calculator to approximate.
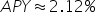
A P Y almost equal to 2.12 percent sign Multiply by 100 and round to the nearest hundredth.

This means that any investment with an annual interest rate of 2.1%, compounded monthly, will have an APY of 2.12%.

try it

Find the APY for an investment in which the annual interest rate of 7.2% is compounded quarterly. Write your final answer as a percent rounded to the nearest hundredth.
A P Y equals open parentheses 1 plus r over n close parentheses to the power of n minus 1 The APY formula.
A P Y equals open parentheses 1 plus fraction numerator 0.072 over denominator 4 end fraction close parentheses to the power of 4 minus 1 Substitute r equals 0.074 and n equals 4.
A P Y almost equal to 0.07376743... Use a calculator to approximate.
A P Y almost equal to 7.40 percent sign Multiply by 100 and round to the nearest hundredth.

This means that any investment with an annual interest rate of 7.2%, compounded quarterly, will have an APY of 7.40%.

To show that the APY remains the same for any principal that is used, compare these two investments that use an annual interest rate of 7.2%, compounded quarterly.

P = $300 P = $800,000
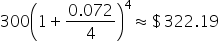
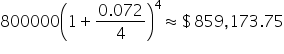
Amount after 1 year: 300 open parentheses 1 plus fraction numerator 0.072 over denominator 4 end fraction close parentheses to the power of 4 almost equal to $ 322.19 800000 open parentheses 1 plus fraction numerator 0.072 over denominator 4 end fraction close parentheses to the power of 4 almost equal to $ 859 comma 173.75
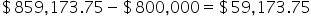
Interest earned: $ 322.19 minus $ 300 equals $ 22.19 $ 859 comma 173.75 minus $ 800 comma 000 equals $ 59 comma 173.75
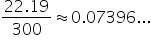
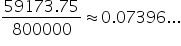
Interest over Principal fraction numerator 22.19 over denominator 300 end fraction almost equal to 0.07396... fraction numerator 59173.75 over denominator 800000 end fraction almost equal to 0.07396...
Convert to % and round: 7.40% 7.40%


hint
The minute differences in calculations are due to rounding.

3. Finding APY for Investments in Which Interest Is Compounded Continuously

Similar to how we derived the formula for APY for an investment that compounds n times per year, we can derive a formula for the APY of an investment that compounds interest continuously.

Recall that the formula for continuously compounded interest is 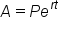A equals P e to the power of r t end exponent, where A is the amount after t years, P is the principal, and r is the annual interest rate.

Let’s use this information to see if we can find a formula for APY.

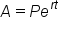
A equals P e to the power of r t end exponent The amount in the account is found by using the continuously compounded interest formula.
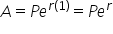
A equals P e to the power of r left parenthesis 1 right parenthesis end exponent equals P e to the power of r In this case, 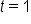t equals 1; substitute and simplify.
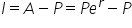
I equals A minus P equals P e to the power of r minus P Interest is the difference between the value after 1 year and the principal.
I equals P left parenthesis e to the power of r minus 1 right parenthesis Remove the common factor of P.
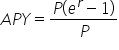
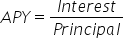
A P Y equals fraction numerator P left parenthesis e to the power of r minus 1 right parenthesis over denominator P end fraction A P Y equals fraction numerator I n t e r e s t over denominator P r i n c i p a l end fraction
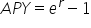
A P Y equals e to the power of r minus 1 Cancel out the common factor of P. This is the decimal form of the APY.

To get the APY, take the result and multiply by 100.

formula to know
APY for an Investment in Which Interest Is Compounded Continuously
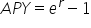A P Y equals e to the power of r minus 1, where r = the annual interest rate (in decimal form). To convert this to a percent, multiply by 100.

EXAMPLE

An investment has an annual interest rate of 5.3%, compounded continuously. Find the corresponding APY. Write your answer as a percent rounded to the nearest hundredth.

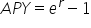
A P Y equals e to the power of r minus 1 The APY formula for continuous compounding.
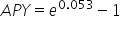
A P Y equals e to the power of 0.053 end exponent minus 1 Substitute 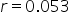r equals 0.053.
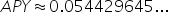
A P Y almost equal to 0.054429645... Use a calculator to approximate.
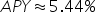
A P Y almost equal to 5.44 percent sign Multiply by 100% and round to the nearest hundredth.

This means that any investment with an annual interest rate of 5.3%, compounded continuously, will have an APY of 5.44%.

4. Comparing Investments

The APY tells us about the rate at which interest is earned each year. Therefore, the higher the APY, the higher the rate of interest. APY is a tool that can be used to compare investments (with the same principal) when it isn’t clear which one yields more interest.

EXAMPLE

You have a choice between two investments for the next year:
  • Investment A pays an annual interest rate of 7.15%, compounded quarterly.
  • Investment B pays an annual interest rate of 7.1%, compounded continuously.
Assuming that the same principal would be used in each investment, which one yields more yearly interest?

We find the APY for each investment.

Investment A Investment B
7.15%, compounded quarterly
r = 0.0715, n = 4 		7.1%, compounded continuously
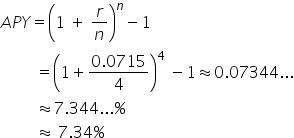
A P Y equals open parentheses 1 space plus space r over n close parentheses to the power of n minus 1 space space space space space space space space space equals open parentheses 1 plus fraction numerator 0.0715 over denominator 4 end fraction close parentheses to the power of 4 space minus 1 almost equal to 0.07344... space space space space space space space space space almost equal to 7.344... 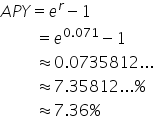percent sign space space space space space space space space space almost equal to space 7.34 percent sign A P Y equals e to the power of r minus 1 space space space space space space space space space equals e to the power of 0.071 end exponent minus 1 space space space space space space space space space almost equal to 0.0735812... space space space space space space space space space almost equal to 7.35812... percent sign space space space space space space space space space almost equal to 7.36 percent sign

Therefore, the investment that compounds continuously has the higher APY, which means it would earn more interest each year. While it might not be much interest in the first year, if the money were invested for several years, there would be sizeable differences in the interest each investment earns.

summary
In this lesson, you learned about annual percentage yield (APY) and how it is applied to investments with interest that is compounded a prescribed number (n) of times per year as well as compounded continuously. APY is a useful tool to tell how well an investment is doing in terms of the interest that it earns and can be used to compare investments.

Best of luck in your learning!

Source: THIS TUTORIAL WAS AUTHORED BY SOPHIA LEARNING. PLEASE SEE OUR TERMS OF USE.

Formulas to Know
APY for an Investment in Which Interest Is Compounded Continuously

A P Y space equals space e to the power of r minus 1, where r = the annual interest rate (in decimal form). To convert this to a percent, multiply by 100.

APY for an Investment in Which Interest Is Compounded n Times Per Year

A P Y space equals space open parentheses 1 plus r over n close parentheses to the power of n minus 1, where r = the annual interest rate (in decimal form) and n = the number of compounding periods in one year. To convert this to a percent, multiply by 100.

Annual Percentage Yield (APY)

A P Y space equals space fraction numerator I n t e r e s t space E a r n e d space i n space O n e space Y e a r over denominator P r i n c i p a l end fraction. space To convert this to a percentage, multiply by 100.

Interest Earned

I = A - P, where A is the amount in the account after a given length of time, and P is the principal (amount invested).

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.