Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Angles in Standard Position

Author: Sophia
PDF Version

what's covered
In this lesson, you will be introduced to angles and their measures. Specifically, this lesson will cover:

Table of Contents

1. Drawing Angles in Standard Position

1a. The Basics of Angles

Angles are virtually everywhere in the world around us. When an airplane takes off, it does so at some angle with the horizontal. When a golfer wishes to hit a golf ball out of a sand trap, they need to determine the best angle to do so.

Given your exposure to angles before taking this course, we need to look at a more specific way to define angles, which is standard position. Before doing so, we need to define some terms.

A ray consists of the endpoint of a line and all points extending in one direction from the endpoint. An angle is the figure formed by two rays with a common endpoint, called the vertex.

When constructing an angle, start with two rays, both pointing in the same direction. Leave one ray fixed, and rotate the other. The fixed ray is called the initial side, and the rotated side is called the terminal side. To indicate the direction of the rotation, an arrow is used as follows.

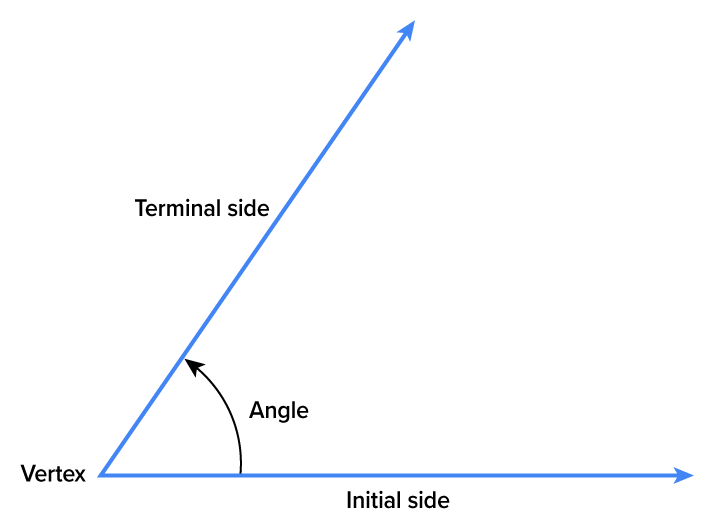
Two lines with arrows originating from the same point labeled ‘Vertex’. One line extends horizontally to the right, labeled ‘Initial side’, and the other extends diagonally, labeled ‘Terminal side’. A curved arrow between the two lines, starting from the initial side and pointing toward the terminal side, indicates the direction of rotation and is labeled ‘Angle’. 





In order to properly use angles, we have to know how to measure them. An angle measure is the amount of rotation from the initial side to the terminal side.



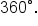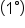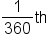Recall that one full circular rotation measures 360 degree. Then, one degree open parentheses 1 degree close parentheses is 1 over 360 th of a full rotation. It is very important to write the degree symbol when referencing the degree measure of an angle. For example, a 30-degree angle is written as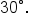 30 degree.
















terms to know






Standard Position


An angle that has its vertex at the origin and its initial side extended along the positive x-axis. 


Ray


Consists of the endpoint of a line and all points extending in one direction from the endpoint.


Angle


The figure formed by two rays with a common endpoint, called the vertex.


Angle Measure


The amount of rotation from the initial side to the terminal side.










1b. Angles in Standard Position






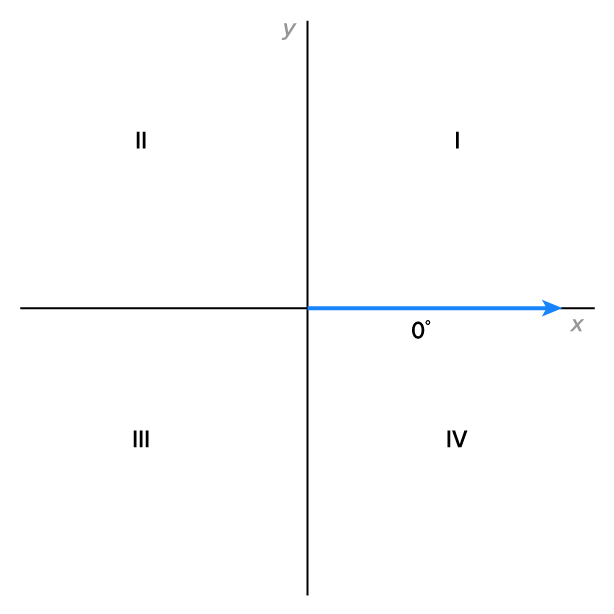
To better visualize angles, we use the xy-plane, where angles are drawn in standard position. 



Greek letters are often used to represent angles. The most popular of these is 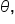theta comma which is pronounced “thay-ta” and spelled theta. An angle in standard position, labeled with the letter 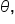theta comma is shown in the figure. 



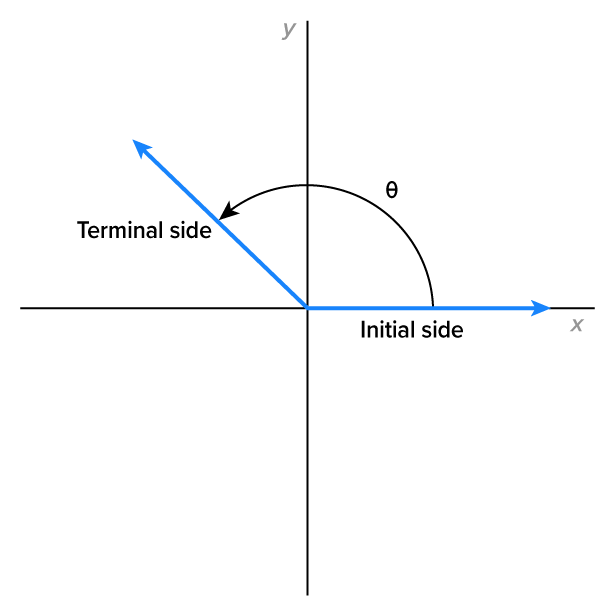
A graph with an x-axis and a y-axis. Two lines with arrows extend from the origin. One line labeled ‘Terminal side’ extends diagonally to the left in the second quadrant, and the other labeled ‘Initial side’ extends horizontally to the right along the positive x-axis. The angle between the two lines is marked as ‘θ’. A curved arrow between the two lines, starting from the initial side and pointing toward the terminal side, indicates the direction of rotation and the angle θ.







An angle can be positive, negative, or zero:





    

  • 
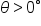theta greater than 0 degree when the rotation is counterclockwise from the initial side to the terminal side. 
    • 

  • 
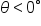theta less than 0 degree when the rotation is clockwise from the initial side to the terminal side. 
    • 

  • 
theta equals 0 degree when there is no rotation between the initial side and the terminal side. 
    • 


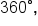For the time being, angles between short dash 360 degree and 360 degree comma inclusive, are considered.



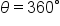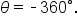
Shown below are the sketches of theta equals 360 degree and theta equals short dash 360 degree.







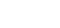
bold italic theta bold equals bold 360 bold degree


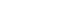
bold italic theta bold equals bold short dash bold 360 bold degree






A graph with an x-axis and a y-axis. A curved arrow starts from the positive x-axis, circles around the origin with a counterclockwise rotation, and ends just below the x-axis, representing a full rotation of 360 degrees.











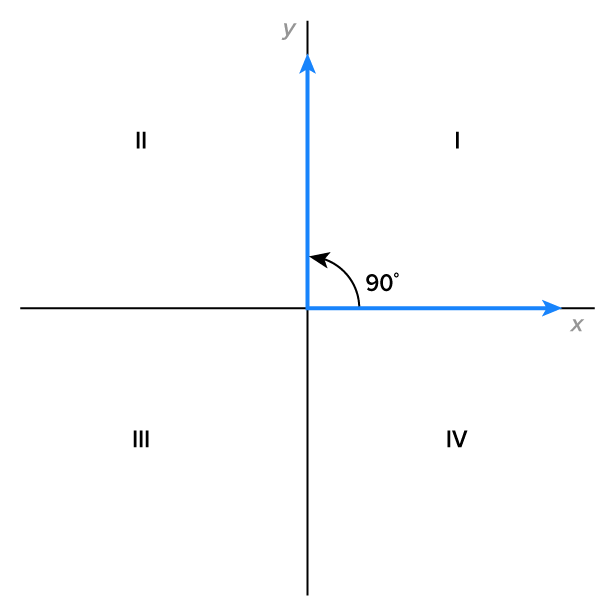
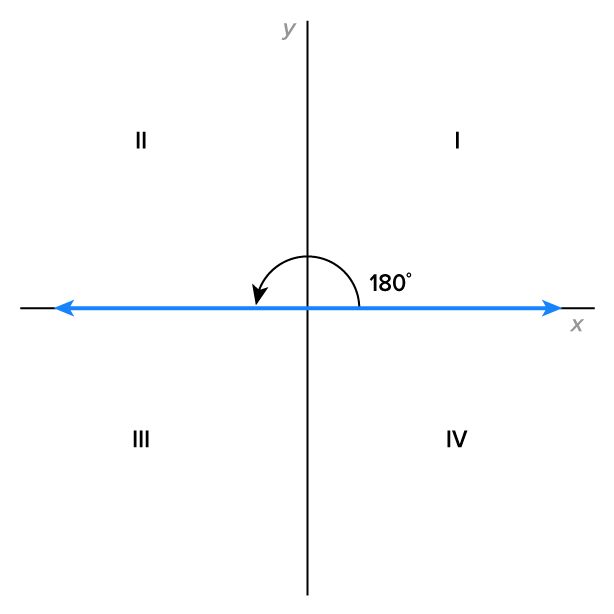
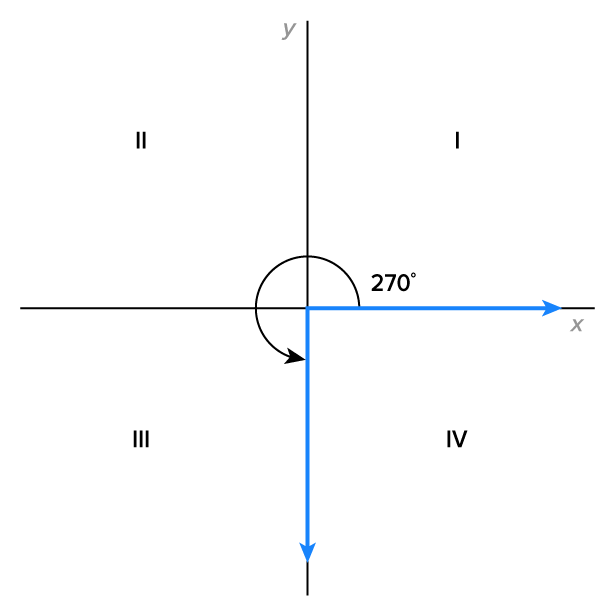
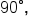
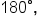
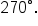
The angles below are the most recognizable in standard position since their terminal sides are one of the axes. These angles are called quadrantal angles. Note their measures: 0 degree comma 90 degree comma 180 degree comma 270 degree.







bold 0 bold degree


bold 90 bold degree






A graph with an x-axis and a y-axis. The quadrants are labeled with Roman numerals ‘1’, ‘2’, ‘3’, and ‘4’, each representing one quadrant. The quadrant marked '1' is the upper right, then 2 for the upper right, then 3 for the lower left, then 4 for the lower right. A line with an arrow, or a ray, extends from the origin, representing both the initial and terminal sides along the positive x-axis and representing the angle 0 degrees.


A graph with an x-axis and a y-axis. The quadrants are labeled with Roman numerals ‘1’, ‘2’, ‘3’, and ‘4’, each representing one quadrant. The quadrant marked '1' is the upper right, then 2 for the upper right, then 3 for the lower left, then 4 for the lower right. A line with an arrow, or a ray, extends from the origin, representing both the initial and terminal sides along the positive x-axis and representing the angle 0 degrees. A curved arrow starting from the initial side and pointing toward the terminal side is marked between the lines, indicating an angle of 90 degrees and a counterclockwise rotation.






bold 180 bold degree


bold 270 bold degree






A graph with an x-axis and a y-axis. The quadrants are labeled with Roman numerals ‘1', ‘2’, ‘3,’ and ‘4’, each representing one quadrant. Two with arrows extends horizontally through the origin, along the x-axis. The initial side extends along the positive x-axis, and the terminal side extends along the negative x-axis. A curved arrow starting from the initial side and pointing toward the terminal side indicates an angle of 180 degrees and a counterclockwise rotation.


A graph with an x-axis and a y-axis. The quadrants are labeled with Roman numerals ‘1’, ‘2’, ‘3’, and ‘4’, each representing one quadrant. The quadrant marked '1' is the upper right, then 2 for the upper right, then 3 for the lower left, then 4 for the lower right. A line with an arrow, or a ray, extends from the origin, representing both the initial and terminal sides along the positive x-axis and representing the angle 0 degrees. Clockwise rotation begins from the positive x-axis and ends at the negative y-axis, indicating an angle of 270 degrees.





















hint





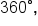Notice that the angles 0 degree comma 360 degree comma and short dash 360 degree all have the same initial and terminal sides. This is a big idea coming up later!


 




A quadrantal angle’s terminal side coincides with the x- or y-axis. 



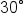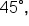The quadrantal angles can be referenced in order to sketch other angles. When an angle is a multiple of 30 degree or 45 degree comma we can more easily visualize the angle as a fraction of a full rotation. 



For example, we know that 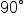90 degree is a quarter of a full rotation since 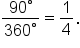fraction numerator 90 degree over denominator 360 degree end fraction equals 1 fourth. This means that using the initial side along the positive x-axis, rotate counterclockwise until reaching the positive y-axis. This angle is 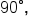90 degree comma as shown in the picture above. 







EXAMPLE

Sketch the angle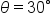 theta equals 30 degree in standard position. 



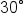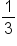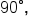Since 30 degree is 1 third of 90 degree comma this means that the rotation is 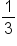1 third the size of the rotation for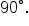 90 degree.



Consider this picture, which shows the right angle split into three equal angles: 



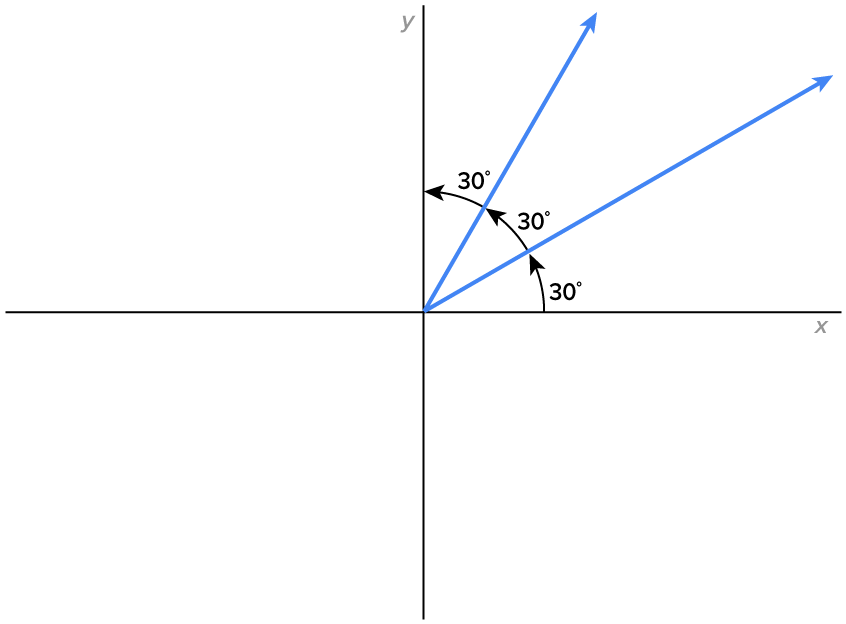
A graph with an x-axis and a y-axis. Two lines with arrows extend diagonally from the origin into the first quadrant, dividing the quadrant into three equal segments, each with an angle of 30 degrees. Three curved arrows indicate counterclockwise rotation: the first from the positive x-axis to the first line, the second from the first line to the second line, and the third from the second line to the positive y-axis, each representing a 30 degree angle. 



This means that the sketch of the angle theta equals 30 degree in standard position is: 



A graph with an x-axis and a y-axis representing the angle theta of 30 degrees in standard position. The angle has its vertex at the origin. Two lines with arrows originate from the origin, where one line extends along the positive x-axis, representing the initial side, and the other line extends diagonally into the first quadrant, representing the terminal side. A curved arrow, from the initial side toward the terminal side with a counterclockwise rotation, represents the angle 30 degrees.




















watch





In this video, we’ll sketch the angle theta equals short dash 120 degree in standard position.














 


Here are a few more examples of angles drawn in standard position. 






Angles Drawn in Standard Position





A graph with an x-axis and a y-axis representing the angle 135 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends diagonally to the left into the second quadrant, representing the terminal side. The angle between the two sides is marked as 135 degrees. A curved arrow from the initial to the terminal side with a counterclockwise rotation represents the angle 135 degrees.


A graph with an x-axis and a y-axis representing the angle −60 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends downward diagonally into the fourth quadrant, representing the terminal side. The angle between the two sides is marked as −60 degrees. A curved arrow from the initial to the terminal side with a clockwise rotation represents the angle −60 degrees.


A graph with an x-axis and a y-axis representing the angle −225 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends diagonally to the left into the second quadrant, representing the terminal side. A curved arrow from the initial side to the terminal side with a clockwise rotation represents the angle −225 degrees.





















try it





Consider the angle sketched in standard position. 

A graph with an x-axis and a y-axis intersecting at the origin. A line with arrows on both ends extends from the negative x-axis to the positive x-axis, passing through the origin. A curved arrow extends below the x-axis, showing a clockwise rotation from the positive x-axis to the negative x-axis, forming an angle labeled ‘Theta (θ)’. 




What is the measure of the angle?

short dash 180 degree


























try it





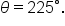
Consider the angle theta equals 225 degree. 




Sketch the angle in standard position.

A graph with an x-axis and a y-axis representing the angle theta of 225 degrees in standard position. The angle has its vertex at the origin. Two lines with arrows extend from the origin, where one line extends along the positive x-axis, representing the initial side, and the other extends diagonally downward to the left into the third quadrant, representing the terminal side. A curved arrow above the x-axis, starting from the initial side toward the terminal side, indicates a counterclockwise rotation.


























term to know






Quadrantal Angle


An angle whose terminal side coincides with the x- or y-axis.



 










2. Finding Coterminal Angles






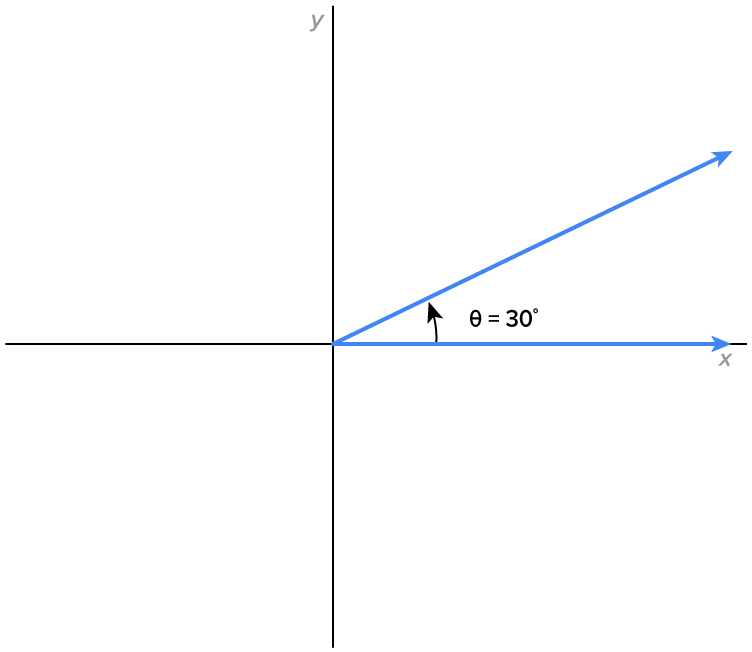
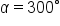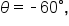Consider the angles alpha equals 300 degree and theta equals short dash 60 degree comma both in standard position, shown in the figure. 



A graph with the x-axis and y-axis representing the coterminal angles alpha of 300 degrees and theta of −60 degrees in the standard position. Both the angles have their vertex at the origin. Two lines with arrows extend from the origin, where one line extends along the positive x-axis, representing the initial side, and the other extends diagonally downward into the fourth quadrant, representing the terminal side. A curved arrow from the initial to the terminal side with a clockwise rotation represents the angle theta of −60 degrees. Another curved arrow from the initial side to the terminal side with a counterclockwise rotation represents the angle alpha of 300 degrees.







Notice how they both have the same terminal side. When two angles in standard position share the same terminal side, the angels are called coterminal. 



So far, we have only considered angles formed by rotating at most 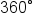360 degree in either direction. When the measure of an angle has absolute value more than 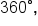360 degree comma it means that the ray is rotated more than one full rotation from its initial side. 



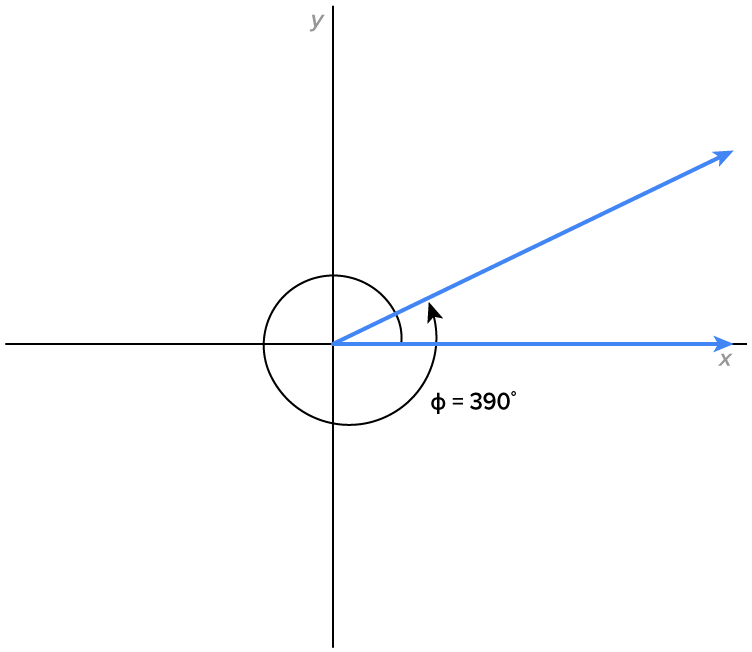
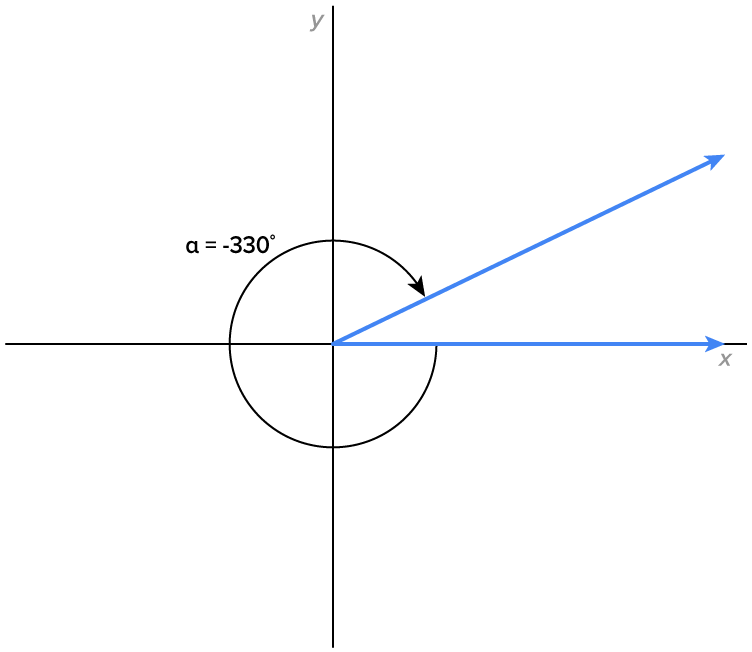
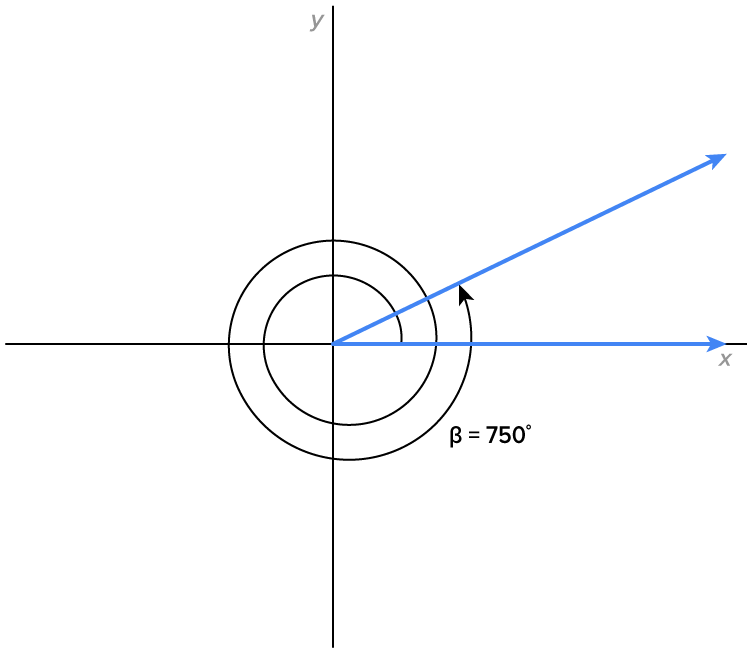
Consider the angles given below, which all share the same terminal side. 



Note: 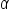alpha is the Greek letter alpha, 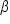beta is the Greek letter beta, and 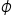ϕ is the Greek letter phi, pronounced “fee.” 







bold italic theta bold equals bold 30 bold degree


bold italic ϕ bold equals bold 390 bold degree






A graph with an x-axis and a y-axis representing the angle θ (theta) equals 30 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends diagonally into the first quadrant, representing the terminal side. A curved arrow circles the origin in a counterclockwise rotation. It starts from the initial side and ends at the terminal side, representing the angle theta equals 30 degrees.


A graph with an x-axis and a y-axis representing the angle φ (phi) equals 390 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends diagonally into the first quadrant, representing the terminal side. A curved arrow circles the origin in a counterclockwise rotation. It starts from the initial side, passes through all the axes, and ends at the terminal side, representing the angle phi equals 390 degrees.






bold italic alpha bold equals bold short dash bold 330 bold degree


bold italic beta bold equals bold 750 bold degree






A graph with an x-axis and a y-axis representing the angle α equals −330 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends diagonally into the first quadrant, representing the terminal side. A curved arrow circles the origin in a clockwise rotation beginning at the initial side and ending at the terminal side, representing the angle α equals −330 degrees.


A graph with an x-axis and a y-axis representing the angle β equals 750 degrees in standard position. Two lines with arrows extend from the origin. One line extends along the positive x-axis, representing the initial side, and the other extends diagonally into the first quadrant, representing the terminal side. A curved arrow circles the origin twice in a counterclockwise rotation. The curved arrow starts from the initial side, passes through all the axes twice, and ends at the terminal side, representing the angle β equals 750 degrees.








All four of these angles are coterminal since they share the same terminal side. 



Considering the angle 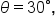theta equals 30 degree comma notice the following: 





    

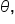  • Starting at the terminal side of theta comma applying one full counterclockwise rotation to get angle 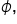ϕ comma which has measure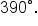 390 degree.

    • 

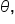  • Starting at the terminal side of theta comma applying one full clockwise rotations to get angle 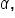alpha comma which has measure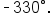 short dash 330 degree.

    • 

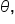  • Starting at the terminal side of theta comma applying two full counterclockwise rotations to get angle 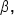beta comma which has measure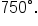 750 degree.

    • 


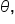In fact, to find an angle coterminal to a given angle theta comma add any multiple of 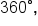360 degree comma which is one full rotation, to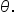 theta.
















try it





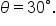
Consider the angle theta equals 30 degree.




What is the measure of the angle obtained after applying three full counterclockwise rotations to θ?

Each counterclockwise rotation is 360°. Therefore, the measure of the angle is 30 degree plus 3 open parentheses 360 degree close parentheses equals 1110 degree.











What is the measure of the angle obtained after applying four full clockwise rotations to θ?

Each clockwise rotation is -360°. Therefore, the measure of the angle is 30 degree plus 4 open parentheses short dash 360 degree close parentheses equals short dash 1410 degree.








 





Thus, when the terminal ray is rotated by any multiple of 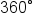360 degree counterclockwise or clockwise, the resulting angle has the same terminal side. This means that the measures of two coterminal angles differ by a multiple of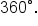 360 degree.



This gives a general rule for finding coterminal angles. 
















formula to know






Finding Coterminal Angles


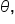Given an angle theta comma adding or subtracting any integer multiple of 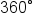360 degree results in an angle coterminal to 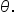theta. That is, if k is an integer, then 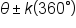theta plus-or-minus k open parentheses 360 degree close parentheses is coterminal to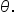 theta.













EXAMPLE

Find two angles, one positive and one negative, that are coterminal to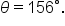 theta equals 156 degree.



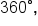While you could add or subtract any multiples of 360 degree comma we’ll add and subtract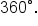 360 degree.






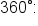
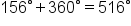
Add 360 degree colon 156 degree plus 360 degree equals 516 degree



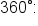
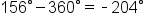
Subtract 360 degree colon 156 degree minus 360 degree equals short dash 204 degree






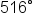Two coterminal angles are 516 degree and short dash 204 degree.







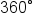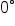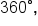In many applications, angles that are either negative or more than 360 degree can be awkward to work with. As a result of the relationship we established between coterminal angles, every angle is coterminal with an angle between 0 degree and 360 degree comma which we will find is the most convenient range of values to use. 



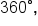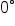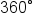Thus, given a negative angle or an angle larger than 360 degree comma we can find a coterminal angle between 0 degree and 360 degree as follows: 




    

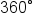  • If the angle is negative, add 360 degree to the angle. If the angle is positive, you are done. If it is negative, continue to add 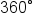360 degree until the result is positive. 
    • 

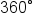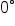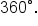
  • If the angle is positive, subtract 360 degree until the result is an angle between 0 degree and 360 degree.

    • 





EXAMPLE

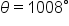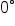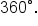
Find an angle coterminal to theta equals 1008 degree that is between 0 degree and 360 degree.



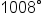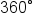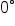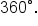
Since 1008 degree is positive, subtract 360 degree until we get a number between 0 degree and 360 degree.




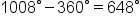
1008 degree minus 360 degree equals 648 degree



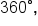This is larger than 360 degree comma so keep subtracting. 




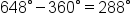
648 degree minus 360 degree equals 288 degree



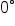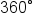This is between 0 degree and 360 degree; stop here. 



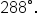
Thus, the requested coterminal angle is 288 degree.




















try it





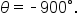
Consider the angle theta equals short dash 900 degree. 




Find an angle coterminal to the given angle that is between 0° and 360°.

To find the angle, add 360° until obtaining an angle between 0° and 360°.  






short dash 900 degree plus 360 degree equals short dash 540 degree


short dash 540 degree plus 360 degree equals short dash 180 degree


short dash 180 degree plus 360 degree equals 180 degree




 
Therefore, the coterminal angle is 180°.

























hint





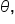When given an angle theta and you wish to find another angle coterminal to theta comma add or subtract 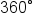360 degree to theta until getting an angle in the desired range.











EXAMPLE

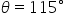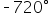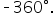
Find an angle coterminal to theta equals 115 degree that is between short dash 720 degree and short dash 360 degree.



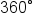Since the desired range is between two negative angles, we subtract 360 degree until our angle falls into that range.  








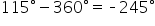
115 degree minus 360 degree equals short dash 245 degree


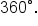Subtract 360 degree. Note the result is not in our desired range, so we will subtract again in the next step.






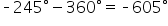
short dash 245 degree minus 360 degree equals short dash 605 degree


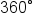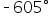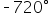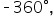Subtract 360 degree again. This time, short dash 605 degree is between short dash 720 degree and short dash 360 degree comma so we have found our coterminal angle.




 


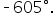
The coterminal angle is short dash 605 degree.




















term to know






Coterminal Angles


Angles that share the same terminal side.



 














summary






In this lesson, you learned about drawing an angle in standard position, which means that its initial side (the fixed ray) is along the positive x-axis, vertex is at the origin, and the terminal side is rotated in a counterclockwise or clockwise direction. 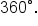You covered some additional basics of angles, recalling that an angle measure is the amount of rotation from the initial side to the terminal side, and that one full circular rotation measures 360 degree. You also learned that we draw angles in standard position on the xy-plane, and angles are often represented by the Greek letter theta. Depending on the direction of the rotation from the initial side to the terminal side, an angle can be positive (counterclockwise rotation), negative (clockwise rotation), or zero (no rotation). 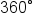Finally, you learned that two angles in standard position which share the same terminal side are called coterminal; to find a coterminal angle, add or subtract an integer multiple of 360 degree to the given angle. 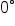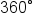This is especially useful to find an angle between 0 degree and 360 degree that is coterminal to an angle that is either negative or larger than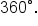 360 degree.




 


SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM OPENSTAX "PRECALCULUS” BY JAY ABRAMSON. ACCESS FOR FREE AT OPENSTAX.ORG/DETAILS/BOOKS/PRECALCULUS-2E. LICENSE: CREATIVE COMMONS ATTRIBUTION 4.0 INTERNATIONAL.



















Terms to Know









Angle





The figure formed by two rays with a common endpoint, called the vertex.





Angle Measure





The amount of rotation from the initial side to the terminal side.





Coterminal Angles





Angles that have the same initial and terminal side.





Quadrantal Angle





An angle whose terminal side coincides with the x or y-axis.





Ray





Consists of the endpoint of a line and all points extending in one direction from the endpoint.





Standard Position





An angle that has its vertex at the origin and its initial side extended along the positive x-axis.



















Formulas to Know









Finding Coterminal Angles





Given an angle theta comma adding or subtracting any integer multiple of 360 degree results in an angle coterminal to theta. That is, if k is an integer, then theta plus-or-minus k open parentheses 360 degree close parentheses is coterminal to theta.
































© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.