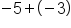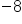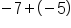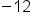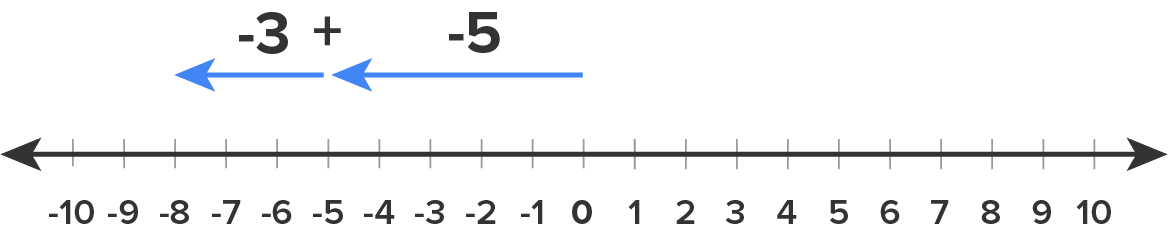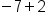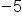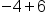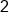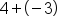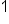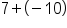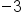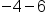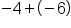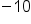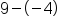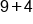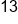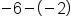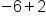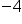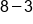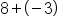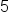Addition and Subtraction of Integers

1. Adding Integers

The ability to work comfortably with negative numbers is essential to success in math. For this reason, we will do a quick review of adding and subtracting positive and negative integers. If you remember from our last challenge, integers are positive and negative whole numbers and zero.

key concept

When adding integers, we have two cases to consider. The first case demonstrates a situation with matching signs: both integers are either positive, or both integers are negative. If the signs match, we will add the numbers together, and keep the sign. You are likely comfortable adding two positive numbers, so we’ll illustrate this using the following examples:

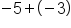
	Same sign, add 5 + 3, keep the negative.
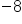
	Our Solution

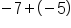
	Same sign, add 7 + 5, keep the negative.
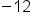
	Our Solution

IN CONTEXT

Think about the addition (or subtraction) of integers as making or spending money. If the value is positive, you’ve made money. If the value is negative, you have spent money. Let’s look at the example above again using this idea.

(-5) + (-3) This means you have spent $5 at one store and then spent an additional $3 at another store. How much money have you spent today? You’ve spent $8, or -8.

Still don’t quite get it? Let’s look at this another way. Think about the addition (or subtraction) of integers as a number line, or a thermometer. A negative value means you would move to the left to make the number smaller and a positive value means you would move to the right to make the number larger.

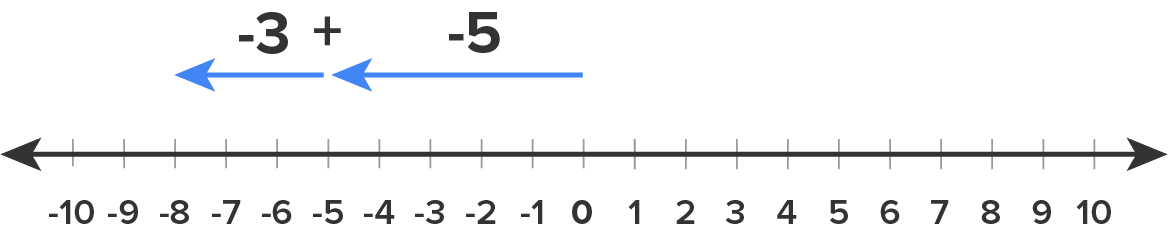
The second case, -7 + (-5), demonstrates a situation with signs that don't match (one integer is positive and one integer is negative). We will subtract the numbers (as if they were all positive), and then use the sign from the larger number. This means if the larger number is positive, the answer is positive; and if the larger number is negative, the answer is negative. This is shown in the following examples:

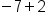
	Different signs, subtract 7 - 2, use sign from bigger number, negative.
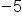
	Our Solution

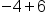
	Different signs, subtract 6 - 4, use sign from bigger number, positive.
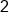
	Our Solution

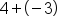
	Different signs, subtract 4 - 3, use sign from bigger number, positive.
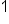
	Our Solution

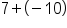
	Different signs, subtract 10 - 7, use sign from bigger number, negative.
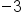
	Our Solution

IN CONTEXT

Using our money analogy, let’s look at the first couple examples.

You borrowed $7 from a friend and have paid back $2. How much money do you still owe your friend? You still owe your friend $5, or -5.

You borrowed $4 from a friend and have paid back $6. How much money do you still owe your friend? In this case, you overpaid so they now owe you money. You overpaid by $2, or 2.

Using our number line strategy, let’s look at the first couple examples.

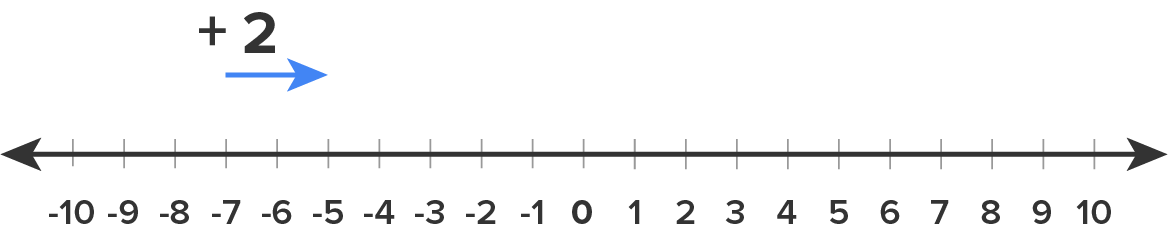
You started at -7 and because “2” is positive, you move two units to the right. You land on -5.

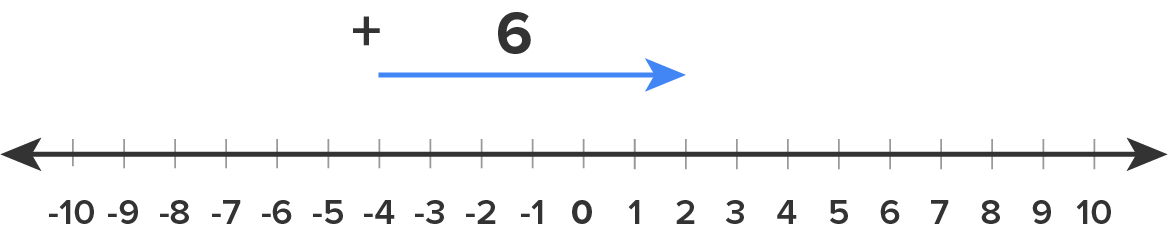
You started at -4 and because “6” is positive, you move six units to the right. You land on 2.

big idea

When adding two numbers with matching signs, add the two numbers (as if they are positive) and keep the sign. When adding two numbers with opposite signs, subtract the smaller number from the larger number (as if they are positive), and keep the sign of the larger number.

2. Subtracting Integers

For subtraction of negative numbers, you can either treat it like a subtraction problem, or you can change the problem to an addition problem, which can then be solved using the above methods. If you prefer to change the problem to an addition problem, you will need to switch the signs. Think about it like keeping the balance. To change subtraction to addition is to add the opposite of the number after the subtraction sign. Often this method is referred to "adding the opposite." This is illustrated in the following examples:

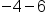
	Add the opposite of 6.
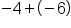
	Same sign, add 4 + 6, keep the negative.
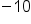
	Our Solution

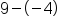
	Add the opposite of -4
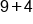
	Same sign, add 9 + 4, keep the positive.
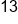
	Our Solution

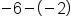
	Add the opposite of -2.
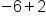
	Different sign, subtract 6 - 2, use sign from bigger number, negative.
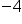
	Our Solution

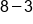
	Add the opposite of 3.
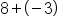
	Different signs, subtract 8 - 3, use sign from bigger number, positive.
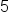
	Our Solution

IN CONTEXT

Using our money analogy, let’s look at the first couple examples.

-4 – 6 You owe (negative value) one friend $4 and then you need to borrow an additional $6. How much money do you owe your friend now? You took out two debts to a total of $10, or -10.

9 – (-4) You have $9 and a friend took away (subtract) a debt (negative value) of $4 that they owed you. How much money do you have now? Since your friend paid you back their debt, you have now added to your bank account, that’s now a positive value, so $9 + $4 = $13, or 13.

Using our number line strategy, let’s look at the first couple examples.

You started at -4 and because “6” is negative (or you’re adding a negative), you move six units to the left. You land on -10.


You started at 9 and because you subtract a negative (or add) “4”, you move nine units to the right. You land on 2.