Table of Contents |
The ability to work comfortably with negative numbers is essential for success in algebra. For this reason, we will do a quick review of adding and subtracting positive and negative integers. Integers are all the positive whole numbers, zero, and their opposites (negative numbers).
Before we go directly into the rules for adding integers, consider this situation:
A friend gives you 8 chocolate bars, then gives you 4 more. This means your friend gave you 12 chocolate bars 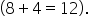
Another way to look at this situation is from your friend's perspective, meaning they lost 8 chocolate bars, then they lost 4 more. Using negative numbers to represent the losses, “-8” can be used to represent the first loss, “-4” can be used to represent the second loss, and “-12” can be used to represent the total loss.
This means we can also write 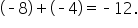
This is illustrated in the following examples:
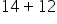
|
Same sign; just add. |

|
Our solution |
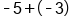
|
Same sign; add 5 + 3 and keep the negative. |
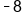
|
Our solution |
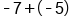
|
Same sign; add 7 + 5 and keep the negative. |
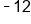
|
Our solution |
Now let’s imagine a scenario where you spent $10 on lottery tickets, but you won $3 back.
You lost $10 and got $3 back, which means overall, you lost $7. This is written 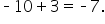
The store gained $10 but then lost $3, which means overall, they gained $7. This is written 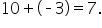
This is shown in the following examples:
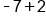
|
Different signs; subtract 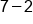 and use sign from bigger number (negative). and use sign from bigger number (negative).
|
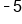
|
Our solution |
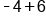
|
Different signs; subtract 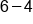 and use sign from bigger number (positive). and use sign from bigger number (positive).
|
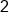
|
Our solution |
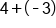
|
Different signs; subtract 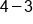 and use sign from bigger number (positive). and use sign from bigger number (positive).
|
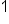
|
Our solution |
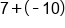
|
Different signs; subtract 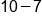 and use sign from bigger number (negative). and use sign from bigger number (negative).
|

|
Our solution |
Consider a situation where you have $12 in your pocket but had to spend $8 for lunch. How much is left? We can look at this problem using two representations.
| Mathematical Representation | Explanation |
|---|---|
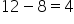
|
You started with $12, then spent $8, leaving you with $4. |
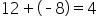
|
You started with $12, then added a loss of $8, leaving you with $4. |
This is illustrated in the following examples:
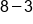
|
Add the opposite of 3. |
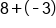
|
Different signs; subtract 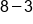 and use sign from bigger number (negative). and use sign from bigger number (negative).
|
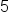
|
Our solution |
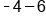
|
Add the opposite of 6. |
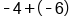
|
Same sign; add 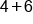 and keep the negative. and keep the negative.
|
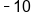
|
Our solution |
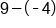
|
Add the opposite of -4. |
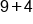
|
Same sign; add 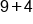 and keep the positive. and keep the positive.
|
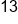
|
Our solution |
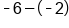
|
Add the opposite of -2. |
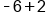
|
Different signs; subtract 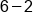 and use sign from bigger number (negative). and use sign from bigger number (negative).
|
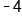
|
Our solution |
Source: THIS TUTORIAL HAS BEEN ADAPTED FROM "BEGINNING AND INTERMEDIATE ALGEBRA" BY TYLER WALLACE. ACCESS FOR FREE AT www.wallace.ccfaculty.org/book/book.html. License: Creative Commons Attribution 3.0 Unported License