Use Sophia to knock out your gen-ed requirements quickly and affordably. Learn more
Become a Member Try for Free
×

Absolute Value Functions

Author: Sophia
PDF Version

what's covered
In this lesson, you will learn about absolute value functions. Specifically, this lesson will cover:

Table of Contents

1. The Absolute Value Function

1a. The Piecewise Definition of Absolute Value

Recall that 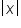open vertical bar x close vertical bar means “the absolute value of x”, which represents the distance that a number x is from 0 (on the number line).

Consider the number line shown below, with the numbers 3 and -6 marked.

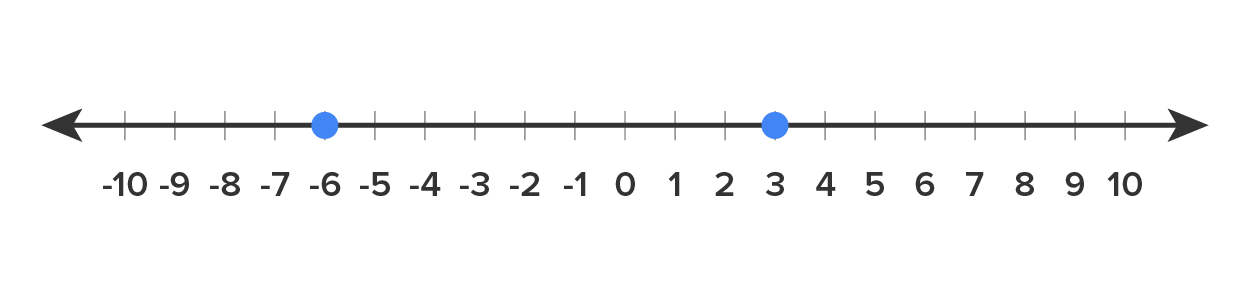
A numbered line divided into units ranging from −10 to 10 with marked points at −6 and 3.

Since the number 3 is a distance of 3 units from 0, we say that 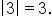open vertical bar 3 close vertical bar equals 3.

Since the number -6 is a distance of 6 units from 0, we say that 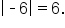open vertical bar short dash 6 close vertical bar equals 6.

In general, evaluating 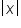open vertical bar x close vertical bar requires two different rules, depending on what x is.

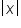  • If x is nonnegative, then open vertical bar x close vertical bar and x are the same.
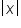  • If x is negative, then open vertical bar x close vertical bar is the opposite of x (turning a negative into a positive).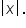
This leads to the piecewise definition for open vertical bar x close vertical bar.

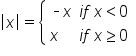
open vertical bar x close vertical bar equals open curly brackets table attributes columnalign left center end attributes row cell short dash x end cell cell i f space x less than 0 end cell row x cell i f space x greater or equal than 0 end cell end table close

term to know
Absolute Value
The distance that a number is from 0 on the number line.

1b. The Graph of the Basic Absolute Value Function

In the table below, you see several input-output pairs for 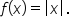f open parentheses x close parentheses equals open vertical bar x close vertical bar.

bold italic x -5 -4 -3 -2 -1 0 1 2 3 4 5
bold italic f open parentheses bold x close parentheses bold equals open vertical bar bold x close vertical bar 5 4 3 2 1 0 1 2 3 4 5

Here is the resulting graph:

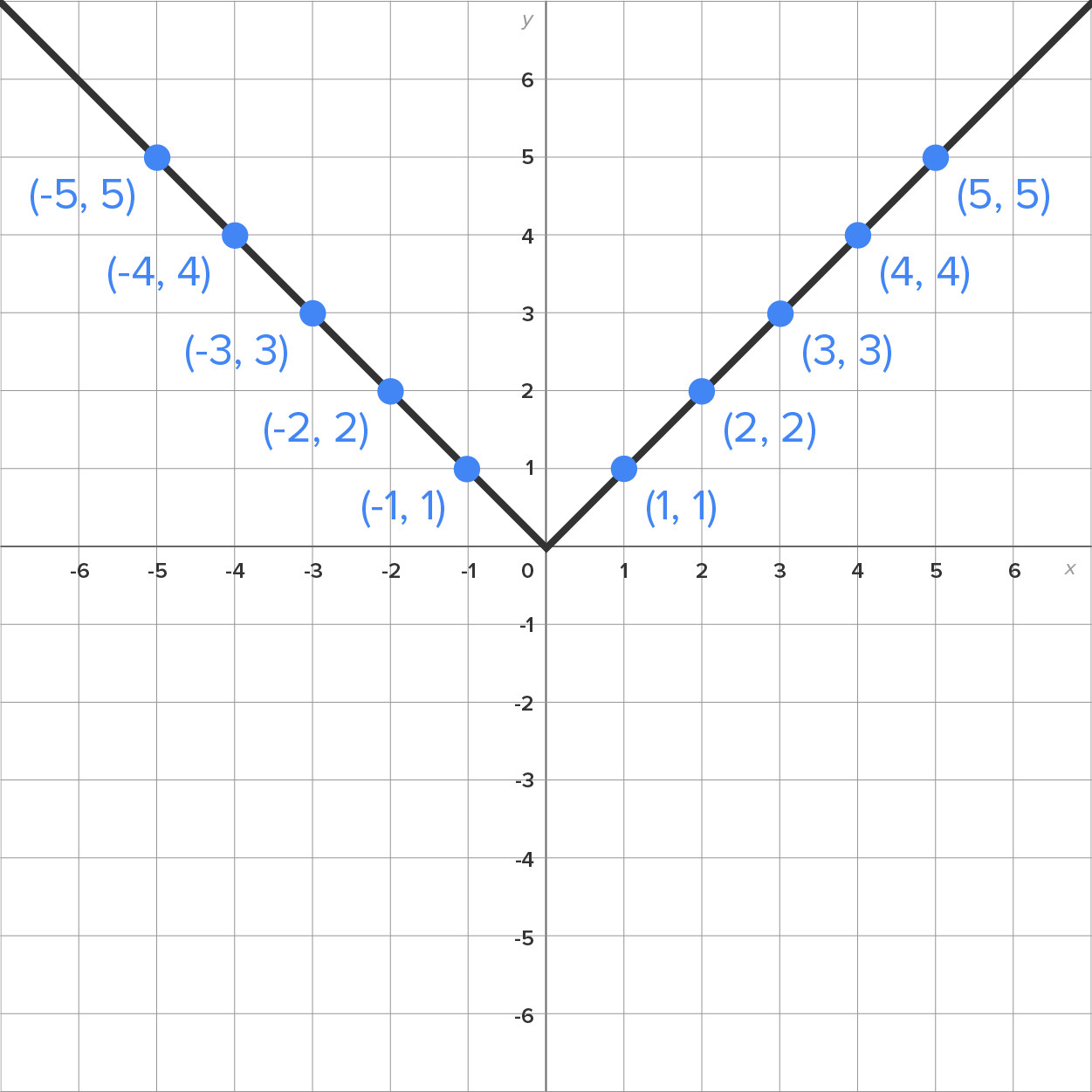
A graph with an x-axis and a y-axis ranging from −6 to 6 and intersecting at the origin. A line slants downward from left to right in the second quadrant, intersecting at the origin, and then slants upward from the origin in the first quadrant, forming a V-shaped absolute value function. There are several points marked along the line, which are labeled (−5, 5), (−4, 4), (−3, 3), (−2, 2), (−1, 1), (1, 1), (2, 2), (3, 3), (4, 4), and (5, 5).

2. Graphing Absolute Value Functions

2a. Shifting, Stretching, and Reflecting the Basic Absolute Value Function

From what you learned in the “Shifting and Stretching Graphs” section, you can apply these rules to the absolute value function.

Function Graph Shifts and/or Stretches from bold italic f open parentheses bold x close parentheses bold equals open vertical bar bold x close vertical bar
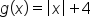
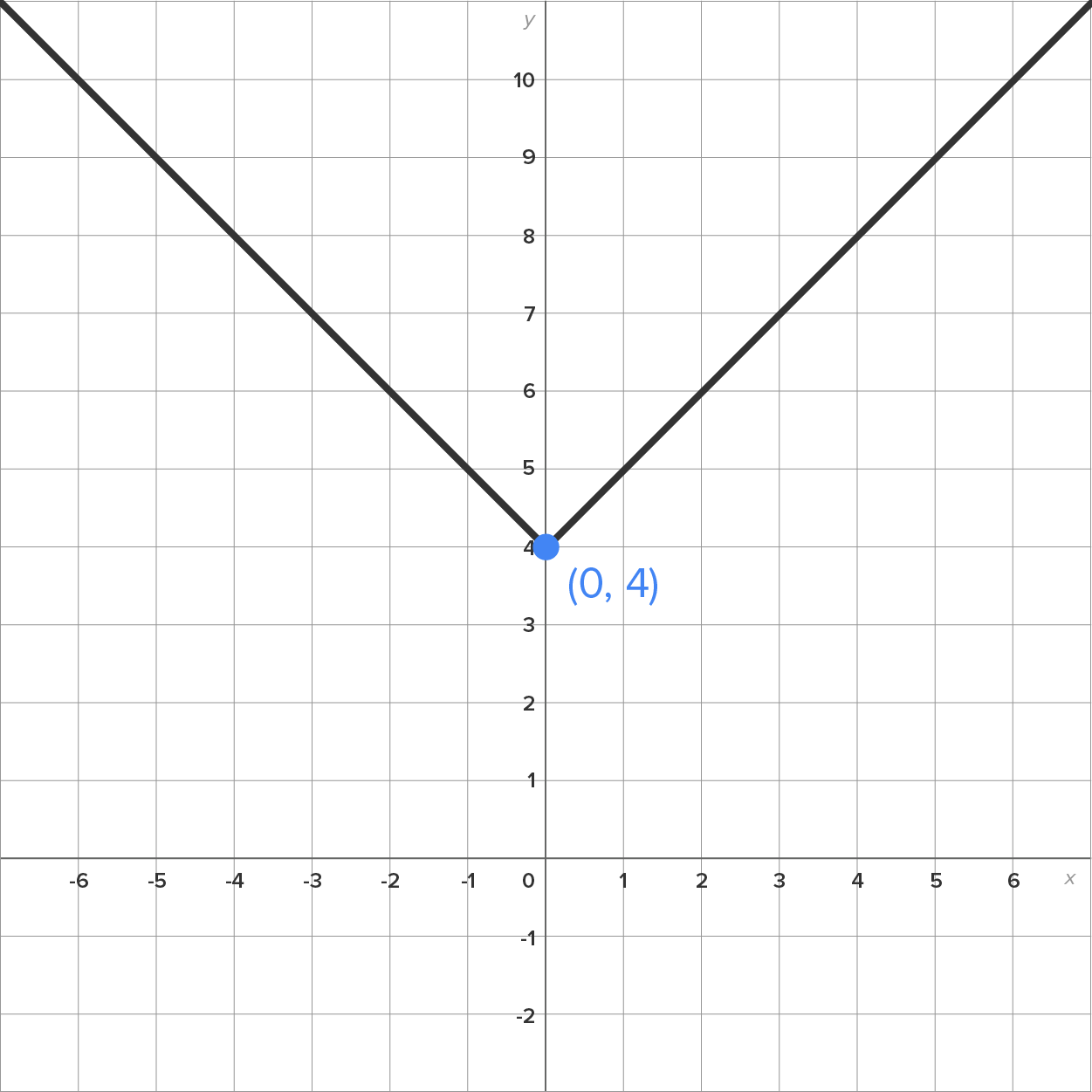
g open parentheses x close parentheses equals open vertical bar x close vertical bar plus 4 A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −2 to 10 intersecting at the origin. A line slants downward from left to right in the second quadrant, intersecting at the marked point labeled (0, 4), and slants upward from this point to the first quadrant, forming a V-shaped absolute value function. Up 4 units
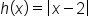
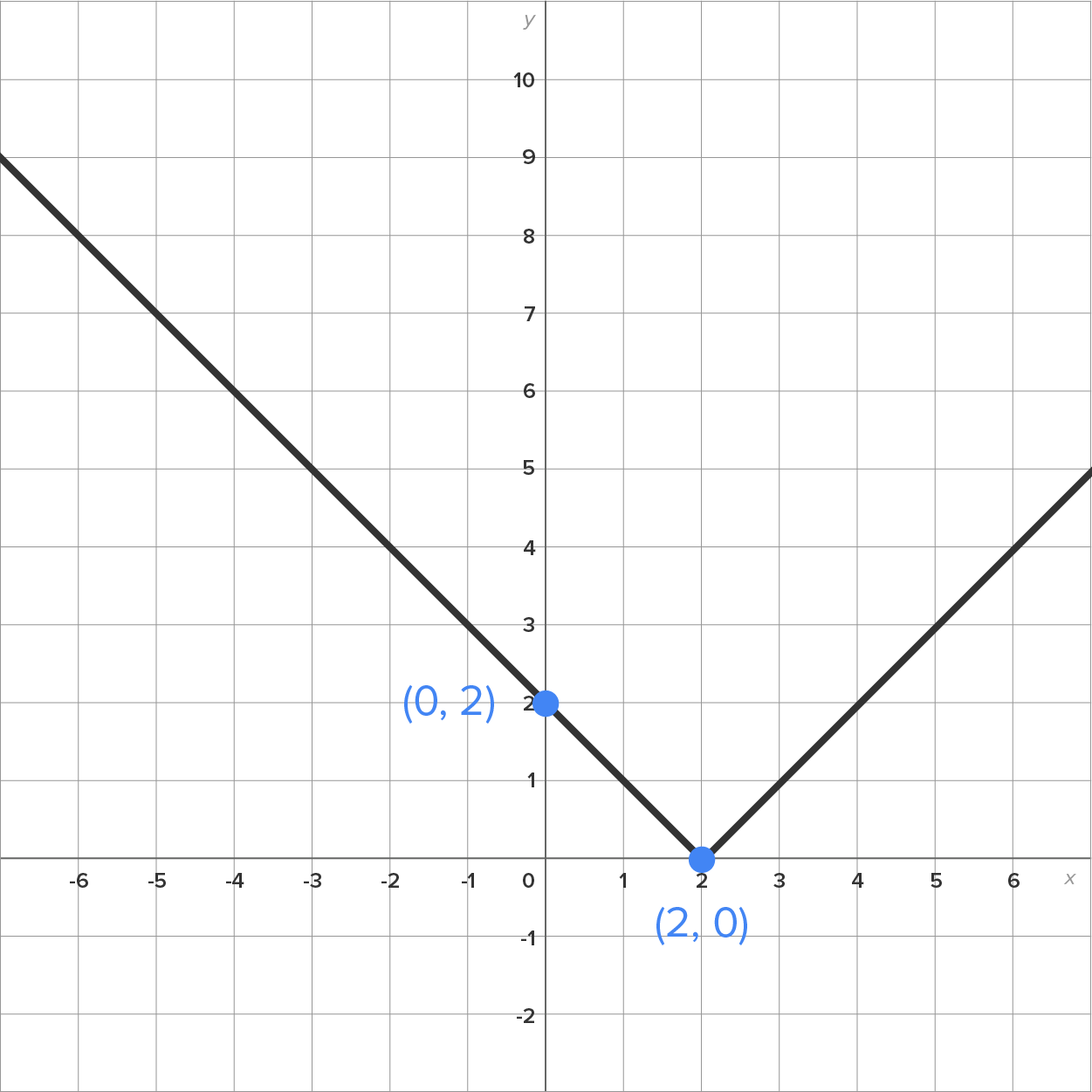
h open parentheses x close parentheses equals open vertical bar x minus 2 close vertical bar A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −2 to 10 intersecting at the origin. A line slants downward from left to right from the second quadrant, passing through the marked point (0, 2) and then extends to the first quadrant to connect to a marked point (2, 0). The line slants upward from this point, forming a V-shaped absolute value function. Right 2 units
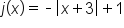
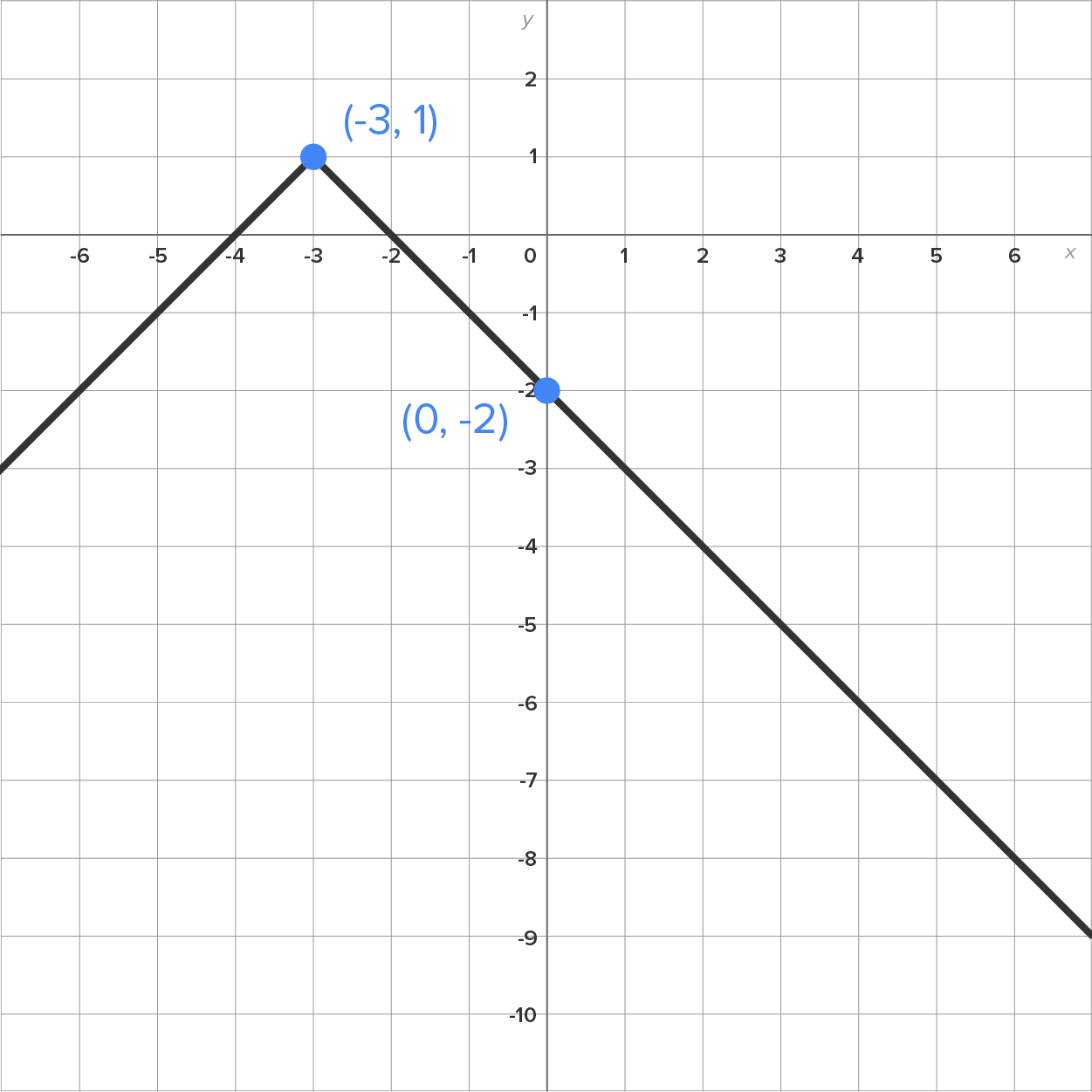
j open parentheses x close parentheses equals short dash open vertical bar x plus 3 close vertical bar plus 1 A graph with an x-axis ranging from −6 to 6 and a y-axis ranging from −10 to 2 intersecting at the origin. A line slants upward from the third quadrant, rests at the marked point (−3, 1), then slants downward from this point, passes through the y-axis at (0, −2), and extends into the fourth quadrant, forming an upside-down V-shaped absolute value function. Left 3 units, reflected over the x-axis, then moved up 1 unit

2b. Other Absolute Value Graphs

The function 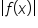open vertical bar f open parentheses x close parentheses close vertical bar can be written in piecewise form by replacing “x” with “f open parentheses x close parentheses.”

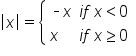
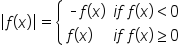
open vertical bar x close vertical bar equals open curly brackets table attributes columnalign left center end attributes row cell short dash x end cell cell i f space x less than 0 end cell row x cell i f space x greater or equal than 0 end cell end table close → open vertical bar f open parentheses x close parentheses close vertical bar equals open curly brackets table attributes columnalign left center end attributes row cell short dash f open parentheses x close parentheses end cell cell i f space f open parentheses x close parentheses less than 0 end cell row cell f open parentheses x close parentheses end cell cell i f space f open parentheses x close parentheses greater or equal than 0 end cell end table close

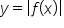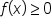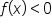We can adapt this idea to graph a function of the form y equals open vertical bar f open parentheses x close parentheses close vertical bar. In order to do this, think about what it means when we say f open parentheses x close parentheses greater or equal than 0 and f open parentheses x close parentheses less than 0.

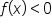If f open parentheses x close parentheses less than 0, this really means 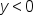y less than 0, indicating that the corresponding point on the graph is below the x-axis.

If 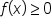f open parentheses x close parentheses greater or equal than 0, this really means 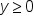y greater or equal than 0, indicating that the corresponding point on the graph is on or above the x-axis.

Recall from challenge 1.3.4 “Shifting and Stretching Graphs” that the graph of 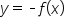y equals short dash f open parentheses x close parentheses reflects the graph of 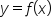y equals f open parentheses x close parentheses across the x-axis. Thus, if 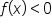f open parentheses x close parentheses less than 0, then the graph of 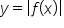y equals open vertical bar f open parentheses x close parentheses close vertical bar reflects over the x-axis (to the positive side). 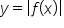Otherwise, the graphs of f open parentheses x close parentheses and y equals open vertical bar f open parentheses x close parentheses close vertical bar are the same.

EXAMPLE

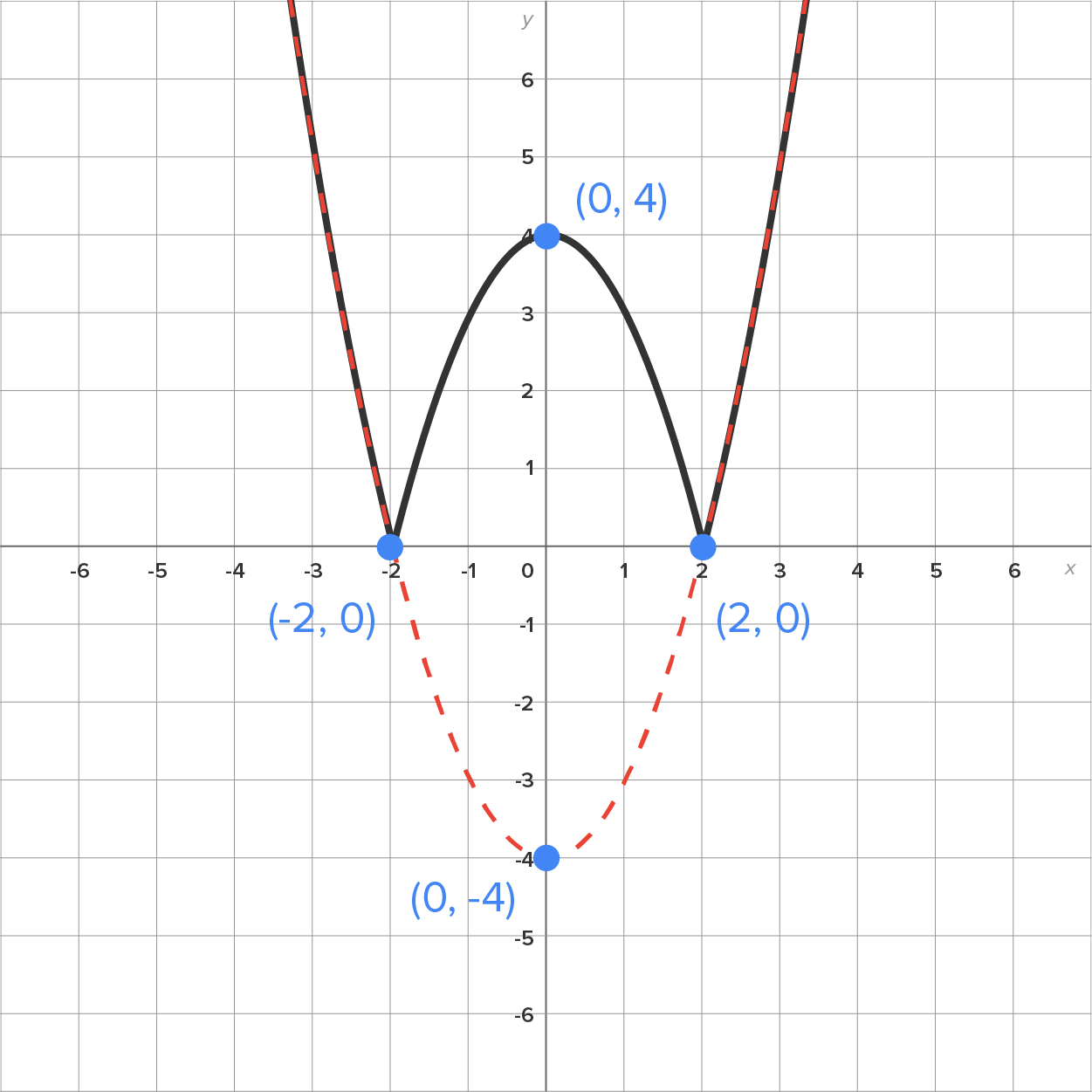
The graph of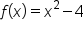 f open parentheses x close parentheses equals x squared minus 4 is shown below: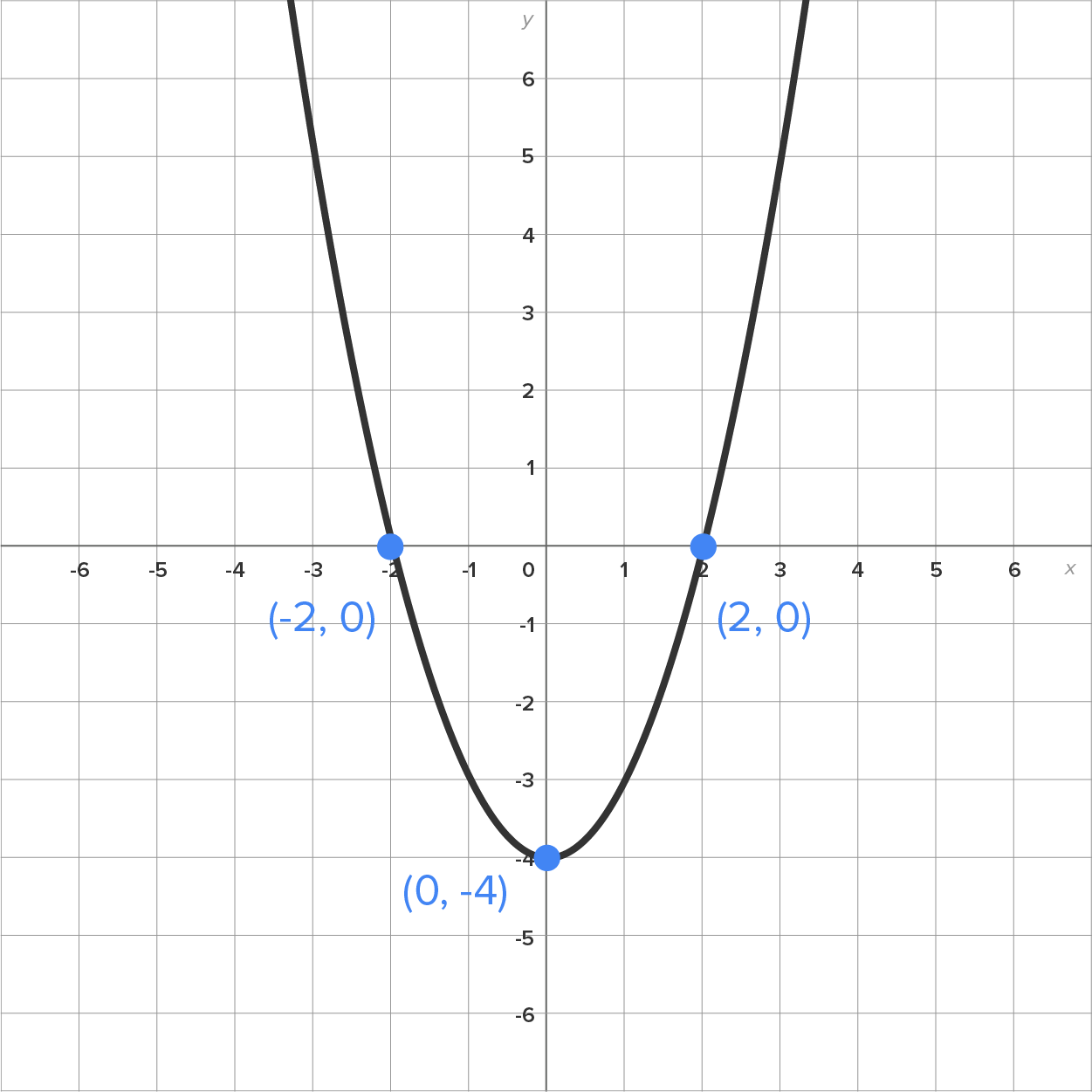

A graph with an x-axis and a y-axis ranging from −6 to 6, intersecting at the origin. The graph contains a parabolic curve opening upward, passing through the marked points (−2, 0), (0, −4), and (2, 0).

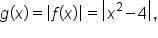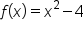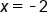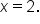To graph g open parentheses x close parentheses equals open vertical bar f open parentheses x close parentheses close vertical bar equals open vertical bar x squared minus 4 close vertical bar comma notice that the graph of f open parentheses x close parentheses equals x squared minus 4 is below the x-axis between x equals short dash 2 and x equals 2. This part reflects over the x-axis, while the rest of the graph remains the same.

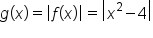On the left is the graph of g open parentheses x close parentheses equals open vertical bar f open parentheses x close parentheses close vertical bar equals open vertical bar x squared minus 4 close vertical bar with the graph of f open parentheses x close parentheses shown as a dashed line for comparison. On the right is the graph of g open parentheses x close parentheses equals open vertical bar x squared minus 4 close vertical bar.

A graph with an x-axis and a y-axis ranging from −6 to 6, intersecting at the origin. The graph contains two parabolic curves. The dashed parabolic curve starts in the third quadrant and opens upward, passing through the marked points (−2, 0), (0, −4), and (2, 0). The solid parabolic curve starts in the second quadrant and follows the dashed curve up to (−2, 0) but then opens downward, passing through the marked points (0, 4) and (2, 0). After reaching (2, 0), the solid curve traces the upward path of the dashed curve. 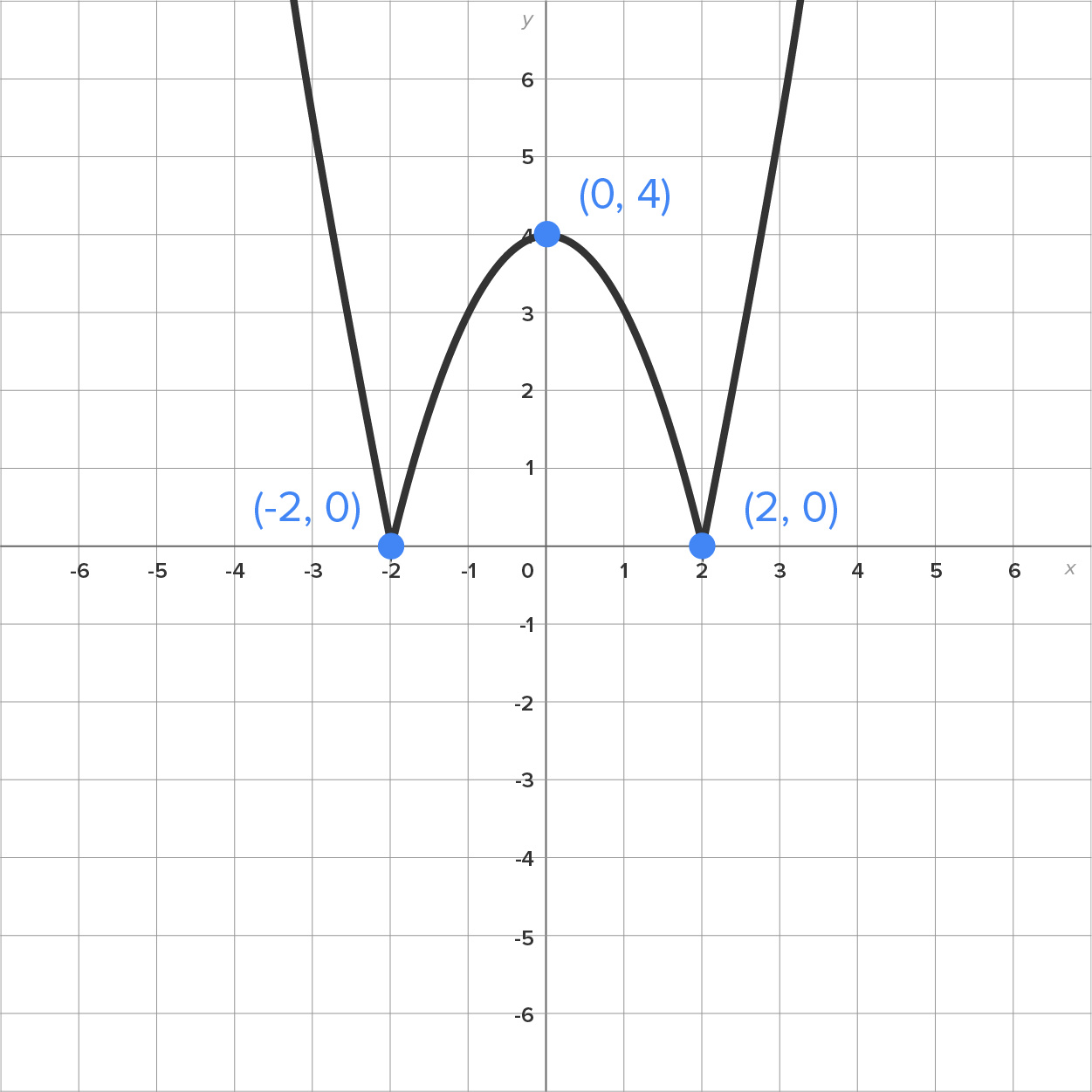A graph with an x-axis and a y-axis ranging from −6 to 6, intersecting at the origin. The graph contains a single solid parabolic curve with a W-like shape. The curve starts in the second quadrant and passes through the marked points (−2, 0), (0, 4), and (2, 0). The outer ends of the curve extend upward on both sides.

hint
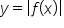To graph y equals open vertical bar f open parentheses x close parentheses close vertical bar given the graph of 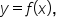y equals f open parentheses x close parentheses comma consider the following.
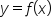  • The graphs are the same for all values of x where the graph of y equals f open parentheses x close parentheses is either below or above the x-axis.
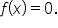
  • It may be helpful to locate the x-intercepts of the graph of f open parentheses x close parentheses first, since these are the points where f open parentheses x close parentheses equals 0.
  • The portion lying below the x-axis gets reflected over the x-axis.

EXAMPLE

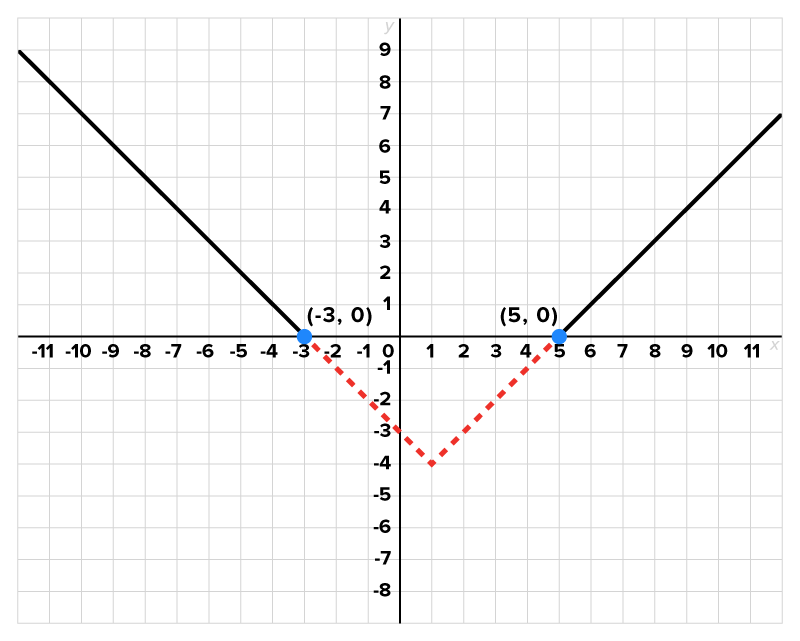
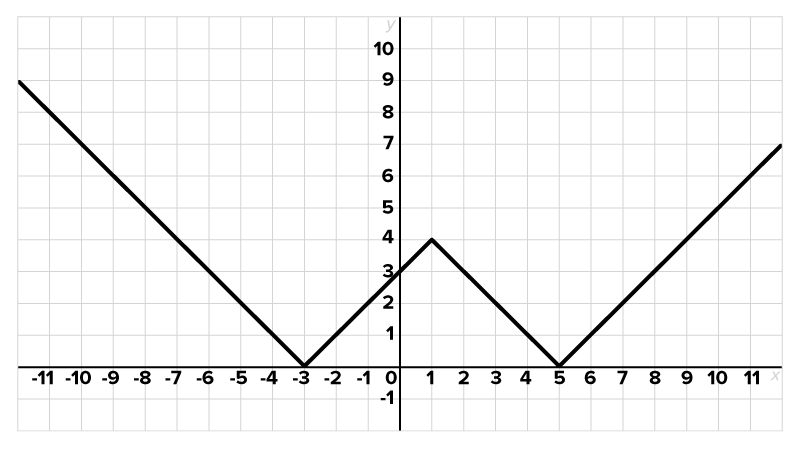
Consider the graph of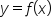 y equals f open parentheses x close parentheses shown below.

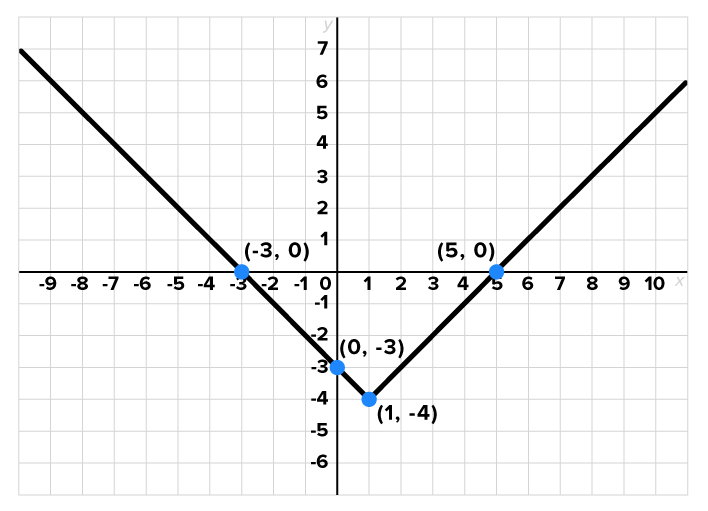
A graph with an x-axis ranging from −9 to 10 and a y-axis ranging from −6 to 7. A line slants downward from the second quadrant and passes through the marked points at (−3, 0) and (0, −3) till it reaches (1, −4). From here, it extends upward into the first quadrant by passing through the marked point at (5, 0) and forming a V-shape.

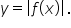
Use this graph to construct the graph of y equals open vertical bar f open parentheses x close parentheses close vertical bar.

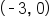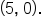First, note that the x-intercepts are open parentheses short dash 3 comma space 0 close parentheses and open parentheses 5 comma space 0 close parentheses. Since the graph is above the x-axis to the left of 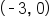open parentheses short dash 3 comma space 0 close parentheses and to the right of 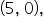open parentheses 5 comma space 0 close parentheses comma this portion of the graph will also be above the x-axis. The graph of f open parentheses x close parentheses is shown again below, this time with the portion below the x-axis dashed instead of solid. 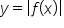This is the portion we need to focus on when graphing y equals open vertical bar f open parentheses x close parentheses close vertical bar.

A graph with an x-axis ranging from −11 to 11 and a y-axis ranging from −8 to 9. A solid line slants downward from the second quadrant to the marked point at (−3, 0). From here, the line continues as a dashed line and passes through the point (0, −3) until it reaches (1, −4). It then extends up to the marked point at (5, 0). From (5, 0), the line continues as a solid line, slanting upward into the first quadrant and forming a V-shape.

The dashed portion gets reflected over the x-axis.

This graph of y equals open vertical bar f open parentheses x close parentheses close vertical bar is shown below:

A graph with an x-axis ranging from −11 to 11 and a y-axis ranging from −1 to 10. A line slants downward from the second quadrant, passes through the points (−11, 8) and ends at (−3, 0). Then, another line segment starts at (-3, 0) and ands at (1, 4), followed by another segment that ends at (5, 0). The final line segment starts at (5, 0) and extends upward through the point (6, 1). The overall graph has a pointy W-shape.

try it
Consider the graph of y equals f open parentheses x close parentheses as shown below.
A graph with an x-axis and a y-axis ranging from −6 to 6, intersecting at the origin. The graph contains a cubic curve with an S-like shape. The curve rises from the third quadrant, reaches the point (−1, 0), extends to the point between 2 and 1 on the y-axis before falling through the point (2, 0), and rises again through the point (4, 0).

Sketch the graph of y = |f (x)|.
Any portion of the graph below the x-axis is reflected over the x-axis. This means that the portion to the left of x equals short dash 1 and between x equals 2 and x equals 4 are reflected over the x-axis; while the rest of the graph remains the same. The graph below shows the result.

A graph with an x-axis and a y-axis, ranging from −6 to 6 and intersecting at the origin. The graph contains a curve with a W-like shape. The curve descends from the upper part of the second quadrant till it reaches the point (−1, 0). From here, the curve takes a sharp turn to rise again, opens downward, passing between points 1 and 2 at the y-axis toward the point (2, 0); from this point, another curve opens downward toward the point (4, 0). After reaching (4, 0), the curve extends upward into the first quadrant.

summary
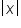In this lesson, you learned about the absolute value function of x, which represents the distance that a number x is from 0 on the number line. You learned about the piecewise definition of absolute value, given that in general, evaluating open vertical bar x close vertical bar requires two different rules, depending on what x is. It's important to remember that the absolute value function may look simple on the surface, but it has a more complicated definition beyond “turning things nonnegative.” You explored the graph of the basic absolute value function, applying rules you learned in a previous lesson to create graphs that illustrate the shifting, stretching, and reflecting of the basic absolute value function. Lastly, you learned about other absolute value graphs, noting that while the basic absolute function is simply a “V” shape, graphing 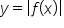y equals open vertical bar f open parentheses x close parentheses close vertical bar requires more thought and care.

SOURCE: THIS TUTORIAL HAS BEEN ADAPTED FROM CHAPTER 0 OF "CONTEMPORARY CALCULUS" BY DALE HOFFMAN. ACCESS FOR FREE AT WWW.CONTEMPORARYCALCULUS.COM. LICENSE: CREATIVE COMMONS ATTRIBUTION 3.0 UNITED STATES.

Terms to Know
Absolute Value

The distance that a number is from 0 on the number line.

© 2025 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC.